51. Модель освещения, используемая для построения реалистических изображений.

Большинство существующих формул закраски базируются на элементарных моделях освещения (например, точечный источник, рассеянный свет), которые позволяют выполнить достаточно быстрое построение реалистичных изображений, однако не позволяет добиться полной фотореалистичности.

Задачей модели Варна (David Warn, 1983) было моделирование реальной лаборатории фотохудожника (фото-студии), позволяющей использовать более сложные модели источников света. Базовое ядро таких моделей также основывается на точечной мо-

дели источника.

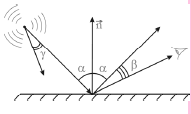
Направленный свет в модели Варна получается при помощи отражения света

точечного источника от идеальной отражающей поверхности. Направление на

источник и направление света при этом могут не совпадать (рис.6.8). Рис.6.8.

где IH - интенсивность направленного источника света; IU0 - интенсив-

ность базового источника света; γ - угол, который образует направление

на источник и направление света, исходящего из него; С - коэффициент

пространственной концентрации света

При увеличении величины С получаем источник света прожекторного типа (по аналогии с зависимостью, график которой приведен на рис.6.3). При уменьшении С, размер прожектора увеличивается и в пределе стремится к модели заливающего света.

Таким образом, формула закраски, с учетом присутствия в сцене направленного источника освещения, будет определяться следующей формулой:

Кроме описанного направленного источника света, модель Варна

включает в себя другие составные модели, которые имитируют заслонки

на источнике света и специальные отражающие экраны. Для моделиро-

вания луча прожектора, Варн предложил модель конуса, осью симмет-

рии которого является направление на источник света. При ___________помощи мо-

дели конуса можно получить четко ограниченное пятно света.

Конец 51 вопроса.

52.Модель освещения с учетом микрогеометрии поверхностей объектов.

Эта модель освещения в литературе носит название Торрэнса –Сперроу (Torrance K.E., Sparrow E.M., 1967). В модели Торрэнса –Сперроу в качестве источника света рассматривается телесный угол ω,противостоящий источнику. Связь между энергией источника (Еи ), падающей на единицу площади за единицу времени, и интенсивностью

света (Iи) определяется следующим образом:

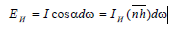
где α – угол падения, n – нормаль к поверхности, h – направление на ис-

точник света.Если поверхность представляет из себя не идеальную форму, а

форму имеющую хаотическое отклонение, то интенсивность отраженного от нее света должна быть меньше интенсивности падающего излучения. Интенсивность отраженного света I0 связывается с энергией источника Еи следующим образом:

где r – коэффициент двунаправленного отражения, определяющий до-

лю энергии отраженной в заданном направлении.Подставив (6.13) в (6.14), получим уравнение для I0 :

Кроме того, необходимо учесть, что коэффициент r зависит от двух составляющих светового потока: зеркального и диффузионного. Поэтому его представляют в виде следующей линейной комбинации:

где kд, kз – весовые коэффициенты, зависящие от характеристик поверхности.

Чтобы учесть эффект отражения рассеянного света в выражение (6.15) вводят дополнительную составляющую:

I = f kp rp ⋅ Ip (6.17)

где f – часть полусферы, открытая для источника; kр – весовой коэффициент, определяемый характеристиками поверхности; rр – коэффициент отражения рассеянного света, полученный путем интегрирования выражения (6.16) по всей полусфере; Iр – интенсивность рассеянного света.

Величины коэффициентов kд, kз, kр и значение Iр определяются экспериментальным путем. Значение же самих коэффициентов rд и rз можно вычислить используя законы и соотношения физической оптики.

На базе формул (6.13) - (6.17) можно получить следующую формулу закраски:

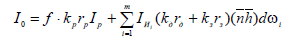
(6.18)

Эта модель называется моделью Торрэнса – Кука. Она позволяет учитывать не только наличие нескольких источников света, но и их разные размеры.

Основные сложности при вычислении выражения (6.18) вызывает расчет коэффициентов диффузной и зеркальной составляющих rд и rз.

Коэффициент диффузной составляющей rд зависит от угла падения α света на поверхность объекта. Однако на практике получается, что при величине ∠α < 70° значение rд мало отличается от значения коэффициента при нормальном отражении (∠α =0°). Поэтому в большинстве случаев зависимостью rд(α) можно пренебречь.

Коэффициент зеркальной составляющей rз, Он оказывает наибольшее влияние на видимый результат наибольшее влияние на видимый результат и зависит от многих параметров. В модели Торрэнса Сперроу рассматривается вычисление коэффициента rз на основании следующей формулы:

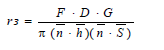
(6.19)

где F – коэффициент Френеля; D – функция распределения микрограней по поверхности объекта; G – коэффициент ослабления света за счет взаимозависимости граней; S – направление на наблюдателя.

Рассмотрим модель микрогеометрии поверхности, на которой базируется расчет освещенности по методу Торрэнса – Сперроу.

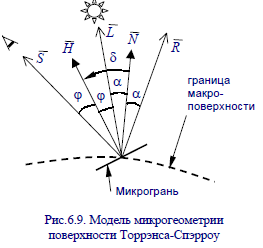
N – нормаль к макроповерхности,

H – нормаль микрограни,

R – направление отраженного света

S – направление света отраженного от микро грани

L – направление на источник света.

Чтобы была заметна зеркальная составляющая от микро грани необходимо, чтобы на-

правление S совпадало с направлением наблюдения.

Пусть n, h, l, s, r – единичные векторы соответствующих направлений, а α – угол падения и отражения для макро поверхности и δ – угол падения и отражения для микро грани.

Конец 52 вопроса.