Общие правила построения диаграммы Парето

1. Решить, какие проблемы (причины проблем) надлежит исследовать, какие данные собирать и как их классифицировать.

2. Разработать формы для регистрации исходных данных (например, контрольный листок).

3. Собрать данные, заполнив формы, и подсчитать итоги по каждому исследуемому фактору (показателю, признаку).

4. Для построения диаграммы Парето подготовить бланк таблицы, предусмотрев в нем графы для итогов по каждому проверяемому фактору в отдельности, накопленной суммы числа появлений соответствующего фактора, процентов к общему итогу и накопленных процентов.

5. Заполнить таблицу, расположив данные, полученные по проверяемому фактору, в порядке убывания значимости.

6. Подготовить оси (одну горизонтальную и две вертикальные линии) для постро-ения диаграммы. Нанести на левую ось ординат шкалу с интервалами от 0 до общей суммы числа выявленных факторов, а на правую ось ординат - шкалу с интервалами от 0 до 100, отражающую процентную меру фактора. Разделить ось абсцисс на интервалы в соответствии с числом исследуемых факторов или относительной частотой.

7. Построить столбиковую диаграмму. Высота столбца (откладывается по левой шкале) равна числу появлений соответствующего фактора. Столбцы располагают в порядке убывания (уменьшения значимости фактора). Последний столбец характеризует "прочие", т. е. малозначимые факторы, и может быть выше соседних.

8. Начертить кумулятивную кривую (кривую Парето) - ломаную, соединяющую точки накопленных сумм (количественной меры факторов или процентов). Каждую точку ставят над соответствующим столбцом столбиковой диаграммы, ориентируясь на его правую сторону.

9. Нанести на диаграмму все обозначения и надписи.

10. Провести анализ диаграммы Парето.

Примечание. Существуют и другие варианты построения диаграммы Парето.

Дополнительная информация:

• Пытайтесь достичь высоких результатов лишь по нескольким направлениям, а не повышать показатели по всем направлениям сразу.

• Концентрируйтесь только на ресурсах, приносящих наибольшую прибыль, не пытайтесь повысить эффективность всех ресурсов сразу.

• В каждой важной для вас области старайтесь определить, какие 20% усилий могут привести к 80% результатов.

• Максимально используйте те немногие удачные моменты, когда вы способны показать наивысшие результаты.

• Нехватка времени - миф. На самом деле времени у нас предостаточно. По-настоящему мы используем только 20% нашего дня. А многие талантливые люди делают основные "ходы" в течение нескольких минут.

Достоинства метода

Простота и наглядность делают возможным использование диаграммы Парето специалистами, не имеющими особой подготовки.

Сравнение диаграмм Парето, описывающих ситуацию до и после проведения улучшающих мероприятий, позволяют получить количественную оценку выигрыша от этих мероприятий.

Недостатки метода

При построении сложной, не всегда четко структурированной диаграммы возможны неправильные выводы.

№ 9 Случайные события и случайные величины. Вероятность. Теоремы сложения и умножения вероятностей

Основные определения. Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайное событие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина. Случайная величина является одним из центральных понятий теории вероятностей.Вероя́тность (вероятностная мера) — численная мера возможности наступления некоторого события.С практической точки зрения, вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений или опытов. Например, если среди встреченных на улице людей примерно половина — женщины, то можно говорить, что вероятность того, что встреченный на улице человек окажется женщиной, равна 1/2. Другими словами, оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента.Согласно определению П. Лапласа, мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель — число всех равновозможных случаев.

Теорема (сложения вероятностей). Вероятность суммы двух случайных событий равна сумме вероятностей этих событий минус вероятность их пересечения:

Теорема умножения вероятностей.

Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:

№ 10 Сбор и регистрация исходных статистических данных

Статистические данные должны быть адекватны:

объекту изучения;

времени, в которое они собираются и используются.

В данной главе описываются источники статистических данных, их виды и способы получения, а также приемы описания и представления количественных (числовых) и нечисловых данных.

Получение информации об объекте исследования является одной из основных составляющих статистического исследования. При статистическом исследовании следует руководствоваться целями и требованиями к результатам. Они определяют методы статистического анализа, исходя из которых организуется сбор исходных данных. В процессе статистического исследования следует опасаться следующих ошибок: нечетко сформулированных целей, некорректно примененных методов и ошибкок при получении исходных данных.

Получение исходных данных для статистического исследования может осуществляться двумя способами:

1) активный эксперимент, специально организованный для определения статистических зависимостей;

2) статистическое наблюдение.

Оба способа включают в той или иной мере следующие компоненты:

• факторы;

• процесс;

• отклики;

• план эксперимента;

• экспериментатор.

Виды статистических наблюдений можно классифицировать:

• по способу получения информации;

• по учету фактора времени;

• по полноте охвата совокупности.

Непосредственный учет, т.е. регистрация, — запись отдельных фактов.

Документальный учет основывается на данных различного рода документов. Типичным примером такого рода учета является бухгалтерский учет.

Различные формы опроса:

экспедиционная форма-обследование проводится специально выделенными регистраторами (лицо, проводящее опрос, само раздает и собирает анкеты);

саморегистрация (анкета)

корреспондентский опрос, при котором анкеты рассылаются и возвращаются по почте.

По учету фактора времени наблюдение можно классифицировать на:

• непрерывное (например, учет кадров);

• периодическое (бухгалтерская отчетность);

• единовременное, в случае потребности в информации, например, перепись населения.

Сводка видов и типов получения информации (статистических данных):

• учет фактора времени;

• непосредственный учет (регистрация, запись отдельных фактов);

• документальный учет;

• опрос;

• непрерывное получение;

• периодическое получение;

• единовременное получение;

• полнота охвата совокупности: сплошная, выборочная;

• экспедиционная форма;

• саморегистрация;

• корреспондентский опрос.

По полноте охвата статистической совокупности различают:

• несплошную, выборочную, когда обследуется не вся совокупность, а некоторая ее часть;

• сплошную, т.е. описание всех единиц совокупности;

• монографическую, когда подробно описываются типовые объекты.

  

№11 Гипергеометрическое распределение — это дискретное вероятностное распределение, которое описывает количество успехов в выборке без возвращений длины над конечной совокупностью объектов. Гипергеометрическое распределение описывает вероятность того, что именно дефектных в выборке из конкретных объектов, взятых из совокупности.

Дискретная случайная величина X имеет гипергеометрическое распределение, если она принимает значения 0, 1, 2, ..., min {n, M} с вероятностями

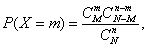
где m=1, 2, ..., min {n, M}, m≤N, n≤N; n, N, M - натуральные числа.

Гипергеометрическое распределение имеет случайная величина X=m - число объектов, обладающих данным свойством, среди n объектов , случайно извлечённых (без возврата) из совокупности N объектов, M из которых обладают этим свойством.

Гипергеометрическое распределение широко используется в практике статистического приёмочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочных обследований и некоторых других областях.

№12 Биноминальное распределение

Биноминальное распределение - распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p.

Это распределение интенсивно используется в картах контроля качества, p - доля годной продукции, q - доля брака.

Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p.

Биноминальное распределение относится к тем случаям контроля по атрибутивным (качественным, альтернативным) признакам, когда на выходе возможно лишь два исхода при независимых испытаниях: хорошо или плохо (принять или забраковать). Биноминальное распределение начинается с предположения об уровне брака в генеральной совокупности и определяет вероятность брака в выборке.

Числовые характеристики биноминального распределения:

М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;

D(m)=npq - дисперсия частоты появления события. А;

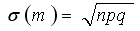- среднее квадратическое отклонение частоты.

№13 Распределение Пуассона

моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона - это дискретное распределение, являющееся одним из важных предельных случаев биномиального распределения. При росте n и зафиксированном значении произведения np=λ > 0 биномиальное распределение B(n,p) сходится к распределению Пуассона. Таким образом, случайная величина, имеющая распределение Пуассона с параметром λ, принимает неотрицательные целые значения с вероятностью

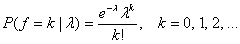
Интегральная функция вероятности распределения равна

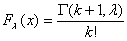
Параметр λ является одновременно и математическим ожиданием, и дисперсией случайной величины, имеющей распределение Пуассона.

Теорема. Математическое ожидание и дисперсия случайной величины X, распределённой по  закону Пуассона, совпадают и равны значению параметра этого закона, т. е.

При условии закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Наряду с "предельным" случаем биномиального распределения закон Пуассона может возникнуть и в ряде других случаев. Так для простейшего потока событий число событий, попадающих на произвольный отрезок времени, есть случайная величина, имеющая пуассоновское распределение. Также по закону Пуассона распределены, например, число рождения четверней, число сбоев на автоматической линии, число отказов сложной системы в "нормальном режиме", число "требований на обслуживание", поступивших в единицу времени в системах массового обслуживания, и др.

Замечание. Если случайная величина представляет собой сумму двух независимых случайных величин, распределённых по закону Пуассона, то она также распределена по закону Пуассона.

№14 Нормальный закон распределения

Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

            Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и , если её плотность вероятности f(x) имеет вид:

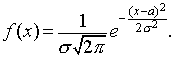
Кривая нормального распределения  f(x)  (нормальная кривая или кривая Гаусса) приведена на рисунке

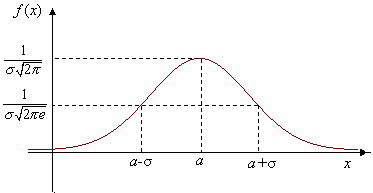
Теорема. Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а её дисперсия - квадрату параметра , т.е.

Рассмотрим влияние параметров нормального распределения на форму нормальной кривой. Если , и меняется параметр а, т.е. центр симметрии распределения, то кривая распределения будет смещаться вдоль оси абсцисс, не меняя формы (см. рисунок). Если a=const и меняется параметр , то меняется ордината максимума кривой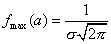 . При увеличении кривая распреде-ления становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении кривая вытягивается вверх, одновременно сжимаясь с боков (см. рисунок).

Нормальный закон распределения случайной величины с параметрами а=0 и   называется стандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.

№15 Распределе́ние Стью́дента

в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Другое название – T-распределение

Стьюдента распределение с f степенями свободы, распределение отношения Т = X/Y независимых случайных величин Х и Y, где Х подчиняется нормальному распределению  с математическим ожиданием EX = 0 и дисперсией DX = 1, а fY² имеет "Хи-квадрат" распределение с f степенями свободы.

Пусть — независимые стандартные нормальные случайные величины, такие что . Тогда распределение случайной величины , где

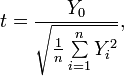
называется распределением Стьюдента с степенями свободы. Пишут . Её распределение абсолютно непрерывно и имеет плотность

,

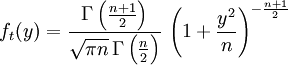где — гамма-функция Эйлера.

t-критерий Стьюдента - общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

t-критерий Стьюдента — общее название для статистических тестов, в которых статистика критерия имеет распределение Стьюдента. Наиболее часто t-критерии применяются для проверки равенства средних значений в двух выборках. Нулевая гипотеза предполагает, что средние равны (отрицание этого предположения называют гипотезой сдвига).

Все разновидности критерия Стьюдента являются параметрическими и основаны на дополнительном предположении о нормальности выборки данных. Поэтому перед применением критерия Стьюдента рекомендуется выполнить проверку нормальности. Если гипотеза нормальности отвергается, можно проверить другие распределения, если и они не подходят, то следует воспользоваться непараметрические статистические тесты.

16 С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. Это распределения Пирсона ("хи – квадрат"), Стьюдента и Фишера.

Распределении ("хи – квадрат"). Впервые это распределение было исследовано астрономом Ф.Хельмертом в 1876 году. В связи с гауссовской теорией ошибок он исследовал суммы квадратов n независимых стандартно нормально распределенных случайных величин. Позднее Карл Пирсон (Karl Pearson) дал имя данной функции распределения "хи – квадрат". И сейчас распределение носит его имя.

Благодаря тесной связи с нормальным распределением, Х²-распределение играет важную роль в теории вероятностей и математической статистике. Х²-распределение, и многие другие распределения, которые определяются посредством Х²-распределения (например - распределение Стьюдента), описывают выборочные распределения различных функций от нормально распределенных результатов наблюдений и используются для построения доверительных интервалов и статистических критериев.

Распределение Пирсона (хи - квадрат) – распределение случайной величины где X1, X2,…, Xn - нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение - единице.

Сумма квадратов

распределена по закону ("хи – квадрат").

При этом число слагаемых, т.е. n, называется "числом степеней свободы" распределения хи – квадрат. C увеличением числа степеней свободы распределение медленно приближается к нормальному.

Плотность этого распределения

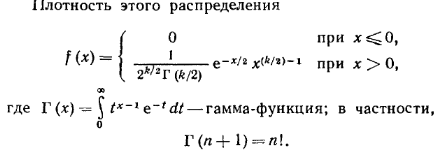
Итак, распределение Х² зависит от одного параметра n – числа степеней свободы.

Функция распределения Х² имеет вид:

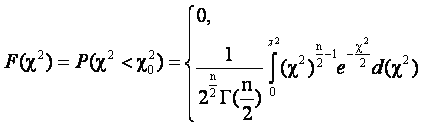
если ч2≥0. (2.7.)

На Рисунок 1 изображен график плотности вероятности и функции Х² – распределения для разных степеней свободы.

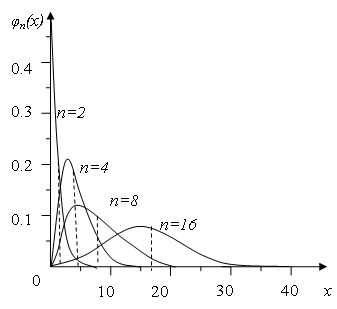
Рисунок 1 Зависимость плотности вероятности ц (x) в распределении Х² (хи – квадрат) при разном числе степеней свободы.

Моменты распределения "хи-квадрат":

M[ч2]=n

D[ч2]=2n

Распределение "хи-квадрат" используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.

№ 17 Точечная оценка предполагает нахождение единственной числовой величины, которая и принимается за значение параметра. Такую оценку целесообразно определять в тех случаях, когда объем ЭД достаточно велик. Причем не существует единого понятия о достаточном объеме ЭД, его значение зависит от вида оцениваемого параметра (к этому вопросу предстоит вернуться при изучении методов интервальной оценки параметров, а предварительно будем считать достаточной выборку, содержащую не менее чем 10 значений). При малом объеме ЭД точечные оценки могут значительно отличаться от истинных значений параметров, что делает их непригодными для использования.

Задача точечной оценки параметров в типовом варианте постановки состоит в следующем [3].

Имеется: выборка наблюдений (x₁, x₂, …, x_n) за случайной величиной Х. Объем выборки n фиксирован.

Известен вид закона распределения величины Х, например, в форме плотности распределения f(T, x), где T – неизвестный (в общем случае векторный) параметр распределения. Параметр является неслучайной величиной.

Требуется найти оценку  параметра T закона распределения.

Ограничения: выборка представительная.

Существует несколько методов решения задачи точечной оценки параметров, наиболее употребительными из них являются методы максимального (наибольшего) правдоподобия, моментов и квантилей.