9. Формула полной вероятности

Формула полной вероятности. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B₁ B₂, ..., В_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероят­ность события А: Р(А) = Р (B₁) P_B1 (А) + Р (В₂) Р_В2, (A) + ... ... + Р(В_п)Р_Вп(А).

Эту формулу называют «формулой полной вероятности». Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий B₁ B₂, ..., В_n . Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В₁А, B₂A, ..., В_nА. Пользуясь для вычисления вероятности события А теоремой сложе­ния, получим Р(А) = Р (В₁А) + Р (В₂А) +...+Р (В_nА). (*)

Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем Р (В₁А); Р (В₂А) = Р (B₂) P_B2 (А); ... ; Р(В_пА) = Р(В_n)Р_Вп(А).

Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности Р(А) = Р (В₁) P_B1 (А)+ Р (В₂) P_B2 (А)) + ... ...+Р(В_п)Р_Вп(А).

ИЛИ: Если E=H1+H2+…+Hn,HiHk=,i≠k, то p(A)= .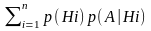

10. Вероятность гипотез. Формулы Бейеса

Пусть событие А может наступить при условии появления одного из несовместных событий В₁, В₂, . . ., Вn, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

Р(А) = Р (B₁) P_B1 (А) + Р (В2) P_B2 (А)+......+Р(Вn)Р_Вn(А).(*)

Допустим, что произведет испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности Pa (В1), P_A(B2),+ … Р_А(Вn).

Найдем сначала условную вероятность Р_А (B1). По теореме умножения имеем

Р (AB₁) = Р (А) Р_А (В₁) = Р (В1) P_B1 (A). Отсюда P_A(B₁)=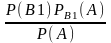

Заменив здесь Р (А) по формуле (*), получим

P_A(B₁)= .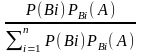

Полученные формулы называются формулами Бейеса. Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

11. Формула Бернулли

Схема независимых испытаний. Формула Бернулли. Если производится несколько испытаний, при­чем вероятность события А в каждом испытании не за­висит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.

Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных собы­тий, которые называют простыми.

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q=1—р.

Поставим перед собой задачу вычислить вероятность того, что при п испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится п—k раз. Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно k раз в определенной последовательности. Например, если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события: ААА , АА А, А АА, ААА. Запись ААА означает, что в первом, втором и третьем испытаниях событие А наступило, а в четвертом испытании оно не появилось, т. е. наступило противоположное событие А; соответственный смысл имеют и другие записи.

Искомую вероятность обозначим Р_n (k). Например, символ Р₅ (3) означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.

Поставленную задачу можно решить с помощью так называемой формулы Бернулли.

Вывод формулы Бернулли. Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит п—k раз, по теореме умножения вероятностей независимых событий равна p^kq^n-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из п элементов по k элементам, т. е. . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в п испытаниях) равна вероятности одного сложного события, умноженной на их число: P_n(k)= p^kq^n-k или P_n(k)= p^kq^n-k. Полученную формулу называют формулой Бернулли.