- •1. События и операции над ними
- •2. Классическое определение вероятности
- •3. Статистическое определение вероятности
- •4. Геометрическое определение вероятности
- •5. Теорема сложения вероятностей
- •6. Произведение событий
- •7. Условная вероятность
- •8. Теорема сложения вероятностей совместных событий
- •9. Формула полной вероятности
- •10. Вероятность гипотез. Формулы Бейеса
- •11. Формула Бернулли
- •12. Локальная теорема Лапласа
- •13. Интегральная теорема Лапласа
- •14. Дискретные и непрерывные случайные величины
- •15. Закон распределения вероятностей дискретной случайной величины.
- •16. Биномиальное распределение
- •17. Распределение Пуассона
- •18. Геометрическое распределение
- •19. Гипергеометрическое распределение
- •20. Математические операции над случайными величинами
- •21. Числовые характеристики дискретных случайных величин
- •22. Математическое ожидание дискретной случайной Величины
- •23. Вероятностный смысл математического ожидания
- •24. Свойства математического ожидания
- •25. Отклонение случайной величины от ее математического ожидания
- •26. Дисперсия дискретной случайной величины
- •27. Формула для вычисления дисперсии
- •28. Свойства дисперсии
- •29. Среднее квадратическое отклонение
- •30. Начальные и центральные теоретические моменты
- •31. Закон больших чисел
- •32. Функция распределения случайной величины
- •33. Непрерывные случайные величины. Плотность вероятности
- •34. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс
- •35. Моменты непрерывной случайной величины
- •36. Равномерный закон распределения
- •37. Показательный (экспоненциальный) закон распределения
- •38. Нормальный закон распределения
- •39. Вероятность попадания в заданный интервал нормальной случайной величины
- •40. Вычисление вероятности заданного отклонения
- •41. Распределение "хи квадрат"
- •42. Распределение Стьюдента
- •43. Система двух случайных величин
- •1. Генеральная и выборочная совокупности
- •2. Повторная и бесповторная выборки. Репрезентативная выборка
- •3. Способы отбора из генеральной совокупности.
- •4. Статистическое распределение выборки.
- •5. Эмпирическая функция распределения.
- •6. Полигон и гистограмма.
- •7. Статистические оценки параметров распределения.
- •8. Несмещенные, эффективные и состоятельные оценки.
- •9. Средние значения количественного признака X.
- •10. Дисперсии количественного признака X.
- •11. Оценка генеральной дисперсии по исправленной выборочной.
- •12. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
- •13. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ.
- •14. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ.
- •15. Доверительные интервалы для оценки среднего квадратического отклонения σ нормального распределения.
- •16. Статистическая проверка статистических гипотез.
- •17. Отыскание правосторонней критической области.
- •18. Отыскание левосторонней и двусторонней критических областей.
34. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс
М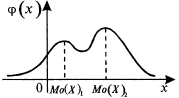 ода
Мо(Х) случ. величины X - наз-ся ее наиболее
вероятное значение (для которого вер-сть
рi или плотность вер-сти φ(х) достигает
max).
Если вер-сть или плотность достигает
max
в неск точках, распредел-е наз-тся
полимодальным.
Медиана
Ме(Х) непрерывной случ. величины X
наз-тся такое ее значение, для которого
Р(X<Me(X))=P(X>Me(X))=0,5, т.е. вер-сть того, что
X примет значение, < Ме(Х) или > ее,
одна и та же и = 0,5. Геометрически:
вертикальная прямая, проходящая через
точку х=Ме(Х), делит площадь фигуры под
кривой распределения на 2 равные части.
Квантилем
уровня q
наз-ся такое значение Xq
случ/ величины, при котором ф-я ее
распред-я принимает значение, равное
q, т.е. F(Xq)
= P(X<xq) = q. Ме – это квантиль уровня 0,5.
Начальным
моментом k-го порядка
случ. велич X наз-ся мат. ожидание k-й
степени этой величины: νk=M(X^k).
Для непрерывн случ велич: νk=∫х^k
φ(x)dx
(интеграл от -∞ до +∞). Центральный
моментом k-го
порядка случ. велич. X наз-тся матю
ожидание k-й
степени отклонения X от ее мат. ожидания:
μk=M[X-M(X)]^k.
Для непрерывной случ велич: μk=
∫(х-М(Х))^k
φ(x)dx
(интеграл от -∞ до +∞). Третий центральный
момент μ3 служит для характер-ки
асимметрии
распределения. А= μ3\σ^3. Если распред-е
симметрично относительно мат. ожидания,
то А=0. Эксцесс
Е= μ4\ σ^4 – 3.
ода
Мо(Х) случ. величины X - наз-ся ее наиболее
вероятное значение (для которого вер-сть
рi или плотность вер-сти φ(х) достигает
max).
Если вер-сть или плотность достигает
max
в неск точках, распредел-е наз-тся
полимодальным.
Медиана
Ме(Х) непрерывной случ. величины X
наз-тся такое ее значение, для которого
Р(X<Me(X))=P(X>Me(X))=0,5, т.е. вер-сть того, что
X примет значение, < Ме(Х) или > ее,
одна и та же и = 0,5. Геометрически:
вертикальная прямая, проходящая через
точку х=Ме(Х), делит площадь фигуры под
кривой распределения на 2 равные части.
Квантилем
уровня q
наз-ся такое значение Xq
случ/ величины, при котором ф-я ее
распред-я принимает значение, равное
q, т.е. F(Xq)
= P(X<xq) = q. Ме – это квантиль уровня 0,5.
Начальным
моментом k-го порядка
случ. велич X наз-ся мат. ожидание k-й
степени этой величины: νk=M(X^k).
Для непрерывн случ велич: νk=∫х^k
φ(x)dx
(интеграл от -∞ до +∞). Центральный
моментом k-го
порядка случ. велич. X наз-тся матю
ожидание k-й
степени отклонения X от ее мат. ожидания:
μk=M[X-M(X)]^k.
Для непрерывной случ велич: μk=
∫(х-М(Х))^k
φ(x)dx
(интеграл от -∞ до +∞). Третий центральный
момент μ3 служит для характер-ки
асимметрии
распределения. А= μ3\σ^3. Если распред-е
симметрично относительно мат. ожидания,
то А=0. Эксцесс
Е= μ4\ σ^4 – 3.
35. Моменты непрерывной случайной величины
Определение. Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Хk.
![]()
![]()
Для дискретной случайной величины: .
 Для
непрерывной случайной величины: .
Для
непрерывной случайной величины: .
Начальный момент первого порядка равен математическому ожиданию.
 Определение.
Центральным моментом порядка
k
случайной величины Х называется
математическое ожидание величины
Определение.
Центральным моментом порядка
k
случайной величины Х называется
математическое ожидание величины
![]()
![]()
 Для
дискретной случайной величины: .
Для
дискретной случайной величины: .
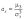 Для
непрерывной случайной величины: .
Для
непрерывной случайной величины: .
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии.
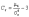 Определение.
Для
характеристики островершинности и
плосковершинности распределения
используется величина, называемая
эксцессом.
Определение.
Для
характеристики островершинности и
плосковершинности распределения
используется величина, называемая
эксцессом.
Кроме рассмотренных величин используются также так называемые абсолютные моменты:
Абсолютный
начальный момент:
 .
.
Абсолютный
центральный момент:
 .
.
Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.
36. Равномерный закон распределения
Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
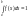 или
или
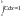 .
Отсюда,
.
Отсюда,
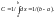 Итак искомая плотность вероятности
равномерного распределения:
Итак искомая плотность вероятности
равномерного распределения: