
- •1. События и операции над ними
- •2. Классическое определение вероятности
- •3. Статистическое определение вероятности
- •4. Геометрическое определение вероятности
- •5. Теорема сложения вероятностей
- •6. Произведение событий
- •7. Условная вероятность
- •8. Теорема сложения вероятностей совместных событий
- •9. Формула полной вероятности
- •10. Вероятность гипотез. Формулы Бейеса
- •11. Формула Бернулли
- •12. Локальная теорема Лапласа
- •13. Интегральная теорема Лапласа
- •14. Дискретные и непрерывные случайные величины
- •15. Закон распределения вероятностей дискретной случайной величины.
- •16. Биномиальное распределение
- •17. Распределение Пуассона
- •18. Геометрическое распределение
- •19. Гипергеометрическое распределение
- •20. Математические операции над случайными величинами
- •21. Числовые характеристики дискретных случайных величин
- •22. Математическое ожидание дискретной случайной Величины
- •23. Вероятностный смысл математического ожидания
- •24. Свойства математического ожидания
- •25. Отклонение случайной величины от ее математического ожидания
- •26. Дисперсия дискретной случайной величины
- •27. Формула для вычисления дисперсии
- •28. Свойства дисперсии
- •29. Среднее квадратическое отклонение
- •30. Начальные и центральные теоретические моменты
- •31. Закон больших чисел
- •32. Функция распределения случайной величины
- •33. Непрерывные случайные величины. Плотность вероятности
- •34. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс
- •35. Моменты непрерывной случайной величины
- •36. Равномерный закон распределения
- •37. Показательный (экспоненциальный) закон распределения
- •38. Нормальный закон распределения
- •39. Вероятность попадания в заданный интервал нормальной случайной величины
- •40. Вычисление вероятности заданного отклонения
- •41. Распределение "хи квадрат"
- •42. Распределение Стьюдента
- •43. Система двух случайных величин
- •1. Генеральная и выборочная совокупности
- •2. Повторная и бесповторная выборки. Репрезентативная выборка
- •3. Способы отбора из генеральной совокупности.
- •4. Статистическое распределение выборки.
- •5. Эмпирическая функция распределения.
- •6. Полигон и гистограмма.
- •7. Статистические оценки параметров распределения.
- •8. Несмещенные, эффективные и состоятельные оценки.
- •9. Средние значения количественного признака X.
- •10. Дисперсии количественного признака X.
- •11. Оценка генеральной дисперсии по исправленной выборочной.
- •12. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
- •13. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ.
- •14. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ.
- •15. Доверительные интервалы для оценки среднего квадратического отклонения σ нормального распределения.
- •16. Статистическая проверка статистических гипотез.
- •17. Отыскание правосторонней критической области.
- •18. Отыскание левосторонней и двусторонней критических областей.
37. Показательный (экспоненциальный) закон распределения
Показательны (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью:
 ,
где
,
где
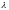 -
постоянная положительная величина.
-
постоянная положительная величина.
Найдем математическое ожидание:
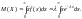 Интегрируя
по частям, получим:
Интегрируя
по частям, получим:
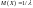 .
.
Найдем дисперсию:
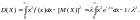 Интегрирую
по частям, получим
Интегрирую
по частям, получим
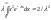 ,
следовательно
,
следовательно
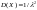 .
.
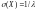 .=>
Математическое ожидание и средне
квадратическое отклонение показательного
распределения равны между собой.
.=>
Математическое ожидание и средне
квадратическое отклонение показательного
распределения равны между собой.

38. Нормальный закон распределения
Нормальным
называют распределение вероятностей
непрерывной случайной величины, которое
описывается плотностью
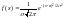 .
Это распределение определяется двумя
параметрами
.
Это распределение определяется двумя
параметрами
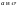 .
Достаточно знать эти параметры, чтобы
задать нормальное распределение.
.
Достаточно знать эти параметры, чтобы
задать нормальное распределение.
 есть
математическое ожидание, а
есть
математическое ожидание, а
 -
средне квадратическое отклонение
нормального распределения.
-
средне квадратическое отклонение
нормального распределения.
Нормированным
называют нормальное распределение с
параметрами
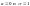 .
.
Плотность нормированного распределения
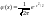 .
.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
39. Вероятность попадания в заданный интервал нормальной случайной величины
Известно, что если случайная величина X задана плотностью распределения F(x), то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:
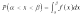 .
.
Пусть случайная величина X распределена по нормальному закону. Тогда
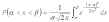 .
.
Преобразуем
эту формулу так, чтобы можно было
пользоваться готовыми таблицами. Введем
новую переменную
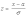 .
Отсюда
.
Отсюда
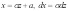 .
.
Найдем
новые пределы интегрирования. Если x
=
a,
то
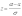 ,
если x
= b,
то
,
если x
= b,
то
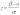 .
Тогда
.
Тогда
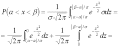
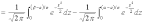 .
.
Выражение
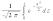 ,
входящее в эту формулу, является функцией
верхнего предела X, которая называется
функцией Лапласа или интегралом
вероятностей и обозначается Ф(x). В
результате получаем:
,
входящее в эту формулу, является функцией
верхнего предела X, которая называется
функцией Лапласа или интегралом
вероятностей и обозначается Ф(x). В
результате получаем:
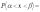 Ф
Ф
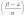 —
Ф
—
Ф
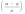 ,
,
где
Ф(x) =
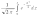 .
.
Эту формулу называют формулой Лапласа.
Если
случайная величина X является признаком
генеральной совокупности, то формула
Лапласа дает долю элементов генеральной
совокупности, у которых значение
признака X находится в границах от
![]() до
до
![]() .
.
Интеграл,
через который выражается функция
Лапласа, нельзя выразить через
элементарные функции. Его можно
представить в виде степенного ряда,
если разложить в ряд подынтегральную
функцию
 и
почленно проинтегрировать ряд. Тогда
и
почленно проинтегрировать ряд. Тогда
Ф(x) =
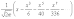 .
.
C помощью этого ряда можно вычислить значение Ф(x) для любого x с любой точностью. Составлены специальные таблицы значений функции Лапласа.
Отметим ряд свойств функции Лапласа, полезных для применения.
1. Функция Ф(x) – нечетная, т. е. Ф(-x) = –Ф(x).
2. Функция Ф(x) – возрастающая, быстро приближающаяся к своему пределу, равному 0,5: Ф(0) = 0, Ф(1) = 0,3413, Ф(2) = 0,4772, Ф(3) = 0,4986, Ф(4) = 0,4999 и т.д. На практике полагают Ф(x)= 0,5 для x>5.
40. Вычисление вероятности заданного отклонения
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х по абсолютной величине меньше заданного положительного числа d, т. е. требуется найти вероятность осуществления неравенства |x —а|<d.
Заменим это неравенство равносильным ему двойным неравенством

Тогда получим:

Приняв во внимание равенство:
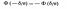
(функция Лапласа—нечетная), окончательно имеем
Вероятность заданного отклонения равна
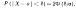
Eсли две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d,d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s .
 Пример.
Случайная величина Х распределена
нормально. Математическое ожидание и
среднее квадратическое отклонение Х
соответственно равны 20 и 10. Найти
вероятность того, что отклонение по
абсолютной величине будет меньше трех.
Пример.
Случайная величина Х распределена
нормально. Математическое ожидание и
среднее квадратическое отклонение Х
соответственно равны 20 и 10. Найти
вероятность того, что отклонение по
абсолютной величине будет меньше трех.
Решение: Воспользуемся формулой

По условию ,
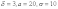 тогда
тогда

