8. Несмещенные, эффективные и состоятельные оценки.

Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.

Пусть Θ∗ - статистическая оценка неизвестного параметра Θ теоретического распределения. Допустим, что по выборке объема n найдена оценка Θ∗

1. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку Θ∗

2. Повторяя опыт многократно, получим числа Θ∗ 1,Θ∗ 2, . . . ,Θ∗ k,, которые, вообще говоря, различны между собой. Таким образом, оценку Θ∗, можно рассматривать как случайную величину, а числа Θ∗1,Θ∗2, . . . ,Θ∗ k, - как ее возможные значения. Представим, что оценка Θ∗ дает приближенное значение Θ с избытком; тогда каждое найденное по данным выборок число Θ∗ i (i = 1, 2, . . . , k больше истинного значения Θ. Ясно, что в этом случае и математическое ожидание (среднее значение) случайной величины Θ∗ больше, чем Θ, т. е. M[Θ∗] > Θ. Если Θ∗ дает оценку с недостатком, то M[Θ∗] < Θ.

Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. По этой причине естественно потребовать, чтобы математическое ожидание оценки Θ∗ было равно оцениваемому параметру. Хотя соблюдение этого требования не устранит ошибок (одни значения Θ∗ больше, а другие меньше Θ), однако ошибки разных знаков будут встречаться одинаково часто. Иными словами, соблюдение требований M[Θ∗] = Θ гарантирует от получения систематических ошибок.

Определение. Несмещенной называют статистическую оценку Θ∗, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме выборки, т. е. M[Θ∗] = Θ

В теории ошибок измерений систематическими ошибками называют неслучайные ошибки, искажающие результаты измерений в одну определенную сторону. Например, измерение длины растянутой рулеткой систематически дает заниженные результаты.

Определение. Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Определение. Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

Определение. Состоятельной называют статистическую оценку, которая при n → ∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n → ∞ стремится к нулю, то такая оценка будет и состоятельной.

9. Средние значения количественного признака X.

Генеральная средняя: Пусть изучается дискретная генеральная совокупность относительно количественного признака X.

Определение. Генеральной средней xΓ называют среднее арифметическое значений признака генеральной совокупности.

Если все значения x1, x2, . . . , xN признака генеральной совокупности объема N различны, то

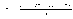
Если же значения признака x1, x2, . . . , xk имеют соответственно частоты N1,N2, . . . ,Nk, причем N1 + N2 + . . . + Nk = N, то

т. е. генеральная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.

Пусть генеральная совокупность объема N содержит объекты с различными значениями признака X, равными x1, x2, . . . , xN. Пусть из этой совокупности наудачу извлекается один объект. Вероятность того, что будет извлечен объект со значением признака, например x1, равна 1 \N . С этой же вероятностью может

быть извлечен и любой другой объект. Таким образом, величину признака X можно рассматривать как случайную величину, возможные значения которой x1, x2, . . . , xN имеют одинаковые вероятности, равные 1\N . Найдем математическое ожидание M[X]:

Если рассматривать признак X генеральной совокупности как случайную величину, то математическое ожидание признака равно генеральной средней этого признака:

Этот вывод получили, считая, что все объекты генеральной совокупности имеют различные значения признака. Такой же итог будет получен, если допустить, что генеральная совокупность содержит по несколько объектов с одинаковым значением признака. Обобщая полученный результат на генеральную совокупность с непрерывным распределением признака X, и в этом случае определим генеральную среднюю как математическое ожидание признака:

Выборочная средняя

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.

Определение. Выборочной средней xB называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x1, x2, . . . , xn признака выборки объема n различны, то

Если же значения признака x1, x2, . . . , xk имеют соответственно частоты n1, n2, . . . , nk, причем n1 + n2 + . . . + nk = n, то

или

т. е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.

Выборочная средняя, найденная по данным одной выборки - это определенное число. Если извлекать другие выборки того же объема из той же генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке. Таким образом, выборочную среднюю можно рассматривать как случайную величину, и можно говорить о распределениях (теоретическом и эмпирическом) выборочной средней и о числовых характеристиках этого распределения (его называют выборочным), в частности о математическом ожидании и дисперсии выборочного распределения.

Определение. Групповой средней называется среднее арифметическое значений признака, принадлежащих группе.

Теперь целесообразно ввести специальный термин для средней всей совокупности.

Определение. Общей средней x называется среднее арифметическое значений признака, принадлежащих всей совокупности.