1.2. Частные производные, градиент функции n переменных.

Определение 1.3. Производная функции f(x₁,x₂) по переменной x₁ при фиксированной второй переменной x₂ называется частной производной функции f(x₁,x₂) по переменной x_1, что символически записывается так:

или , или просто .

Аналогично определяется первая частная производная функции f(x₁,x₂) по переменной x_2.

Если в точке (x₁⁰,x₂⁰) значение частной производной функции f(x₁,x₂) по переменной x₁ (x₂) положительно, то есть, если ,

, то при малом росте переменной x₁ (x₂) относительно x₁⁰ (x₂⁰) при фиксированной переменной x₂ (x₁) значение функции y растет, то есть из того, что первая частная производная по переменной положительна, следует свойство монотонности функции по этой переменной.

Примеры вычисления частных производных функций.

Пример1. Дана функция y=a₀x₁^a1x₂^a2. Требуется вычислить частные производные по обеим переменным.

;

Пример 2. Имеем y=a₀+a₁x₁+a₂x₂, тогда , . При нахождении частной производной слагаемое a₂x₂ фиксировано, то есть играет роль постоянной, как и a_0, поэтому производная от них по x₁ равна нулю. Аналогично для переменной x₂.

Определение 1.4. Упорядоченная пара первых частных производных 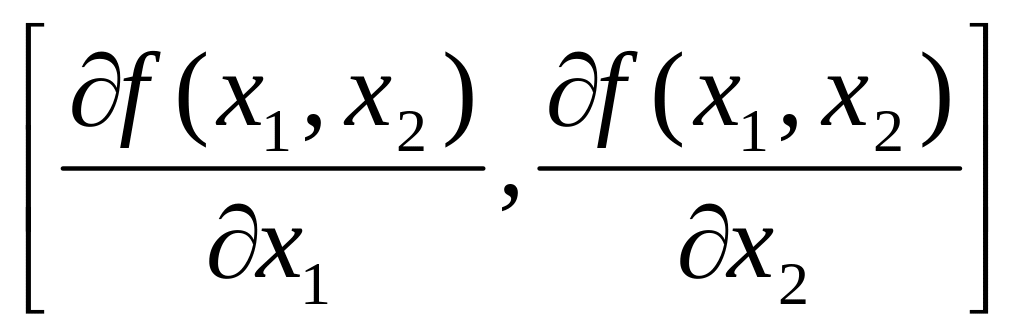функции f(x₁,x₂) называется градиентом функции и обозначается grad f(x₁,x₂).

Градиент функции в точке (x₁⁰,x₂⁰) показывает направление самого быстрого роста функции в этой точке.

2. Элементы теории экстремума.

Определение 1.5. Точка (x₁⁰,x₂⁰) называется точкой локального максимума (минимума) функции f(x₁,x₂) двух переменных x₁ и x₂, если для всех точек (x₁,x₂) из области определения функции f,близких точке (x₁⁰,x₂⁰), справедливо неравенство f(x₁⁰,x₂⁰)≥f(x₁,x₂) (f(x₁⁰,x₂⁰)≤f(x₁,x₂)).

Само частное значение f(x₁⁰,x₂⁰) называется локальным максимумом (локальным минимумом) функции f(x₁,x₂).

Отметим, что вместо двух терминов (максимума и минимума) используют один термин экстремум.

На графиках функций в трехмерном пространстве около точек локального экстремума графики функций имеют вид «шапочки» или перевернутой «шапочки».

Определение 1.6. Точка (x₁⁰,x₂⁰) называется точкой глобального максимума (минимума) функции f(x₁,x₂) двух переменных x₁ и x₂, если для всех точек (x₁,x₂) из области определения функции f справедливо неравенство f(x₁⁰,x₂⁰)≥f(x₁,x₂) (f(x₁⁰,x₂⁰)≤f(x₁,x₂)).

Само частное значение f(x₁⁰,x₂⁰) называется глобальным максимумом (глобальным минимумом) функции f(x₁,x₂).

Если функция f(x₁,x₂) выпукла вниз и имеет локальный минимум, то он является глобальным минимумом. Если функция f(x₁,x₂) выпукла вверх и имеет локальный максимум, то он является глобальным максимумом.

Необходимое условие локального экстремума формулируется следующим образом.

Пусть функция y=f(x₁,x₂) в точке (x₁⁰,x₂⁰) имеет локальный экстремум (точка (x₁⁰,x₂⁰) - внутренняя для области определения функции y=f(x₁,x₂)), тогда

Точки, удовлетворяющие этой системе ограничений, называются критическими точками функции f.

2. Модели потребительского выбора.

2.1. Функция полезности.

Будем считать, что потребитель располагает доходом I, который он полностью тратит на приобретение благ (продуктов). Точнее говоря, величина I - это не доход, а расход данного потребителя. Потребитель решает статическую задачу, то есть в модели не учитываются его межвременные предпочтения и возможности делать или расходовать сбережения. Цены благ считаются заданными. Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определенные количества благ, и математическая модель такого его поведения называется моделью потребительского выбора. Вначале мы рассмотрим модель с двумя видами благ. Такая модель удобна, прежде всего, возможностью графической интерпретации, сохраняя при этом все принципиальные свойства общей модели. Рассмотрим потребительские наборы из двух благ. Потребительский набор (для краткости набор) - это вектор (x₁,x₂) координата x₁ которого равна количеству единиц первого блага, а координата x₂ равна количеству единиц второго блага.

Выбор потребителя характеризуется отношением предпочтения, суть которого состоит в следующем. Считается, что потребитель про каждые 2 набора может сказать, что: либо один из них более желателен, чем другой, либо потребитель не видит между ними разницы. Отношение предпочтения транзитивно, т.е. если набор A=(a₁,а₂) предпочтительнее набора B=(b₁,b₂), а набор B предпочтительнее набора C=(c₁,c₂), то набор А предпочтительнее набора С.

На множестве потребительских наборов (x₁,x₂) определена функция u(x₁,x₂), называемая функцией полезности потребителя. Частное значение u(x₁,x₂) на потребительском наборе (x₁,x₂) равно потребительской оценке, которую имеет индивидуум для этого набора. Потребительскую оценку u(x₁,x₂) набора (x₁,x₂) принято называть уровнем (или степенью) удовлетворения потребностей индивидуума, если он приобретает или потребляет данный набор (x₁,x₂). Каждый потребитель имеет, вообще говоря, свою функцию полезности. Если набор А предпочтительнее набора В, то u(А)>u(В).

Функция полезности удовлетворяет следующим свойствам:

1. Возрастание потребления одного продукта при постоянном потреблении другого продукта ведет к росту потребительской оценки, т.е.

если x₁² > x₁¹, то u(x₁²,x₂)>u(x₁¹,x₂);

если x₂² > x₂¹, то u(x₁,x₂²)>u(x₁,x₂¹).

Это свойство называется свойством ненасыщения.

1¹. Пусть первые частные производные u по x₁ и x₂ положительны, т.е.

Из свойства 1' следует свойство 1.

Первые частные производные называются предельными пoлезностями продуктов: u'_x1 называется предельной полезностью первого продукта, u'_x2- предельная полезность второго продукта. Для предельных полезностей первого и второго продуктов используется также символика Mu₁, Mu₂.

2. Предельная полезность каждого продукта уменьшается, если объем его потребления растет. Это свойство предельной полезности называется законом убывания предельной полезности.

2'. Пусть

вторые частные производные отрицательны.

Из свойства 2' следует свойство 2.

3. Предельная полезность каждого продукта увеличивается, если растет количество другого продукта. В этом случае продукт, количество которого фиксировано, оказывается относительно дефицитным. Поэтому дополнительная его единица приобретает большую ценность и может быть потреблена более эффективно. Данное свойство не столь очевидно, как 1-2, и справедливо не для всех благ: если блага могут полностью замещать друг друга в потреблении, свойство 3 не выполняется. Предположение 3 вводится не всегда, но оно гарантирует выпуклость вниз линий безразличия.

3'. Пусть

 (вторые смешанные производные положительны)

Из свойства 3' следует свойство 3.

Линия, соединяющая потребительские наборы (x₁,x₂), имеющие один и тот же уровень удовлетворения потребностей индивидуума,  называется линией безразличия. Линия безразличия есть не что иное, как линия уровня функции полезности. Множество линий безразличия называется картой линий безразличия. На рис.4 показан фрагмент карты линий безразличия. Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются. Если линия безразличия L_t расположена выше и правее ("северо-восточнее") линии безразличия L_p, то t>p . Верно и обратное. Иными словами чем "северо-восточнее" расположена линия безразличия, тем большему уровню удовлетворения потребности она соответствует. Условия 1-3 означают, что линия безразличия убывает (является нисходящей) и строго выпукла к началу координат (к точке 0).

Рис.4

Важной характеристикой функции полезности является предельная норма замещения.

Определение. Предельная норма замещения показывает количество единиц товара j, которое пользователь готов заменить единицей товара i. Обозначается:

Примеры.

1. Пусть U(x₁,x₂)=10x₁^1/2x₂^1/2. Проверим, выполняются ли для этой функции свойства, которым должна удовлетворять функция полезности.

при x₁>0, x₂>0

при x₁>0, x₂>0

Таким образом, свойство не насыщения (положительны первые частные производные) выполняется.

 

Отрицательность вторых частных производных показывает, что полезность прирастает убывающим темпом, а линии безразличия выпуклы к началу координат.

Из выполнения этих условий следует, что функция U(x₁,x₂)=10x₁^1/2x₂^1/2 может использоваться как функция полезности.

2. Линия уровня  имеет уравнение: =10x₁^1/2x₂^1/2 , тогда ²=100x₁x₂ и x₂=²/100x₁, т.е. кривые безразличия представляют гиперболы в первой четверти плоскости, которые при увеличении   расположены северо-восточнее.

3. Для функции полезности U(x₁,x₂)=10x₁^1/2x₂^1/2 вычислить предельную полезность при наборе товаров x₁=25, x₂=9.

Предельная полезность товара x₁ равна:

 

Предельная полезность товара x₂ равна:

 

4. Для функции полезности U(x₁,x₂)=10x₁^1/2x₂^1/2 вычислить предельную норму замещения первого товара вторым при наборе товаров x₁=25, x₂=9.