5.1. Оптимизация прибыли в долговременном промежутке.

Задача оптимизации прибыли в долговременном промежутке математически записывается следующим образом:

PR→max при х₁≥0,x₂≥0.

В случае долговременного промежутка фирма свободно может выбирать любой вектор затрат.

Как правило F(х₁,0)=F(0,x₂)=0, то есть при отсутствии хотя бы одного ресурса выпуска нет, поэтому можно считать, что х₁>0,x₂>0.

Математически эта задача на глобальный абсолютный максимум. Из математического анализа следует, что точки глобального максимума следует искать среди тех, которые удовлетворяют системе уравнений (необходимое условия экстремума функции в точке):

; или учитывая, что

PR=C₀∙F(х₁,x₂)-с₁х₁₊с₂x₂ :

или

Из свойств производственной функции (выпуклость) следует, что локальный экстремум является глобальным. Набор (х₁^*,x₂^*) затрат ресурсов, удовлетворяющий системе, называется локальным рыночным равновесием фирмы в долговременном промежутке. Подставим вектор (х₁^*,x₂^*) в уравнения, получим тождества:

.

Поделим первое тождество на второе, получим: ,

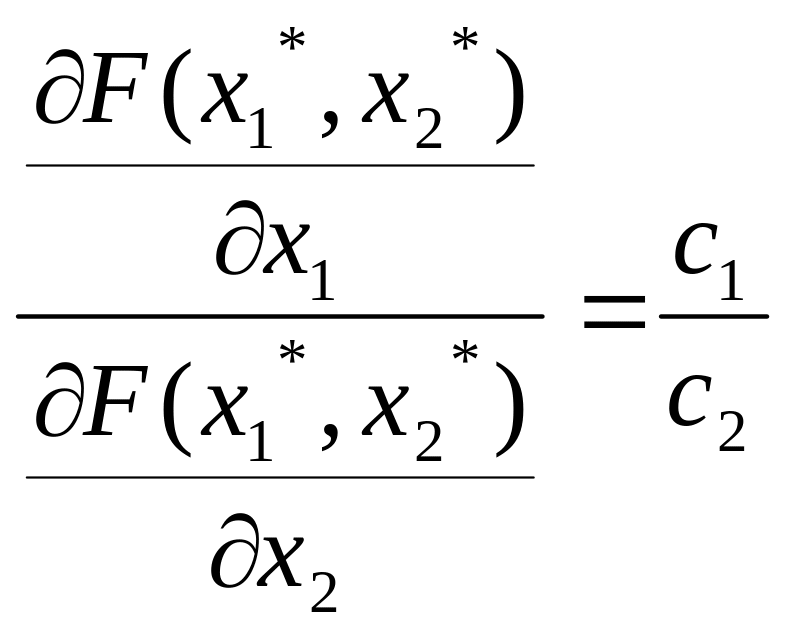то есть в точке локального рыночного равновесия фирмы отношение предельных производительностей ресурсов равно отношению их рыночных цен. Эта дробь называется предельной нормой замещения первого ресурса вторым.

Приведем геометрическую интерпретацию решения задачи. Для этого проведем через точку (х₁^*,x₂^*) изокванту и изокосту (линия уровня функции затрат). Уравнение изокванты имеет вид F(х₁,x₂)= F(х₁^*,x₂^*)=Y^*. Уравнение изокосты имеет вид с₁х₁₊с₂x₂₌С⁰, где С⁰= с₁х₁^*₊с₂x₂^*_. Тангенс угла наклона касательной к изокванте совпадает с тангенсом угла наклона изокосты в точке локального рыночного равновесия, то есть касательная к изокванте совпадает с изокостой, то есть в точке локального рыночного равновесия фирмы изокванта и изокоста касаются.

Рис.9.

5.2. Задача максимизации объема выпуска при ограничении на ресурсы.

Для долговременного промежутка рассмотрим задачу:

F(х_1,x₂)→max

при условиях с₁х₁₊с₂x₂≤V, (5.1.)

х₁≥0,x₂≥0.

Решение этой задачи математического программирования можно изобразить геометрически.

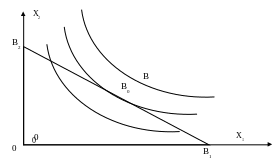
Рис.10.

Решение (х₁^*(V),x₂^*(V)) обращает ограничение (5.1) в равенство с₁х₁^*₊с₂x₂^*=V, поэтому можно рассматривать задачу:

F(х_1,x₂)→max

при условии с₁х₁₊с₂x₂=V; х₁≥0,x₂≥0.

Задачи разные, но решение у них одно и то же.

Решим эту задачу формально с помощью метода Лагранжа. Функция Лагранжа будет иметь вид: . Вычислим первые частные производные функции Лагранжа по всем переменным, приравняем их нулю и решим систему уравнений:

, ,

или в развернутом виде:

, , =0.

Решение задачи – «укороченная» критическая точка функции Лагранжа (х₁^*(V),x₂^*(V)).

При решении предыдущей задачи были определены издержки производства в точке локального рыночного равновесия фирмы С⁰= с₁х₁^*₊с₂x₂^*. Если в ограничении рассматриваемой задачи положить V=C⁰, то можно несложно показать, что , то есть величина обратная множителю Лагранжа, равна рыночной цене единицы продукции фирмы.