
- •1. Случайные события и действия над ними.
- •2. Алгебра событий.
- •3. Вероятность события. Свойства вероятности.
- •4. Теорема сложения вероятностей.
- •5. Условная вероятность.
- •6. Теорема умножения вероятностей. Независимые события.
- •7. Формула полной вероятности. Теорема Байеса.
- •8. Случайная величина. Определение. Пример.
- •9. Функция распределения случайной величины.
- •10. Свойства функции распределения.
- •11. Случайные величины дискретного типа.
- •12. Математическое ожидание дискретной случайной величины. Свойства математического ожидания.
- •13. Дисперсия дискретной случайной величины. Свойство дисперсии.
- •14. Производящая функция дискретной случайной величины.
- •15. Формулы для математического ожидания и дисперсии дискретной случайной величины через производящую функцию.
- •16. Схемы испытаний Бернулли.
- •17. Биномиальное распределение.
- •18. Математическое ожидание, дисперсия и производящая функция биномиальной случайной величины.
- •19. Мода биномиального распределения.
- •20. Распределение Пуассона.
- •21. Предельная теорема Пуассона.
- •22. Локальная предельная теорема Муавра-Лапласа.
- •23. Интегральная предельная теорема Муавра-Лапласа.
- •24. Дифференциальная и интегральная функции Гаусса.
- •25. Закон больших чисел в схеме Бернулли.
- •26. Непрерывные случайные величины. Свойство плотности распределении.
- •27. Равномерное распределение.
- •28. Нормальное распределение.
- •29. Показательное распределение.
- •31. Мода непрерывной случайной величины.
- •32. Медиана непрерывной случайной величины.
- •33. Математическое ожидание непрерывной случайной величины. Свойства математического ожидания.
- •39. Двумерные непрерывные случайные величины.
- •40. Числовые характеристики системы двух случайных величин.
- •41. Коэффициент ковариации и его свойства.
- •42. Коэффициент корреляции и его свойства.
- •43. Виды сходимости последовательности случайных величин.
- •44. Неравенство Чебышева.
- •45. Закон больших чисел для сумм независимых случайных величин.
- •46. Центральная предельная теорема теории вероятности.
- •47. Метод наименьших квадратов
- •48. Линейная среднеквадратическая регрессия
- •49. Генеральная совокупность. Случайная выборка. Вариационный ряд.
- •50. Эмпирическая функция распределения. Теорема Гливенко.
- •51. Выборочное среднее значение и выборочная дисперсия. Сходимость к теоретическим значениям.
- •52. Выборочный коэффициент ковариации.
- •53. Выборочный коэффициент корреляции.
- •54. Доверительные интервалы для неизвестного математического ожидания нормального распределения.
- •55. Критерий x2.
- •5 6. Понятие случайного процесса. Определение и примеры
- •57. Марковские процессы. Переходные вероятности
- •58. Теорема Колмогорова-Чепмена для переходных вероятностей
- •59. Дифференциальные уравнения Колмогорова для переходных вероятностей
- •60. Уравнения Колмогорова в стационарных режимах
24. Дифференциальная и интегральная функции Гаусса.
Когда npq>9: Теорема: предположим, что 0<p<1, тогда xk=(k-np)/npq; |xk|<=C=const. pn(k)=Cnkpkqn-k; n: pn(k)=(1/2)(1/npq)e (1+n(k)); |n(k)|<=C/n; Пусть (x)=(1/2)e , тогда pn(k)(1/npq)(xk). Ф-ция (x) назыв. дифференц. ф-цией Гаусса: (x)=(1/2)e . pn(k1,k2)=k=k1k2pn(k).
Теорема: n – Бернулиевская случ. величина, n{0,1,2,…,n}; p{n=k}=pn(k); En=np; Dn=npq; =Dn=npq; Пусть -<a<=b<, тогда при n вер-ть того, что a<=(n-np/npq)<=b стремится к: (1/2)abe dx=ab(x)dx, т.е.: p{a<=(n-np/npq)<=b}(1/2)abe dx=ab(x)dx. Ф(x)=(1/2)-xe dt=-x(t)dt, где Ф(x) – интегральная ф-ция Гаусса. (x)=Ф’(x)(производная от интегр. ф-ции). Выразим ab(x)dx через Ф(x): график интегр. ф-ции Гаусса:
ab(x)dx=-b(x)dx--a(x)dx=Ф(b)-Ф(a). Интегральная теорема Муавра-Лапласа может быть записана так (через интегральную ф-цию Гаусса): Ф(b)-Ф(а). p{a<(n-np/npq)<=b}Ф(b)-Ф(а). Применим теорему к вычислению суммы: p{k1<=n<=k2}=k=k1k2Cnkpkqn-k=p{(k1-np/npq)<= (n-np/npq)<= (k2-np/npq)}Ф((k2-np/npq))-Ф((k1-np/npq)). Значения интегральной ф-ции Гаусса (дифференц. ф-ции Гаусса) при всех допустимых значениях аргумента X можно найти в любом учебнике по теорверу.
25. Закон больших чисел в схеме Бернулли.
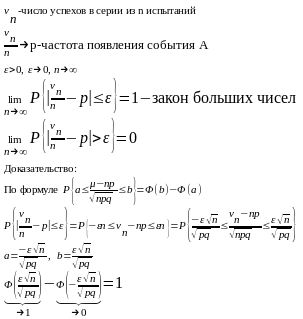
26. Непрерывные случайные величины. Свойство плотности распределении.
Плотность распределения (плотность вероятности) f(x) непрерывной случайной величины Х называется производная ее функции распределения:
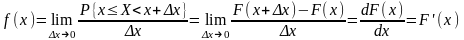
Основные св-ва плотности распределения:
1. Плотность распределения неотрицательна: f(x)>=0
2. Условие нормировки: -+f(x)dx=1
3. Вероятность попадания случайной величины Х на произволдьный участок [a,b[ равна: p{a<=X<b}=abf(x)dx
4. Функция распределения F(x) случайной величины Х выражается через ее плотность: F(x)=p{X<x}=p{-<X<x}=-xf(x)dx
27. Равномерное распределение.
Непрерывная СВ Х имеет равномерное распределение, если ее плотность вероятности в некотором интервале [a,b] постоянна, т.е. если все значения Х в этом интервале равновероятны:
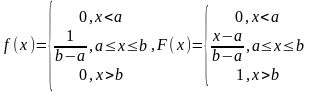
Числовые хар-ки равномерно распределенной СВ: mX=(a+b)/2; DX=(b-a)2/12
28. Нормальное распределение.
Непрерывная СВ Х имеет нормальное распределение, если е плотность вероятности и функция распределения равны:
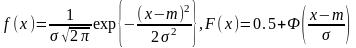 ,
где m,
– параметры распределения (>0),
,
где m,
– параметры распределения (>0),
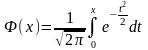 - ф-ция Лапласа.
- ф-ция Лапласа.
Значения функции Лапласа приведены в специальной таблице. При использовании таблицы значений ф-ции Лапласа учитывать, что Ф(-x) = -Ф(x), Ф(0)=0, Ф()=0.5.
Числовые хар-ки нормальной СВ:
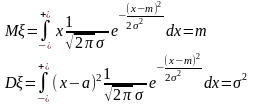
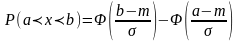
29. Показательное распределение.
Показательным
(экспонтециальным) называют распределение
вер-тей непрерывной случайной величины
Х, кот. описывается плотностью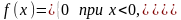 ,где
-постоянная
положительная величина. Видно, что
показат. распредел. определ. одним
параметром .
Найдем ф-цию распределения показательного
закона:
,где
-постоянная
положительная величина. Видно, что
показат. распредел. определ. одним
параметром .
Найдем ф-цию распределения показательного
закона: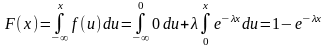 Итак:
Итак:
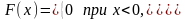 .
Графики плотности и функции распределения
.
Графики плотности и функции распределения
 показательного
закона:
показательного
закона:
Найдем вер-ть попадания в интервал (а,b) непрерывной случайной величины Х, кот-ая распределна по показательному закону, задонному ф-ией распределения: F(x)=1-e-x(x0). Используем формулу Р(аХ b)=F(b)-F(a). Учитывая, что F(a)= 1-F(b)= 1-e-b, получим: Р(аХ b)= e-а- e-b. Значение ф-ии e-х находится по таблице.
Числовые
хар-ки показательного распределения:
Пусть непрерывная случ величина Х
распределена по показательному закону:
.Найдем
математическое
ожидание.
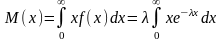 .
Интегрируя по частям, получим М(Х)=1/.
Т.О.математическое ожидане показат.
распределения равно обратной величине
парам-ра .
Найдем Дисперсию
.
Интегрируя по частям, получим М(Х)=1/.
Т.О.математическое ожидане показат.
распределения равно обратной величине
парам-ра .
Найдем Дисперсию
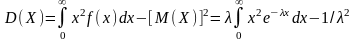 .
Интегрируя по частям, получим
.
Интегрируя по частям, получим
 ,следовательно
D(X)=1/2.
Найдем среднеквадратическое отклонение
для чего извлечем квадратный корень
из дисперсии: (Х)=1/2.математич
ожидание и среднее квадратич отклонение
показат распределения равны между
собой.
,следовательно
D(X)=1/2.
Найдем среднеквадратическое отклонение
для чего извлечем квадратный корень
из дисперсии: (Х)=1/2.математич
ожидание и среднее квадратич отклонение
показат распределения равны между
собой.
30. Распределение Коши.!!! Случайная величина имеет распределение Коши с параметрами a и c, если ее функция распределения и функция плотности вероятностей имеют соответственно вид:
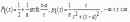
У распределения Коши не существует ни математического ожидания, ни дисперсии. Это распределение не имеет ни одного момента положительного порядка.
