52. Выборочный коэффициент ковариации.

(X,Y) – двумерная совокупность, {(x₁,y₁), (x₂,y₂),…,(x_n,y_n)} – n-мерная выборка из двумерной совокуп-ти {X,Y}, (x₁,y₁) – 1 наблюдение и т.д. F(x,y)=p{X<x; Y<y}; EX=m_x; EY=m_y; _x²=E(x-m_x)²; _y²=E(x-m_y)²; cov(x,y)=E(x-m_x)(y-m_y); r_XY=cov(X,Y)/(_x_y). Выборочным коэффициентом ковариации C_n(X,Y) назыв. величина, кот. определяется по ф-ле: C_n(X,Y)=(1/n)_j=1ⁿ(x_j- )(y_j-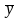 ); =(1/n)(x₁+x₂+…+x_n); =(1/n)(y₁+y₂+…+y_n). З-н больших чисел для C_n(X,Y): p{|cov(X,Y)-C_n(X,Y)|>}0, >0, n.

53. Выборочный коэффициент корреляции.

(X,Y) – двумерная совокупность, {(x₁,y₁), (x₂,y₂),…,(x_n,y_n)} – n-мерная выборка из двумерной совокуп-ти {X,Y}, (x₁,y₁) – 1 наблюдение и т.д. F(x,y)=p{X<x; Y<y}; EX=m_x; EY=m_y; _x²=E(x-m_x)²; _y²=E(x-m_y)²; cov(x,y)=E(x-m_x)(y-m_y); r_XY=cov(X,Y)/(_x_y). Выборочным коэффициентом корреля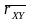ции , назыв. величина, кот. определ. по следующей ф-ле: =C_n(X,Y)/S_XS_Y. S_X²=(1/n)_j=1ⁿ(x_j- )²; S_Y²=(1/n)_j=1ⁿ(y_j- )².  r_XY (используется для оценки), где r_XY – теоретич. коэффициент корреляции.

54. Доверительные интервалы для неизвестного математического ожидания нормального распределения.

Метод доверительных интервалов: X, F_x(x)=F_x(x,), где  - неизвестн., x₁,x₂,…,x_n – выборка объема n. Как по выборке оценить пар-р ? Если сущ. 2 статистики: T₁=T₁(x₁,x₂,…,x₃), T₂=T₂(x₁,x₂,…,x_n), такие, что T₁<T₂, и при любом : 0<=<=1 выполняется условие: p{T₁<=<=T₂}>=, то мы говорим, что неизвестный пар-р [T₁,T₂] с коэффициентом доверия . На практике =0,95. Если оказыв., что с вер-тью =0,95 [T₁,T₂], то говорят, что этому интервалу можно доверять с вер-тью 0,95. Интервальная оценка. Пример: F_x(x,)=(1/(2))_-^+e dt; =(m,). Строим доверит. интервал для m в обоих случаях: 1. m-неизвестн.,  - известн.; 2. m – неизвестн.,  - неизвестн. 1) 0<<1; =0,95, Ф(_)=, где _ вычисляется по табл., Ф(x) – ф-ция распределения стандартн. нормального з-на, тогда p{ -_ (/n)<=m<= +_ (/n)}=. Доверительный интервал: [ -_ (/n)(лев. граница интервала), +_ (/n)(правая граница)] => Теорема доверит. интерв. для неизвестного среднего значения m нормального з-на при известной дисперсии . 2) доверит. интерв. для неизвестного m в случае неизвестн. дисперсии . Задаем : 0<<1, на практике =(<)0,95. Находим по табл. квантиль нормального з-на f(x) _ (квантилью порядка p непрерыв. с.в. x с ф-цией распределения F_x(x), назыв. число x_p, кот. удовлетворяет ур-ю F_x(x_p)=p, кот. назыв. квантильным ур-ем.): Ф(_)=, тогда утверждается, что вер-ть: p{ -_( /n)<=m<= +_( /n)}=. [ -_( /n), +_( /n)] – доверит. интервал, где =((1/(n-1))_j=1ⁿ(x_j- )²); E ²=².

55. Критерий x2.

A₁, ..., A_m - m возможных исходов некоторого опыта; p₁, ..., p_m - вероятности cooтветствующих исходов, _i=1^mp_i=1; n - число независимых повторений опыта;

₁, ..., _m - число появлений соответствующих исходов в n опытах, _i=1^mv_i=n; p₁⁰, ..., p_m⁰ - гипотетические значения вероятностей, p_i⁰ 0, _i=1^mp_i⁰=1. Требуется по наблюдениям ₁,...,_m проверить гипотезу Н о том , что вероятности p₁, ..., p_m имеют значения p₁⁰, ..., p_m⁰, т.е.

Н: p_i= p_i⁰ , i=1, ...,m. Оценками для p₁, ..., p_m являются 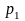= ₁ /n, ..., = _m/n. Мерой расхождения между гипотетическими и эмпирическими вероятностями принимается величина

,

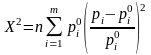к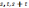 оторая с точностью до множителя n есть усредненное с весами p_i⁰ значение квадрата относительного отклонения значений от p_i⁰. Статистика X² называется статистикой хи-квадрат Пирсона. Для ее вычисления используются две формулы (1):

Условно статистику можно записать так:

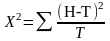
Н - наблюдаемые частоты _i, Т - теоретические (ожидаемые) частоты np_i⁰. Поскольку по закону больших чисел  p_i при n  , то

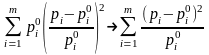(1.1)

Последняя величина равна 0, если верна Н; если же Н не верна, то X²  . Процедура проверки гипотезы состоит в том, что если величина X² приняла “слишком большое” значение, т.е. если X²  h (2), то гипотеза Н отклоняется; если это не так, будем говорить, что наблюдения не противоречат гипотезе.

Пусть X₁, X₂, X_n- независимые случайные величины, каждый из кот. имеет стандартное нормальное распределение P{x_i<x}=Ф(x); X²_n= X²₁+ X²₂+ X²_n. Функция распределения с.в. F X²_n(x)=P{x_i<x}. Плотность: f X_n² (x)=F’ X_n²(r), тогда f X_n² (x)- назыв. X_n² функцией. Г(x)=₀^e^-tt^x-1dt - известная гамма функция.

f X_n² (x)= (1/(2^((n/2)-1)Г(n/2)))e^-(x/2)x^((n/2)-1), число n называется степенью свободы.

С хема применения критерия: 1.Определяется мера расхождения X² по формуле 1.1 2.Определяется число степеней свободы. как число разрядов I минус s-число наложенных связей. 3.по n и . X² определяется вероятность того, что величина, имеющая распределение X² с n степенями свободы, превзойдет данное значение X².Если эта вероятность весьма мала, гипотеза отбрасывается как неправдоподобная. Если вероятность велика, гипотезу можно признать не противоречащей опытным данным.