
- •1. Случайные события и действия над ними.
- •2. Алгебра событий.
- •3. Вероятность события. Свойства вероятности.
- •4. Теорема сложения вероятностей.
- •5. Условная вероятность.
- •6. Теорема умножения вероятностей. Независимые события.
- •7. Формула полной вероятности. Теорема Байеса.
- •8. Случайная величина. Определение. Пример.
- •9. Функция распределения случайной величины.
- •10. Свойства функции распределения.
- •11. Случайные величины дискретного типа.
- •12. Математическое ожидание дискретной случайной величины. Свойства математического ожидания.
- •13. Дисперсия дискретной случайной величины. Свойство дисперсии.
- •14. Производящая функция дискретной случайной величины.
- •15. Формулы для математического ожидания и дисперсии дискретной случайной величины через производящую функцию.
- •16. Схемы испытаний Бернулли.
- •17. Биномиальное распределение.
- •18. Математическое ожидание, дисперсия и производящая функция биномиальной случайной величины.
- •19. Мода биномиального распределения.
- •20. Распределение Пуассона.
- •21. Предельная теорема Пуассона.
- •22. Локальная предельная теорема Муавра-Лапласа.
- •23. Интегральная предельная теорема Муавра-Лапласа.
- •24. Дифференциальная и интегральная функции Гаусса.
- •25. Закон больших чисел в схеме Бернулли.
- •26. Непрерывные случайные величины. Свойство плотности распределении.
- •27. Равномерное распределение.
- •28. Нормальное распределение.
- •29. Показательное распределение.
- •31. Мода непрерывной случайной величины.
- •32. Медиана непрерывной случайной величины.
- •33. Математическое ожидание непрерывной случайной величины. Свойства математического ожидания.
- •39. Двумерные непрерывные случайные величины.
- •40. Числовые характеристики системы двух случайных величин.
- •41. Коэффициент ковариации и его свойства.
- •42. Коэффициент корреляции и его свойства.
- •43. Виды сходимости последовательности случайных величин.
- •44. Неравенство Чебышева.
- •45. Закон больших чисел для сумм независимых случайных величин.
- •46. Центральная предельная теорема теории вероятности.
- •47. Метод наименьших квадратов
- •48. Линейная среднеквадратическая регрессия
- •49. Генеральная совокупность. Случайная выборка. Вариационный ряд.
- •50. Эмпирическая функция распределения. Теорема Гливенко.
- •51. Выборочное среднее значение и выборочная дисперсия. Сходимость к теоретическим значениям.
- •52. Выборочный коэффициент ковариации.
- •53. Выборочный коэффициент корреляции.
- •54. Доверительные интервалы для неизвестного математического ожидания нормального распределения.
- •55. Критерий x2.
- •5 6. Понятие случайного процесса. Определение и примеры
- •57. Марковские процессы. Переходные вероятности
- •58. Теорема Колмогорова-Чепмена для переходных вероятностей
- •59. Дифференциальные уравнения Колмогорова для переходных вероятностей
- •60. Уравнения Колмогорова в стационарных режимах
44. Неравенство Чебышева.
З-н
больших чисел:
Sn=x1+x2+…+xn
– сумма;
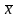 =(1/n)Sn
– среднее значение суммы; mi=EXi,
i=1,2,…,n;
=(1/n)Sn
– среднее значение суммы; mi=EXi,
i=1,2,…,n;
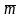 =(1/n)(m1+m2+…+mn)
– среднее знач. мат.ожид.;
-
случайное среднее,
-
неслучайное. Пос-ть с.в. {xn}
при n
удовлетвор. з-ну больших чисел, если
для любого достаточно малого числа
(>0)
выполняется соотношение:
limnp{|
-
|<=}=1(*)
– сходимость по вер-ти, |
-
|
- разность будет сколь угодно мала =>
E
=
.
Перепишем соотношение (*) иначе:
p{|
-
|<=}+p{|
-
|>}=1,
[|
-
|<=]-А,
[|
-
|<]-
(
A=).
p{|
-
|>}=1-p{|
-
|<=},
limnp{|
-
|>}0
(**). Условия для случ. величин x1,x2,…,xn,
для кот. выполняется з-н больших чисел.
Теорема
Маркова:
последов-ть с.в. x1,x2,…,xn
при n
удовлетвор. з-ну больших чисел, если
выполн. соотношение: limn(D(Sn)/n2)=0,
Sn=x1+x2+…+xn.
При этих условиях справедлив з-н больших
чисел. Теорема
Чебышева:
с.в. x1,x2,…,xn
удовл. з-ну больших чисел, если эти случ.
велич. независимы и дисперсия каждой
случ. величины огранич. некоторой
константой L:
D(xi)<=L,
i=1,2,…,n.
Теорема
(нер-ва Чебышева):
с.в. X,
X>=0,
такая, что мат.ожид. сущ. EX<,
тогда для любого числа t>0
справедливо нер-во: p(x>t)<=EX/t.
Док-во теоремы
Маркова:
возьмем (**): p{|
-
|>}=[x=|
-
|2,
t=2]<=(E|
-
|2)/2=D(Sn)/2n20
(***), т.к. D(Sn)/n20.
E|
-
|2=E((1/n)i=1nxi-(1/n)
i=1nmi)2=E((1/n)i=1n(xi-mi))2=(1/n2)E(i=1n(xi-mi))2=(1/n2)D(Sn),
ч.т.д. Док-во
теоремы Чебышева:
D(Sn)=i=1nD(xi)<=
i=1nL=nL,
тогда в соотношении (***): D(Sn)<=nL,
p{|
-
|>}<=L/n0,
ч.т.д.
=(1/n)(m1+m2+…+mn)
– среднее знач. мат.ожид.;
-
случайное среднее,
-
неслучайное. Пос-ть с.в. {xn}
при n
удовлетвор. з-ну больших чисел, если
для любого достаточно малого числа
(>0)
выполняется соотношение:
limnp{|
-
|<=}=1(*)
– сходимость по вер-ти, |
-
|
- разность будет сколь угодно мала =>
E
=
.
Перепишем соотношение (*) иначе:
p{|
-
|<=}+p{|
-
|>}=1,
[|
-
|<=]-А,
[|
-
|<]-
(
A=).
p{|
-
|>}=1-p{|
-
|<=},
limnp{|
-
|>}0
(**). Условия для случ. величин x1,x2,…,xn,
для кот. выполняется з-н больших чисел.
Теорема
Маркова:
последов-ть с.в. x1,x2,…,xn
при n
удовлетвор. з-ну больших чисел, если
выполн. соотношение: limn(D(Sn)/n2)=0,
Sn=x1+x2+…+xn.
При этих условиях справедлив з-н больших
чисел. Теорема
Чебышева:
с.в. x1,x2,…,xn
удовл. з-ну больших чисел, если эти случ.
велич. независимы и дисперсия каждой
случ. величины огранич. некоторой
константой L:
D(xi)<=L,
i=1,2,…,n.
Теорема
(нер-ва Чебышева):
с.в. X,
X>=0,
такая, что мат.ожид. сущ. EX<,
тогда для любого числа t>0
справедливо нер-во: p(x>t)<=EX/t.
Док-во теоремы
Маркова:
возьмем (**): p{|
-
|>}=[x=|
-
|2,
t=2]<=(E|
-
|2)/2=D(Sn)/2n20
(***), т.к. D(Sn)/n20.
E|
-
|2=E((1/n)i=1nxi-(1/n)
i=1nmi)2=E((1/n)i=1n(xi-mi))2=(1/n2)E(i=1n(xi-mi))2=(1/n2)D(Sn),
ч.т.д. Док-во
теоремы Чебышева:
D(Sn)=i=1nD(xi)<=
i=1nL=nL,
тогда в соотношении (***): D(Sn)<=nL,
p{|
-
|>}<=L/n0,
ч.т.д.
45. Закон больших чисел для сумм независимых случайных величин.
З-н больших чисел: Sn=x1+x2+…+xn – сумма; =(1/n)Sn – среднее значение суммы; mi=EXi, i=1,2,…,n; =(1/n)(m1+m2+…+mn) – среднее знач. мат.ожид.; - случайное среднее, - неслучайное. Пос-ть с.в. {xn} при n удовлетвор. з-ну больших чисел, если для любого достаточно малого числа (>0) выполняется соотношение: limnp{| - |<=}=1(*) – сходимость по вер-ти, | - | - разность будет сколь угодно мала => E = . Перепишем соотношение (*) иначе: p{| - |<=}+p{| - |>}=1, [| - |<=]-А, [| - |<]- ( A=). p{| - |>}=1-p{| - |<=}, limnp{| - |>}0 (**). Условия для случ. величин x1,x2,…,xn, для кот. выполняется з-н больших чисел.
46. Центральная предельная теорема теории вероятности.
x1,x2,…,xn явл. послед-тью независ. одинаково распредел. с.в. (т.е. одна и та же ф-ция распределения). Fx1(x)=p{x1<x}, Fx1(x)=Fx2(x)=Fx3(x)=…=Fxn(x). EX1=m – мат.ожид. DX=E(x1-m)2=2 – дисперсия. Sn=x1+x2+…+xn: Yn=(1/(n))i=1n(xi-m). FYn(x) – вер-ть того, что Yn<x, FYn(x)=p{Yn<x}, xR. - стандартн. нормальн. с.в. E=0, D=1, F(x)=p{<x}=Ф(x)=(1/2)-xe dt. Теорема (ЦПТ): если n, тогда max по всем x = maxx|FYn(x)-F(x)|0, или limnp{Yn<x}=Ф(x), xR. n => p{Yn<x}Ф(x).
47. Метод наименьших квадратов
!!!(X,Y)-сл-й в-р, g(x)-нек-я ф-я от сигн-а Х,
E(Y-g(X))2 выб-т такую ф-ю g(x)б чтобы это было мин-м. Эта проц-ра опр-я ф-ии g(x) наз-ся методом наим-х кв-в. Ф-я g, на к-й дост-ся этот мин-м, наз-ся оценкой, пол-й по мет-у наим-х кв-в.
