9. Функция распределения случайной величины.
{,F,p}, X=X() – случ. величина, xR = (-, +), {:X()<x} со случ величиной X() мы связываем случайное событие, состоящее в том, что случайная величина X() строго <x. Обозначим F(x) вер-ть этого события: F(x)=p{:X()<x}, F(x)=p(X<x). Ф-цию от веществ. аргумента x назыв. ф-цией распределения случ. величины X.
10. Свойства функции распределения.
1. для всех xR: 0<=F(x)<=1. Док-во: по определ.: F(x)=p{:X()<x}; 0<=p{:X()<x}<=1 => 0<=F(x)<=1, ч.т.д.
2. для x1<x2: F(x1)<=F(x2), ф-ция F(x) – неубывающая. Док-во: F(x2)=p(X<x2)=p{(X<x1)(x1<=X<x2)} => p(X<x1)+p(x1<=X<x2)= F(x1)+p(x1<=X<x2)>=F(x1), ч.т.д.
3. x1<x2: p(x1<=X<x2)=F(x2)-F(x1), x1,x2R, x1>x2. Следствие: p(X<x)=1-p(X>=x), xR.
4. limx- F(x)=0; limx+F(x)=1.
5. Ф-ция F(x) непрерывно слева. Док-во: limxx0-F(x)=F(x0-)=F(x0); limxx0+F(x)=F(x0+); F(x0+)F(x0) – для ф-ции непрерыв. слева. Ф-ция F(x) в (.) x0 назыв. непрерывной, если предел слева совпадает с пределом справа: F(x0-o)=F(x0+o).
11. Случайные величины дискретного типа.
{,F,p}, X: X()R. Случ. величина X() назыв. дискретной (случ. величиной дескр. типа), если мн-во ее возможных значений не более чем счетно (т.е. ее значения можно занумировать): x1,x2,…,xn,… или {xn}1* - значения случ. величины, кот. мы можем занумировать. Ak={:X()=xk}, k=1,2,…, где Ak – мн-во элементарных событий, при кот. значение дискр. величины = xk. pk=p(Ak) – вер-ть того, что дискр. случ. величина примит значение xk. Для того, чтобы задать дискр. случ. величину достаточно задать табл.:
Х[значения/вер-ти]
x1 |
x2 |
… |
xn |
… |
p1 |
p2 |
... |
pn |
… |
pn=p{X=xn}; n=1pn=1. Если число столбцов конечно: Nn=1pn=1. Данная табл. назыв. з-ном распределения дискр. случ. величины.
Пример дискретной случайной величины: геометрическое распределение.
Для того чтобы задать дискретную случайную величину достаточно задать следующую таблицу:
-
x
….
….
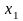
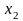
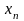
p
….
….
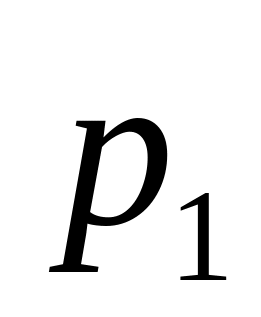
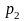
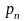
pn=p{X=xk}; i=1pn=1;
эта таблица-закон распределения дискретной случайной величины
Пример: x{-1,0,1}; p1=p{x=-1}=1/3; p2=p{x=0}=1/2; p3=p{x=1}=1/6.
x |
-1 |
0 |
1 |
p |
1/3 |
1/2 |
1/6 |
12. Математическое ожидание дискретной случайной величины. Свойства математического ожидания.
Мат. ожиданием дискретн. случ. величины X, обозначаемым как ЕX, называется следующая сумма ряда: EX=x1p1+x2p2+…+xnpn+…= n=1xnpn, при условии, что ряд сходится абсолютно: n=1|xn|pn<. Мат. ожидание (expectation) – ожидаемое среднее значение x. Мат. ожидание не явл. случайной величиной, это определенное число.
Св-ва:
1. если X=C=const, то EX=C (матожид совпадает с постоянной).
Док-во: X
C |
1 |
EX=k=1xkpk=C1=C, ч.т.д.
2. X – случ. величина дескр. типа, а=const, тогда: EX(aX)=aEX. Док-во: E(aX)=k=1(axk)pk=ak=1xkpk=aEX, ч.т.д.
3. пусть X и Y – случ. величины дискр. типа, тогда: E(X+Y)=EX+EY.
4(2+3). пусть X и Y – случ. величины дискр. типа, а а1 и а2 – любые константы, тогда: E(XY)=(EX)(EY).