4. Теорема сложения вероятностей.

{, F, p}, A,BF, p(A),p(B), AB=: p(A+B)=p(A)+p(B). Теорема (сложение в-тей): для любых А и В (A,BF): p(A+B)=p(A)+p(B)-p(AB). Док-во: AB=(A )(B )(AB); (A )(B )(AB)= => p(AB)=p(A )+p(B )+p(AB) (*); (A )(AB)=A (по 3 аксиоме) => p(A )+p(AB)=p(A) => p(A )=p(A)-p(AB); (B )(AB)=B (по 3 аксиоме) => p(B )+p(AB)=p(B) => p(B )=p(B)-p(AB). Подставим все в (*): p(A)-p(AB)+p(B)-p(AB)+p(AB)=p(A)+p(B)-p(AB), ч.т.д.

5. Условная вероятность.

Пусть имеются 2 события: A, B. Известно, что событие В произошло. Как определить в-ть события А при условии, что событие В уже произошло: p(A|B): p_n(A|B)=K_n(AB)/K_n(B)=(K_n(AB)/n)/(K_n(B)/n)=p_n(AB)/p_n(B).

6. Теорема умножения вероятностей. Независимые события.

Пусть есть:{ ,F,P}-вероятностное пространство. 1) -простр-во элементарн событий.2) F-алгебра событ. 3)Р-вер-ть событ. А,В F: Р(А),Р(В)0Р(AB)=Р(A|B)*Р(В)= Р(В|А)*Р(А).Если событие В не влияет на событие А, то вер-ть А при условии В равно вер-ти А: Р(A|B)=Р(А), Если соб А не влияет на соб В, то Р(В|А)= Р(В) Р(AB)=Р(А)*Р(В) (события А и В независимы между собой).

Независимые события. Независимыми событиями называют такие события А и В для которых вероятность появления одного события не изменяется при наступлении другого, т.е. P(A∩B) = Р(А|B) + Р(В) = Р(B|A) + Р(A) => P(A∩B) = P(A)*P(B).

Случайные события назыв. независимыми в совокупности, если для любого целого числа m=2,3,…,n, в-ть пересечения: p(A_iA_i2 … A_im)=p(A_i1)p(A_i2) …p(A_im){1,2,…,n}, если m=n, тогда в-ть: p(A₁A₂…A_n)=p(A₁) p(A₂)…p(A_n); i,j (ij): p(A_iA_j)=p(A_i)p(A_j). Теорема умножения в общем случае: {, F, p}, A₁,A₂,…,A_nF: p(A₁A₂…A_n)=p(A₁)p(A₂|A₁)p(A₃|A₁A₂)p(A₄|A₁A₂A₃)…p(A_n|A₁A₂A_n-1) для n>=2.

7. Формула полной вероятности. Теорема Байеса.

{, F, p}. Имеется набор событий: B₁,B₂,…,B_nF, кот. назыв. полной группой событий, если выполняются св-ва: 1. любые 2 события дают пусто на пересечении: B_iB_j=, ij; 2. объединение всех событий, есть достоверное событие: B₁B₂…B_n=. Теорема: предположим, что события B₁,B₂,…,B_n образуют полную группу и таковы, что p(B_i)0, i=1,2,…,n. Пусть имеется любое другое событие AF, тогда в-ть события А: p(A)=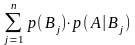 - ф-ла полной в-ти. Док-во: A=A=A(B₁B₂…B_n)=(AB₁)(AB₂)…(AB_n). Заметим, что можно использ. аксиому 3: (AB_i)(AB_j)= если ij => p(A)=p{(AB₁)(AB₂)…(AB_n)}= . 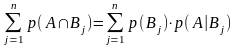По ф-ле p(A|B)=p(AB)/p(B) => p(AB)=p(B)p(A|B) => , ч.т.д. События B₁,B₂,…,B_n назыв. гипотезами.

Теорема Байеса: {,F,p}; B₁,B₂,…,B_n; AF; p(B_j)>0, j=1,2,…,n; p(A)>0, тогда ля каждого j=1,2,…,n справедлива ф-ла: p(B_j|A)=p(B_jA)/p(A)=(p(A|B_j)p(B_j))/ⁿ_i=1(p(B_i) p(A|B_i)).

8. Случайная величина. Определение. Пример.

Величина назыв. случайной, если ее значение зависит от случая. {,F,p}, {}, где  - элементарн. событие: X,Y,Z…или ,,… - случ. величины. X=X() – ф-ция от аргумента омега. Случайной величиной X будем называть правило, согласно кот. элементарному событию  сопоставл. в соответствие вещественное число X(), причем правило такое, что мн-во элементарн. событий {:X()<x}F для любого xF: X: X()R (определяет по какому правилу зависит X() от случая) {:X()<x}F; xR (для любого значения данной случ. величины сущ. или определена в-ть, с кот. случ. величина может принимать те или иные значения). 2 типа случ. величин: 1. дискретные: это величины, значение кот. можно занумировать, т.е. дискр. случ. величины приним. отдельно изолированные значения. 2. непрерывные: это величины, значение кот. заолняют сплошь некоторый интервал -> знач. непрерыв. случ. веkличины нельзя занумировать.