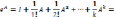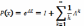- •1. Случайные события и действия над ними.
- •2. Алгебра событий.
- •3. Вероятность события. Свойства вероятности.
- •4. Теорема сложения вероятностей.
- •5. Условная вероятность.
- •6. Теорема умножения вероятностей. Независимые события.
- •7. Формула полной вероятности. Теорема Байеса.
- •8. Случайная величина. Определение. Пример.
- •9. Функция распределения случайной величины.
- •10. Свойства функции распределения.
- •11. Случайные величины дискретного типа.
- •12. Математическое ожидание дискретной случайной величины. Свойства математического ожидания.
- •13. Дисперсия дискретной случайной величины. Свойство дисперсии.
- •14. Производящая функция дискретной случайной величины.
- •15. Формулы для математического ожидания и дисперсии дискретной случайной величины через производящую функцию.
- •16. Схемы испытаний Бернулли.
- •17. Биномиальное распределение.
- •18. Математическое ожидание, дисперсия и производящая функция биномиальной случайной величины.
- •19. Мода биномиального распределения.
- •20. Распределение Пуассона.
- •21. Предельная теорема Пуассона.
- •22. Локальная предельная теорема Муавра-Лапласа.
- •23. Интегральная предельная теорема Муавра-Лапласа.
- •24. Дифференциальная и интегральная функции Гаусса.
- •25. Закон больших чисел в схеме Бернулли.
- •26. Непрерывные случайные величины. Свойство плотности распределении.
- •27. Равномерное распределение.
- •28. Нормальное распределение.
- •29. Показательное распределение.
- •31. Мода непрерывной случайной величины.
- •32. Медиана непрерывной случайной величины.
- •33. Математическое ожидание непрерывной случайной величины. Свойства математического ожидания.
- •39. Двумерные непрерывные случайные величины.
- •40. Числовые характеристики системы двух случайных величин.
- •41. Коэффициент ковариации и его свойства.
- •42. Коэффициент корреляции и его свойства.
- •43. Виды сходимости последовательности случайных величин.
- •44. Неравенство Чебышева.
- •45. Закон больших чисел для сумм независимых случайных величин.
- •46. Центральная предельная теорема теории вероятности.
- •47. Метод наименьших квадратов
- •48. Линейная среднеквадратическая регрессия
- •49. Генеральная совокупность. Случайная выборка. Вариационный ряд.
- •50. Эмпирическая функция распределения. Теорема Гливенко.
- •51. Выборочное среднее значение и выборочная дисперсия. Сходимость к теоретическим значениям.
- •52. Выборочный коэффициент ковариации.
- •53. Выборочный коэффициент корреляции.
- •54. Доверительные интервалы для неизвестного математического ожидания нормального распределения.
- •55. Критерий x2.
- •5 6. Понятие случайного процесса. Определение и примеры
- •57. Марковские процессы. Переходные вероятности
- •58. Теорема Колмогорова-Чепмена для переходных вероятностей
- •59. Дифференциальные уравнения Колмогорова для переходных вероятностей
- •60. Уравнения Колмогорова в стационарных режимах
5 6. Понятие случайного процесса. Определение и примеры
!!!
Случа́йный
проце́сс (случайная функция) в теории
вероятностей — семейство
случайных величин, индексированных некоторым параметром,
чаще всего играющим роль
времени или координаты.
Пусть дано вероятностное
пространство  .
Параметризованное семейство
.
Параметризованное семейство 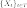 случайных
величин
случайных
величин
 ,
,
где T произвольное множество, называется случайной функцией.
 ,
где
,
где 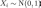 называется
стандартной гауссовской
(нормальной) случайной
последовательностью.
называется
стандартной гауссовской
(нормальной) случайной
последовательностью.Пусть
 ,
и Y —
случайная величина. Тогда
,
и Y —
случайная величина. Тогда
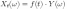
является случайным процессом.
Случайная функция – ф-я неслуч-го арг-та t, к-я при каждом фикс-м знач-и арг-та явл-ся сл-й вел-й. X(t), Y(t). Если U-сл-я вел-на, то X(t)=t2U-сл-я. Ее можно рассм-ть как совок-ть сл-х вел-н {X(t)}, зав-х от пар-ра t. Случайный процесс-сл-я ф-я арг-та t, к-й истолк-ся как время. Если арг-т сл-й ф-ии изм-ся дискр-но, то соотв-е ему знач-я сл-й ф-ии обр-т сл-ю посл-ть.
57. Марковские процессы. Переходные вероятности
!!! Ма́рковский проце́сс — случайный процесс, эволюция которого после любого заданного значения временно́го параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»; другая трактовка (Вентцель): «будущее» процесса зависит от «прошлого» лишь через «настоящее»)
Ц
 епь
Маркова-посл-ть исп-й, в каждом из к-х
появл-ся только одно из к несовместных
соб-й
епь
Маркова-посл-ть исп-й, в каждом из к-х
появл-ся только одно из к несовместных
соб-й  полной группы, причем усл-я вер-ть
полной группы, причем усл-я вер-ть 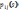 т.что в s-м
исп-ии наступит соб-е , при усл-ии, что
в S-1-м
исп-ии наступило соб-е
т.что в s-м
исп-ии наступит соб-е , при усл-ии, что
в S-1-м
исп-ии наступило соб-е 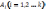 ,
не зав-т от рез-в предш-х исп-й.
,
не зав-т от рез-в предш-х исп-й.
Однор-я цепь Маркова – если усл-я вер-ть (перехода из сост-я i в j) не зав-т от номера исп-я.
Перех-я вер-ть pij-усл-я вер-ть т.что из сост-я i(в к-м сист-ма ок-сь в рез-те нек-го исп-я, безразл-но, какого номера) в итоге след-го исп-я сист-а перейдет в сост-е j.
Т
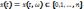 .
колмогорова. При нек-х усл-х каждому
конечномерному проц-у отвечает нек-й
сл-й пр-с, если он есть, то он единств-й.
.
колмогорова. При нек-х усл-х каждому
конечномерному проц-у отвечает нек-й
сл-й пр-с, если он есть, то он единств-й.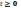
Сл-й
пр-с д-го вида обл-т марк-м спос-м, если
вып-ся сл-е св-во: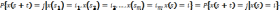 .
Если эта усл-я вер-ть не зав-т от s,
то марк-й пр-с однор-й, если
.
Если эта усл-я вер-ть не зав-т от s,
то марк-й пр-с однор-й, если 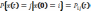
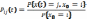
x(t),
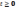 ,
,
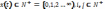
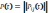
-дост-но прим-ть ф-лу полной вер-ти
x(t)-число
индивидов в д-й мом-т вр-ни, 
метод
закл-ся в сл-м: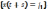
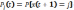 -вероятностное
сост-е,
-вероятностное
сост-е, 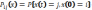 -перех-я
вер-ть
-перех-я
вер-ть
Теорема.
Пусть x(t)-однор-я
цепь Маркова. Фикс-м мом-ты вр-ни 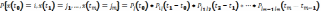
Т.о,
эта т-ма гов-т о следующем: однор-е марк-е
цепи опр-ся нач-м распр-м пр-в и нач-ми
мом-ми 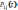 .Для
док-ва дост-но лишь восп-ся Марк-м св-м
.Для
док-ва дост-но лишь восп-ся Марк-м св-м
58. Теорема Колмогорова-Чепмена для переходных вероятностей
!!!
Справ-ва ф-ла 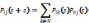
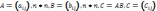
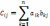
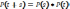 -урв-е
К-Ч – произв-е двух м-ц
-урв-е
К-Ч – произв-е двух м-ц
intinitisimating matrix – м-ца интенсивностей
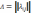
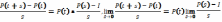
 если
этот пр-л сущ-т, то м-ца наз-ся интенс.
если
этот пр-л сущ-т, то м-ца наз-ся интенс.
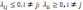
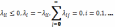
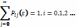

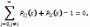
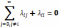
В м-це 𝜦 сумма эл-в в каждой строке =0, а все стоящие на гл-й диаг-ли «-»
59. Дифференциальные уравнения Колмогорова для переходных вероятностей
!!!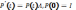
Док-во:
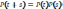
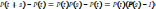
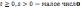
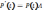
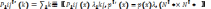 -кол-во
урв-й)
-кол-во
урв-й)
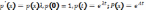 -м-я
экспонента
-м-я
экспонента