
- •Предмет, метод и задачи статистики:
- •Предмет статистики
- •Статистическая совокупность и статистический показатель Статистическая совокупность
- •Статистический показатель
- •Понятие и формы статистического наблюдения
- •Понятие и виды статистического наблюдения
- •Виды статистического наблюдения
- •Понятие и способы статистического наблюдения
- •Способы статистического наблюдения
- •Контроль статистического наблюдения
- •Понятие, виды, этапы, программа и план сводки Понятие, виды и этапы сводки
- •Программа и план сводки
- •8.Понятие и виды групповых данных
- •9.Проведение первичной и вторичной группировки
- •Вторичная группировка
- •10.Понятие и классификация статистических показателей
- •11.Абсолютные и относительные показатели
- •Относительные показатели
- •12.Функции статистических показателей
- •13.Статистический ряд распределения: понятие, виды, характеристики Статистические ряды распределения
- •14.Статистические графики
- •15.Понятие средней величины. Средняя арифметическая и её свойства
- •Средняя арифметическая и ее свойства
- •16.Понятие средней величины. Виды средних и их соотношение
- •17. Понятие средней величины. Структурные характеристики.
- •18.Показатели размера вариации
- •19. Показатели асимметрии и эксцесса распределения
- •20. Понятие и причины использования выборочного наблюдения
- •Виды и схемы отбора
- •21. Ошибка выборки
- •22. Определение объёма выборки. Распространение данных выборочного наблюдения на генеральную совокупность
- •Распространение данных выборочного наблюдения на генеральную совокупность
- •23. Понятие рядов динамики динамики. Показатели изменения уровней ряда динамики. Средние показатели динамики.
- •. Показатели динамики
- •Средние показатели динамики
- •24. Анализ основной тенденции в рядах динамики
- •25. Понятие рядов динамики. Измерение устойчивости в динамике
- •Измерение устойчивости в динамике
- •26. Понятие и виды индексов. Индивидуальные индексы
- •Индивидуальные индексы
- •27. Понятие и виды индексов. Агрегатные индексы
- •Агрегатные индексы
- •28. Понятие и виды индексов. Индексы средней величины
- •Индексы средней величины
- •29. Понятие статистической гипотезы
- •30. Теоретические кривые распределения
- •31. Проверка гипотез о характере распределения
- •32. Основные виды взаимосвязей между показателями. Показатели взаимосвязи качественных переменных
- •11.2. Показатели взаимосвязи качественных переменных
- •Показатели взаимосвязи количественных переменных
- •33. Основные виды взаимосвязей между показателями. Показатели взаимосвязи качественных переменных см 32 вопрос.
- •34. Определение параметров парной линейной регрессии
- •35. Оценка надёжности параметров парной линейной регрессии
16.Понятие средней величины. Виды средних и их соотношение
Средняя величина – обобщающая количественная характеристика однородной совокупности явлений по определенному признаку. Характеризует величину изучаемого признака, приходящуюся на единицу совокупности.
Средняя гармоническая
Рассчитывается, когда изучаемые показатели связаны между собой как x и1/x (показатели на единицу времени, сырья и т.д.).
Средняя
гармоническая простая:
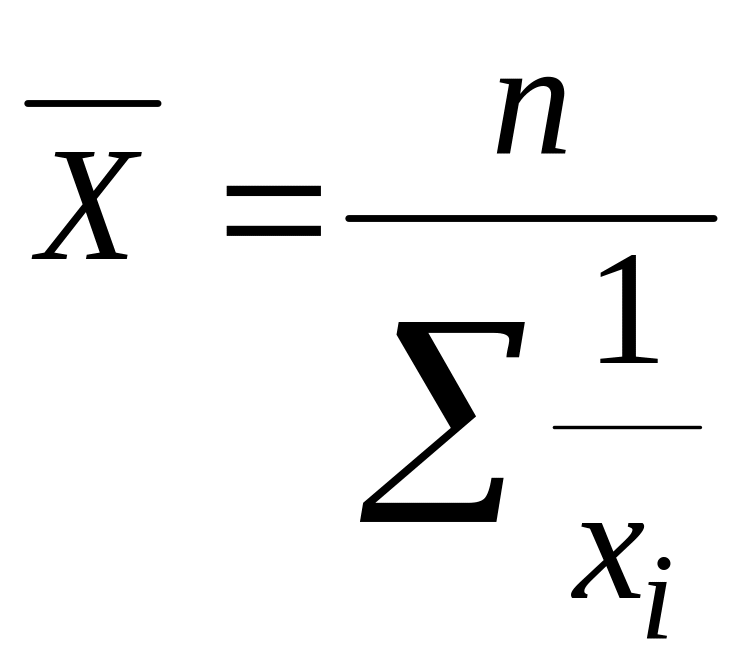 .
.
Пример 6.4. Требуется вычислить среднюю производительность труда бригады из 3-х человек, если первому рабочему требуется для изготовления одной детали 1/4 часа, второму - 1/3 часа, третьему - 1/2 часа.
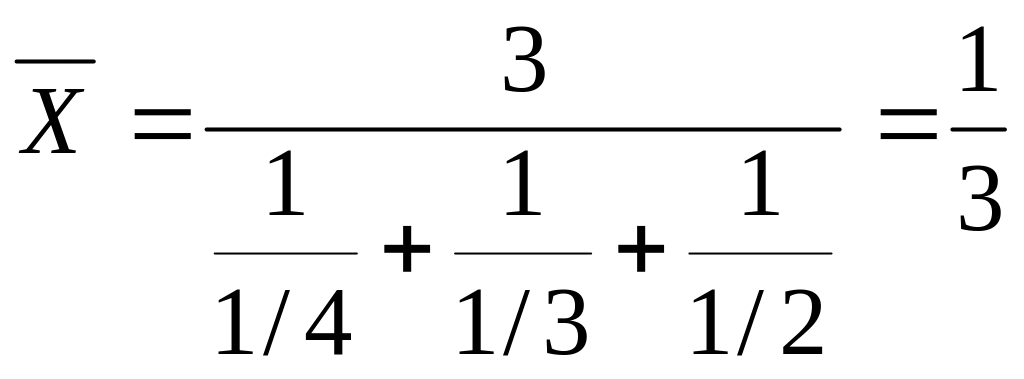 часа.
часа.
Средняя
гармоническая взвешенная:
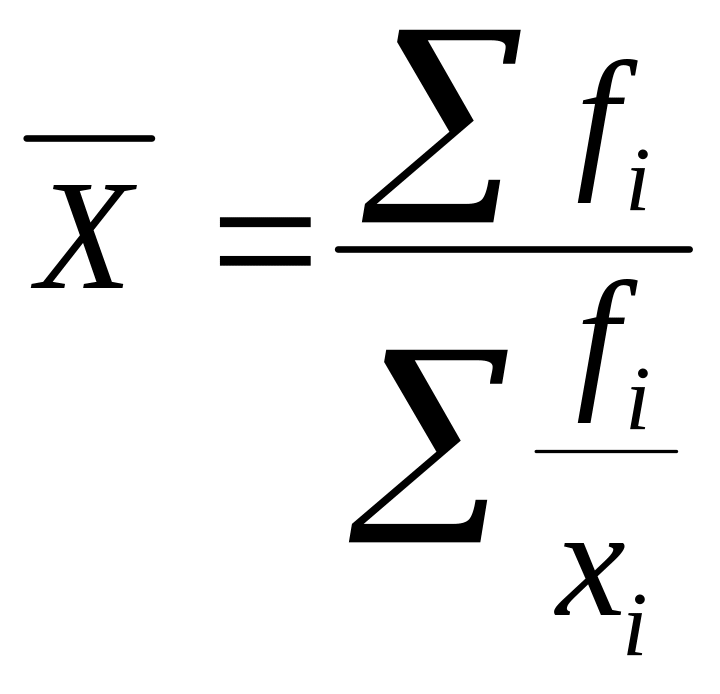 .
.
Средняя геометрическая
Применяется, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин.
![]() .
.
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
Пример 6.5. В результате инфляции за первый год цена товара возросла в 2 раза к предыдущему году, а за 2-й год еще в 3 раза к уровню предыдущего года. Т.е. за 2 года цена выросла в 6 раз. Какой средний темп роста цены за год?
Если
считать по средней арифметической, то
![]() раза,
тогда за два года выросла бы в 2,5 · 2,5 =
6,25 раза, а не в 6 раз.
раза,
тогда за два года выросла бы в 2,5 · 2,5 =
6,25 раза, а не в 6 раз.
Средняя геометрическая
дает правильный ответ:
![]() раза.
раза.
Средняя квадратическая
Применяется, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.
Средняя квадратическая простая:
 .
.
Пример 6.6. Имеется 3 участка земельной площади со сторонами квадрата: x1 = 100 м; x2 = 200 м; x3 = 300 м. Чему равна средняя площадь участков?
Общая площадь участков равна (100)2 + (200)2 + (300)2 = 140000 м2.
Если
считать по средней арифметической, то
![]() м2,
тогда общая площадь равна 3 · (200)2
= 120000 м2,
что неверно.
м2,
тогда общая площадь равна 3 · (200)2
= 120000 м2,
что неверно.
Средняя квадратическая дает правильный ответ:
![]() м2.
м2.
Средняя квадратическая взвешенная:
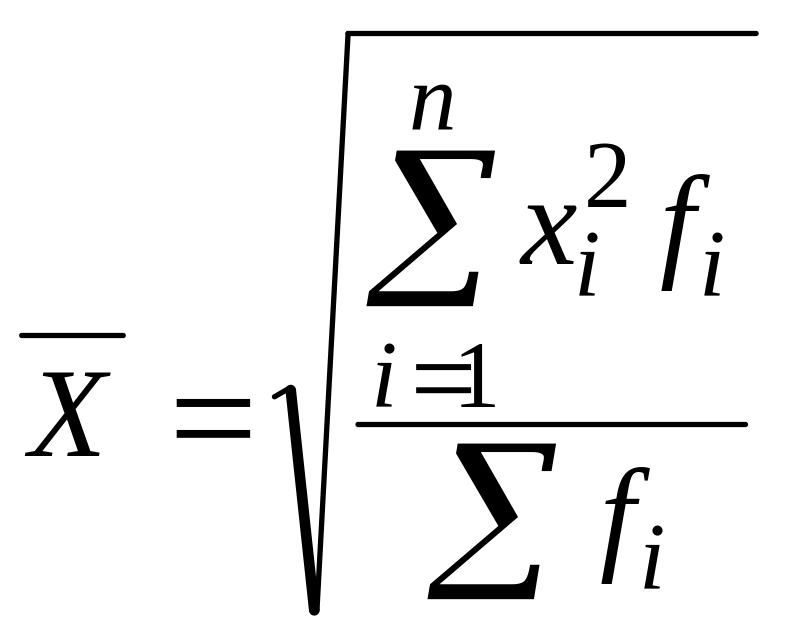 .
.
Средняя степенная
Обобщает все виды средних
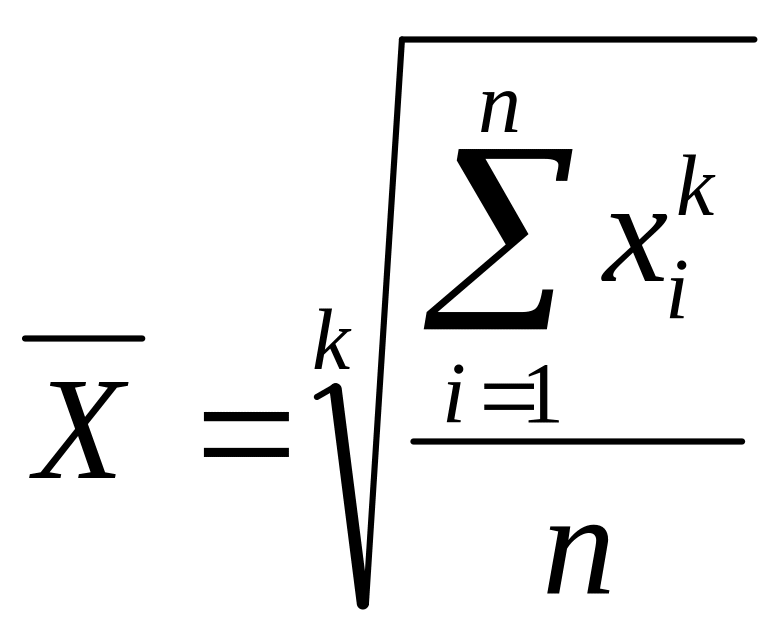 .
.
Если k = -1, то это средняя гармоническая,
k = 0 – средняя геометрическая (после преобразований),
k = 1 – средняя арифметическая,
k = 2 – средняя квадратическая,
k = 3 – средняя кубическая.
Имеется следующее соотношение между формами средних величин:
![]()
или
![]() .
.
Пользуясь этим правилом статистика может управлять средними.
Пример 6.7. Студент на экзамене получил за 1-й вопрос оценку 2, за 2-ой вопрос – 5.
![]() балла.
балла.
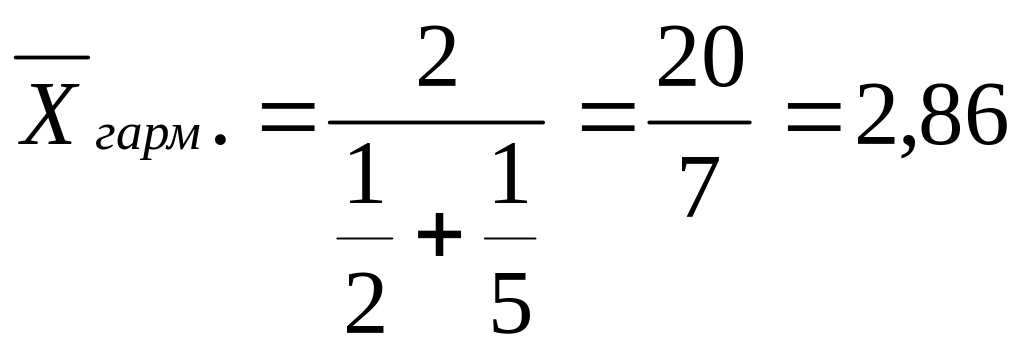 балла.
балла.
![]() балла.
балла.
Исходя из полученных средних можно как «завалить» студента, так и «вытянуть».
17. Понятие средней величины. Структурные характеристики.
Средняя величина – обобщающая количественная характеристика однородной совокупности явлений по определенному признаку. Характеризует величину изучаемого признака, приходящуюся на единицу совокупности.
Структурные характеристики
Если величина средней зависит от всех значений признака, встречаемых в данном распределении, то значение средней определяется структурой распределения, местом распределения.
Медиана – значение признака, приходящееся на середину ранжированной совокупности. Медиана делит совокупность на две равные части.
Пример. Вес 7 телят: 75, 80, 83, 87, 92, 97, 101 кг.
Медиана равна 87 кг (половина телят имеет вес меньше 87 кг, а половина – больше 87 кг).
Вес 8 телят: 75, 80, 83, 87, 92, 97, 101, 105 кг.
Медиана равна (87+92)/2=89,5 кг.
Медиана в интервальном ряду рассчитывается следующим образом:
Сначала
исчисляют порядковый номер медианы по
формуле
![]() и строят ряд накопленных частот Si=fi+Si-1
(S1=f1).
и строят ряд накопленных частот Si=fi+Si-1
(S1=f1).
Накопленной частоте, которая равна порядковому номеру медианы или первая его превышает, соответствует медианный интервал. Медиана равна:
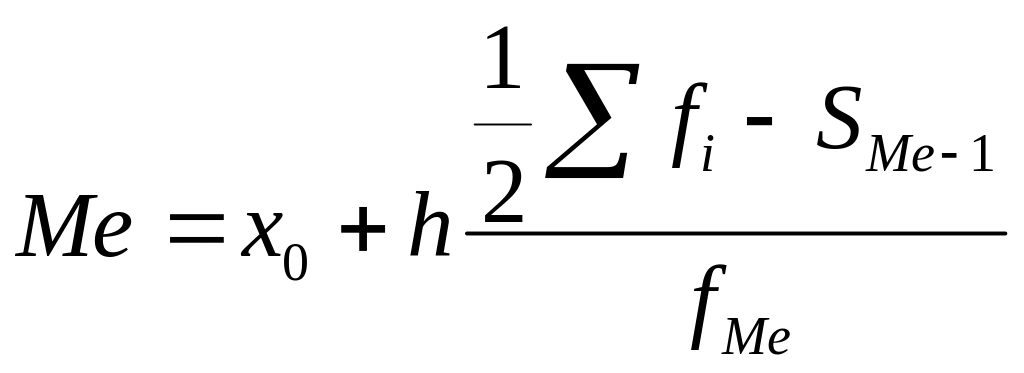 ,
,
где x0 – нижняя граница медианного интервала;
h – величина медианного интервала;
fi – частота i-го интервала;
Sме-1 – сумма накопленных частот в интервале, предшествующем медианному;
fMe – частота медианного интервала.
Пример Имеются данные о заработной плате рабочих:
Месячная з/п, $ |
Количество рабочих, fi |
Накопленные частоты, Si |
до 800 |
1 |
1 |
800 – 1000 |
3 |
4 |
1000 – 1200 |
4 |
8 |
1200 – 1400 |
1 |
9 |
1400 и более |
1 |
10 |
Итого |
10 |
- |
![]() ,
следовательно, медианный интервал
1000-1200.
,
следовательно, медианный интервал
1000-1200.
![]() $
(половина рабочих имеет заработную
плату ниже 1050$, а половина – выше 1050$).
$
(половина рабочих имеет заработную
плату ниже 1050$, а половина – выше 1050$).
Квартили – значения признака, делящие ранжированную совокупность на четыре равные по числу единиц части.
Номер квартильного интервала рассчитывается аналогично медианному в соотношении ¼ к совокупности. 1-й квартиль равен:
 ,
,
xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%),
h – величина интервала,
fQ1 – частота квартильного интервала,
SQ1-1 – сумма накопленных частот в интервале, предшествующего квартильному.
2-й квартиль:
Q2=Мe.
3-й квартиль:
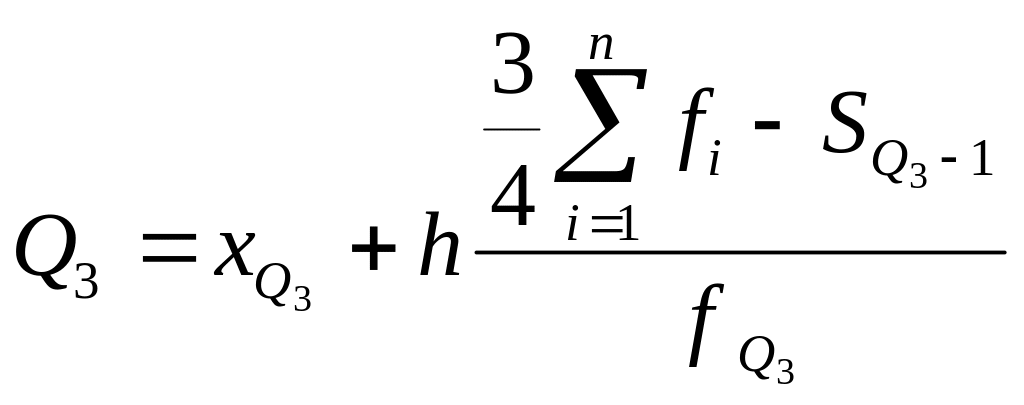 ,
,
обозначения аналогичны 1-му квартилю с изменением на номер интервала.
Пример. По данным примера 6.9.
![]() ,
следовательно, 1-й квартильный интервал
800-1000.
,
следовательно, 1-й квартильный интервал
800-1000.
![]() $
(25% рабочих получает заработную плату
ниже 900$).
$
(25% рабочих получает заработную плату
ниже 900$).
![]() ,
следовательно, 3-й квартильный интервал
1000-1200.
,
следовательно, 3-й квартильный интервал
1000-1200.
![]() $
(25% рабочих получает заработную плату
выше 1175$).
$
(25% рабочих получает заработную плату
выше 1175$).
Децили – значения признака, делящие ранжированную совокупность на десять равных по числу единиц частей.
Вычисляются они по той же схеме, что и медиана, и квартили. Обычно рассчитывают только первый и девятый децили:
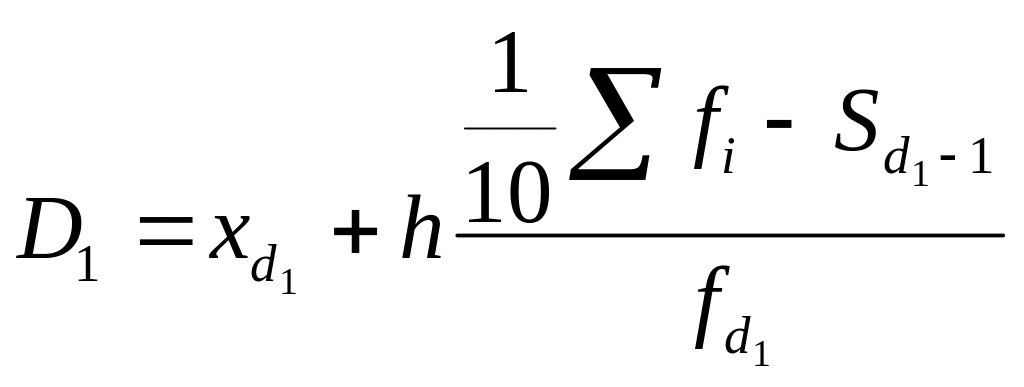 ,
,
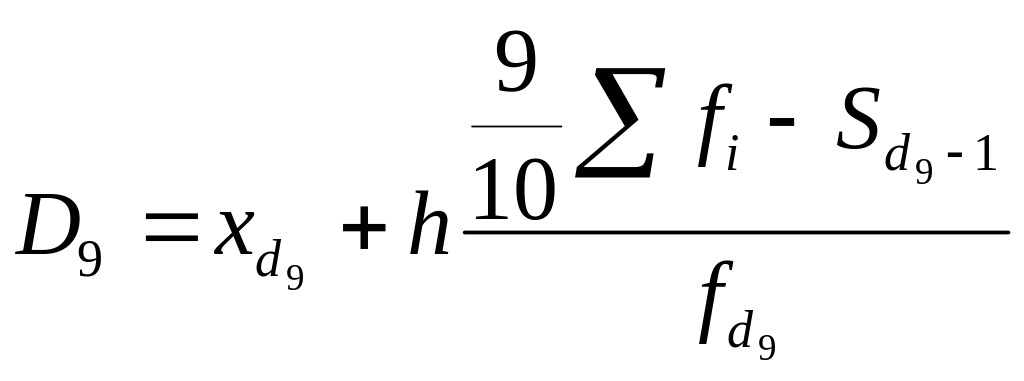 .
.
Пример. По данным примера 6.9.
![]() ,
следовательно, 1-й децильный интервал
до 800.
,
следовательно, 1-й децильный интервал
до 800.
![]() $
(10% рабочих получает заработную плату
ниже 800$).
$
(10% рабочих получает заработную плату
ниже 800$).
![]() ,
следовательно, 9-й децильный интервал
1200-1400.
,
следовательно, 9-й децильный интервал
1200-1400.
![]() $
(10% рабочих получает заработную плату
выше 1400$).
$
(10% рабочих получает заработную плату
выше 1400$).
Децильный
коэффициент
![]() .
Широко применяется при изучении
дифференциации доходов.
.
Широко применяется при изучении
дифференциации доходов.
Пример. По данным примера 6.11.
![]() (10% самых
высокооплачиваемых работников получают
зарплату в 1,75 раза больше 10% самых
низкооплачиваемых работников).
(10% самых
высокооплачиваемых работников получают
зарплату в 1,75 раза больше 10% самых
низкооплачиваемых работников).
Мода – значение признака, которое чаще других встречается в изучаемом ряду распределения.
Мода для дискретного ряда определяется как варианта, имеющая наибольшую частоту.
Для интервального ряда:
![]() ,
,
где x0 –нижняя граница модального интервала,
d- величина модального интервала,
fMo-1 - частота интервала, предшествующего модальному,
fMo - частота модального интервала,
fMo+1 - частота интервала, следующего за модальным.
Пример. По данным примера 6.9.
Модальный интервал с наибольшей частотой fi = 4 равен 1000-1200.
![]() $
(наибольшее число рабочих получает
зарплату 1050$).
$
(наибольшее число рабочих получает
зарплату 1050$).
