9.1.2. Метод последовательных приближений.

Рассмотрим задачу Коши для дифференциального уравнения первого порядка

с начальным условием . Решение этой задачи эквивалентно решению интегрального уравнения

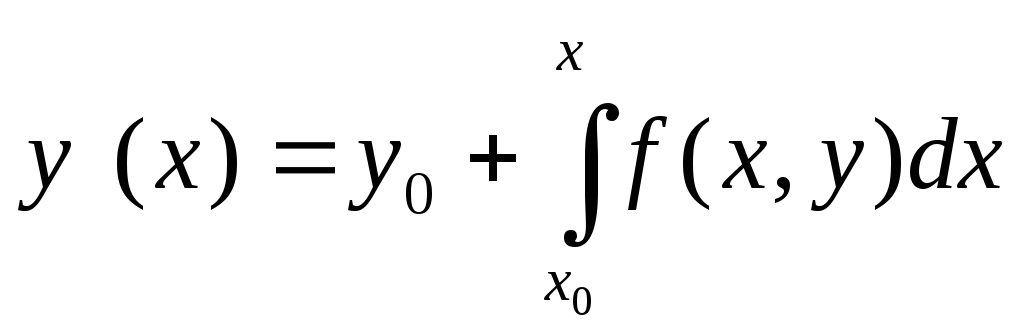
Метод последовательных приближений состоит в том, что решение получают как предел последовательности функций , которые находятся по рекуррентной формуле

.

Доказано, если правая часть в некотором замкнутом прямоугольнике удовлетворяет условию Липшица по y:

,

то независимо от выбора начальной функции последовательные приближения сходятся на некотором отрезке к решению задачи Коши.

Если f(x,y) непрерывна в прямоугольнике R, то оценка погрешности дается неравенством

,

где , а число h определяется из условия

.

В качестве начального приближения можно взять любую функцию, достаточно близкую к точному решению.

Пример 9.3. Найти три последовательных приближения решения уравнения

y^'=x²+y² с начальным условием y(0)=0.

Учитывая начальное условие, заменяем уравнение интегральным

В качестве начального приближения возьмем y₀(x)≡0

Первое приближение находим по формуле

Аналогично получим второе и третье приближения:

На практике количество приближений выбирают так, чтобы y_n и y_n-1 приближения совпадали в пределах допустимой точности. Для n=3 и

y₃ вычислено с точностью порядка 0.001.

9.1.3 Метод неопределенных коэффициентов.

Этот метод рекомендуют применять при решении линейных дифференциальных уравнений с переменными коэффициентами. Суть метода покажем на примере уравнения второго порядка

с начальными условиями . Предположим, что каждый из коэффициентов уравнения можно разложить в ряд по степеням x:

, , .

Решение данного уравнения будем искать в виде ряда

, (9.3)

где - коэффициенты, подлежащие определению.

Дифференцируем обе части равенства (9.3) два раза по x:

, .

Подставляя полученные ряды для в уравнение , получим:

. (9.4)

Произведя умножение рядов и приравняв коэффициенты при одинаковых степенях x в левой и в правой частях тождества (9.4), получим систему

(9.5)

где означает линейную функцию аргументов .

Каждое уравнение системы (9.5) содержит на одно неизвестное больше по сравнению с предыдущим уравнением. Коэффициенты определяются из начальных условий, а все остальные последовательно определяются из системы (9.5). Доказано, что если ряды , , сходятся при , то полученный степенной ряд сходится в той же области и является решением уравнения

.

Пример 9.4 Найти решение уравнения с начальными условиями в виде степенного ряда. Ограничиться 6 членами ряда.

Разложим коэффициенты уравнения в соответствующие степенные ряды.

p(x)=-x q(x)=-1

Будем искать решение уравнения в виде ряда

y=c₀+c₁x+c₂x²+ c₃x³+ c₄x⁴+…+c_nxⁿ+… тогда

y^'=c₁+2c₂x+3c₃x²+4c₄x³+…+n c_nx^n-1+…

-y^'x=-c₁x-2c₂x²-3c₃x³-4c₄x⁴-…- n c_nxⁿ+…

y^''=2c₂+6c₃x+12c₄x²+20c₅x³+…+n(n-1) c_nx^n-2+…

Подставив полученные ряды в уравнение примера, и приравняв коэффициенты при одинаковых степенях, получим систему для определения c_i .

c₀=0, c₁=1 возьмем из начальных условий.

x⁰ c₀ + 2 c₂ = 0,

x¹ 6 c₃ = 0,

x² – c₂ + 12 c₄ = ,

x³ – 2 c₃ + 20 c₅ = 0,

x⁴ – 3 c₄ + 30 c₆ = ,

x⁵ – 4 c₅ + 42 c₇ = 0,

x⁶ – 5 c₆ + 56 c₈ = .

Решая последовательно систему, получим, что нечетные коэффициенты нули, а

Приближенное решение задачи получаем в виде