4.4. Распространение метода итераций на системы из n уравнений с n неизвестными

Пусть дана система нелинейных уравнений специального вида:

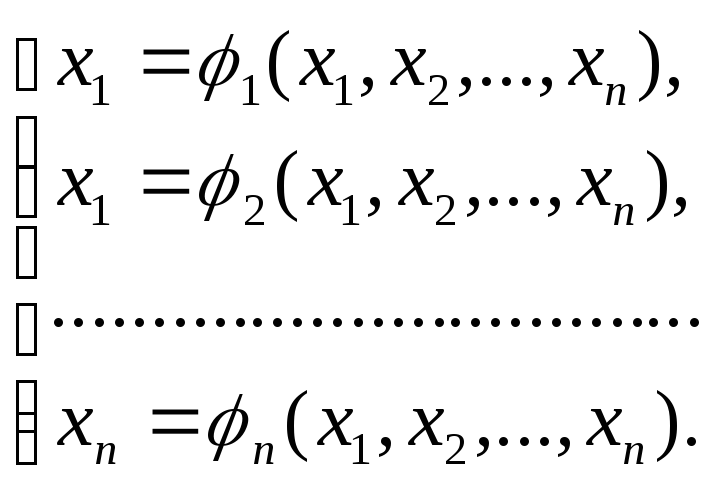
где функции действительны и определены и непрерывны в некоторой окрестности изолированного решения этой системы, или в более компактной записи:

,

где , а .

Для нахождения вектора-корня иногда можно использовать метод итерации

.

Если система уравнений задана в общем виде ,

где - вектор-функция, определенная и непрерывная в окрестности изолированного вектора-корня , то ее записывают в эквивалентном виде

, (4.3)

где - итерирующая вектор-функция, которую ищут в виде

.

Матрица  выбирается так (см. выше). Предполагается, что матрица неособенная.

Подставив в (4.3), получим итерационную формулу

.

Глава 5. Интерполяция

Вычисление значений функции y=f(x) – задача, с которой постоянно приходится сталкиваться на практике. В силу различных причин вычисление f(x)часто бывает затруднительно, например функция задана таблично, а вычисление необходимо проводить в точках не совпадающих с табличными. Вычисление f(x) может быть громоздким, требовать много операций. В таких условиях целесообразно заменить f(x) некоторой близкой к ней функцией g(x), которая вычисляется быстро и надежно, а погрешность приближения f(x)-g(x) достаточно мала. Требование совпадения функции g(x) с функцией f(x) в некоторых фиксированных точках приводит к задаче интерполяции.

5.1. Постановка задачи интерполирования

Пусть функция задана на отрезке в точках , i=0,1,2..n, называются узлами интерполяции.

Рис 5.1. Постановка задачи интерполирования

Требуется провести интерполирующую функцию определенного класса, проходящую через точки: , в узлах интерполяции i=1,2..n.

Пусть F(x)- это многочлен степени не выше n. Обозначим F(x) через P_n(x), тогда

В такой постановке задача имеет единственное решение. Полученную формулу y= P_n(x) используют для вычисления приближенного значения функции f(x) для значений аргумента x, отличных от узлов интерполяции. Эта операция называется интерполирование.

Если , то интерполирование будет в узком смысле, а если то интерполирование в широком смысле (экстраполирование).

5.2. Конечные разности

Пусть дана функция и фиксированная величина приращения аргумента . Конечной разностью первого порядка функции y называется выражение. Конечной разностью второго порядка называется: . Kонечной разностью n-го порядка называется . Конечные разности обладают следующими свойствами :

1. ;

2. ;

3. .

Для малых h можно приближенно заменять производные через конечные разности: , ().

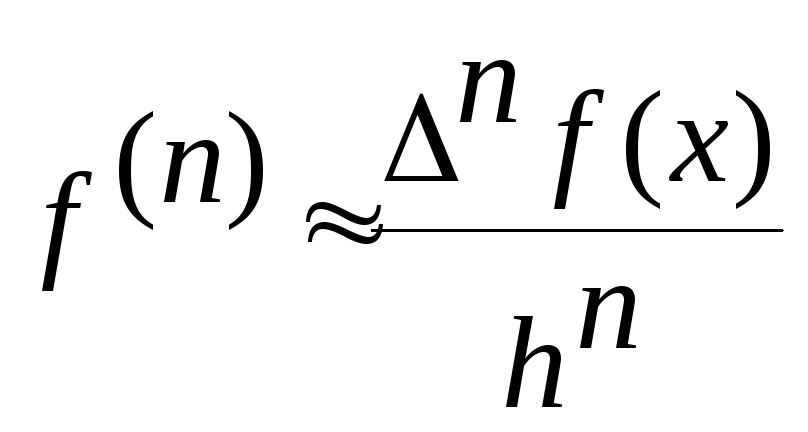Часто приходится рассматривать функции у=f(x), заданные табличными значениями y_i=f(x_i), для системы равноотстоящих точек x_i (i=0,1,2,…), где

. Конечные разности последовательности y_i определяются соотношениями

Пример 5.1 Построить конечные разности для функции с шагом .

Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной (таблица 5.1) или диагональной (таблица 5.2)

Таблица 5.1.

Горизонтальная таблица разностей

….	…	…	…	…	…

Таблица 5.2.

Диагональная таблица конечных разностей