Глава 9. Приближенное решение обыкновенных дифференциальных уравнений

Задача Коши для дифференциального уравнения n-го порядка:

(9.1)

заключается в отыскании функции , удовлетворяющей этому уравнению с начальными условиями:

,

где - заданные числа.

Задача Коши для системы дифференциальных уравнений

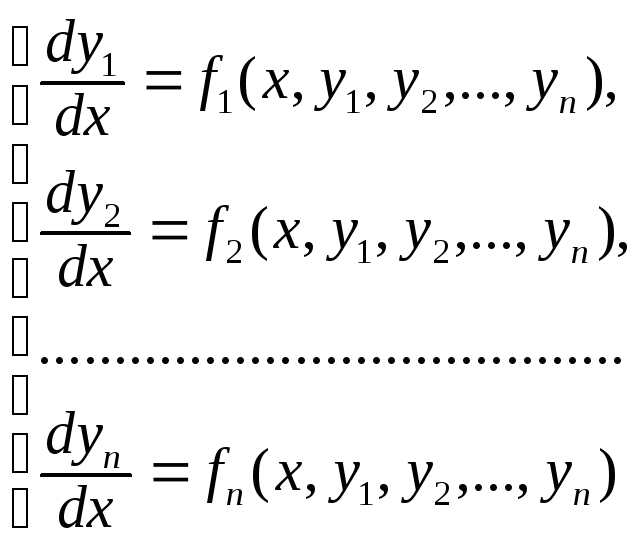(9.2)

заключается в отыскании функций , удовлетворяющих этой системе и начальным условиям

.

Систему, содержащую производные высших порядков и разрешенную относительно старших производных искомых функций, путем введения новых неизвестных функций можно привести в виду (9.2). В частности, дифференциальное уравнение n-го порядка

приводится к виду (9.1) с помощью замены переменных

,

что дает следующую систему

Если удается найти общее решение системы или уравнения, то задача Коши сводится к отысканию значений произвольных постоянных. Но найти общее решение задачи Коши удается в редких случаях, чаще приходится решать задачу приближенно.

Приближенные методы в зависимости от формы, в которой они представляют решение, можно разделить на две группы.

1. Аналитические методы, дающие приближенное решение дифференциального уравнения в виде аналитического выражения.

2. Численные методы, дающие приближенное решение в виде таблицы.

В дальнейшем будем считать, что для рассматриваемых уравнений выполнены условия существования и единственности решения.

9.1. Аналитические методы

9.1.1. Метод последовательного дифференцирования

Рассмотрим уравнение

(9.1)

с начальными условиями . Предположим, что искомое частное решение может быть разложено в ряд Тейлора по степеням разности :

Начальные условия непосредственно дают нам значения при . Значение найдем из уравнения (9.1), подставляя и используя начальные условия:

.

Значения последовательно определяются дифференцированием уравнения (9.1) и подстановкой , при .

Доказано, что если правая часть уравнения (9.1) в окрестности точки есть аналитическая функция своих аргументов, то при значениях x, достаточно близких к , существует единственное решение задачи Коши, которое разлагается в ряд Тейлора. Тогда частичная сумма этого ряда будет приближенным решением поставленной задачи.

Аналогично применяется метод последовательного дифференцирования и для решения систем дифференциальных уравнений.

Пример 9.1 Найти первые семь членов разложения в степенной ряд решения уравнения y^''+0.1(y')²+(1+0.1x)y = 0 с начальными условиями y(0)=1, y^'(0)=2

Решение уравнения ищем в виде ряда

Непосредственно из начальных условий имеем y(0)=1, y^'(0)=2

Разрешим уравнение относительно y^'';

y^''=-0.1(y^')²-(1+0.1x)

используя начальные условия, получим

y^''(0)=-0.1·4-1·1=-1.4

Дифференцируем по x обе части уравнения последовательно получим:

y^'''=0.2 y^'· y^''-0.1(xy^'+ y)- y^' y^'''(0)=-1.54

y⁽⁴⁾=-0.2(y^' y^'''+( y^'')²)-0.1(xy^''+2 y^')- y^'' y⁽⁴⁾(0)=1.224

y⁽⁵⁾= -0.2(y^'· y⁽⁴⁾+3 y^'' y^''') -0.1(xy^'''+3 y^'')- y^''' y⁽⁵⁾(0)=0.1768

y⁽⁶⁾(0)= -0.2(y^'· y⁽⁵⁾+4 y^'' y⁽⁴⁾+3(y^''')²)-0.1(x y⁽⁴⁾+4 y^''')- y⁽⁴⁾ y⁽⁶⁾(0) =-0.7308

Искомое решение приближенно запишется в виде:

y(x)≈1+2x-0.7x²-0.2567x³+0.051x⁴+0.00147x⁵-0.00101x⁶

Пример 9.2. Найти первые четыре члена разложения в степенной ряд решения y=y(x) z=z(x) системы с начальными условиями y(0)=1 z(0)=0

Функции y(x) и z(x) ищем в виде степенных рядов

при х=0 из уравнений системы следует, что y(0)'=1, z(0)'=0

Дифференцируем по х уравнения системы.

Находим y''(0)=1, z''(0)=1

Продифференцируем по х уравнения системы еще раз.

y''' (0)=0, z'''(0)=3

Подставляя найденные значения производных в ряды, получим:

y(x)≈1+x-0.5x², z(x)≈ 0.5x²-0.5x³