Глава 8. Численное интегрирование

Если функция непрерывна на отрезке и известна ее первообразная , то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона-Лейбница:

,

где . Однако, во многих случаях первообразная функция не может быть найдена с помощью элементарных средств.

Данную функцию на рассмотренном отрезке заменяют интерполирующей или аппроксимирующей функцией простого вида (например, полином), а затем приближенно полагают

.

Функция должна быть такова, чтобы вычислялся непосредственно. Если функция задана аналитически, то ставится вопрос об оценке погрешности этой формулы.

8.1. Квадратурные формулы Ньютона-Котеса

Рассмотрим применение в качестве интерполяционного полинома Лагранжа.

, (8.1)

где - ошибка квадратурной формулы (8.1) или остаточный член

Выбрав шаг ,разобьем отрезок с помощью равноотстоящих точек , , на n равных частей, и пусть . Заменяя функцию соответствующим интерполирующим полиномом Лагранжа

,

получим приближенную квадратурную формулу:

, (8.2)

- некоторые постоянные коэффициенты. Найдём явные выражения для коэффициентов формулы (8.2).

Коэффициенты полинома Лагранжа имеют вид:

,

где , причем .

Введем обозначения: и тогда

,

.

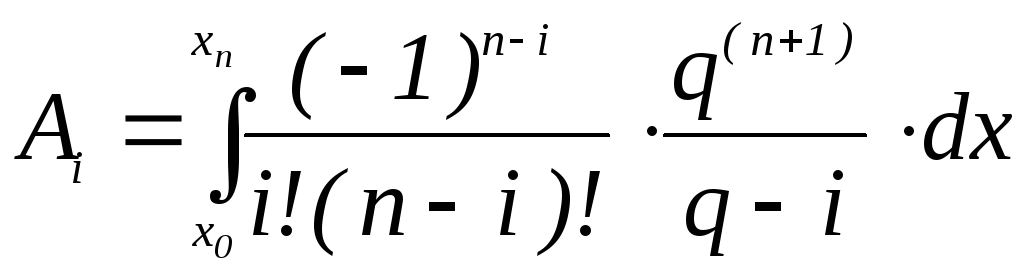Сделав замену переменных в определенном интеграле , будем иметь: .

Учитывая, что , обычно полагают , где это постоянные, называемые коэффициентами Котеса.

Квадратурная формула (8.2) принимает вид:

(8.3)

Формулы называются квадратурными формулами Ньютона-Котеса

Справедливы соотношения: 1. ; 2. .

8.1. Формула трапеций и ее остаточный член

При n=1 получим

, отсюда:

(8.4)

Если подынтегральная функция дважды дифференцируема, то остаточный член квадратурной формулы (8.4) равен:

, где

8.2. Общая формула трапеций и ее остаточный член

Рис 8.1. Общая формула трапеций

Для вычисления интеграла разделим промежуток интегрирования [a,b] на n равных частей и к каждому из них применим формулу трапеций (8.4).

Положим и обозначим через значения подынтегральной функции в точках x_i тогда: , или

. (8.5)

Геометрически формула (8.5) получается в результате замены графика подынтегральной функции ломаной линией.

Oстаточный член общей формулы трапеций (8.5) равен:

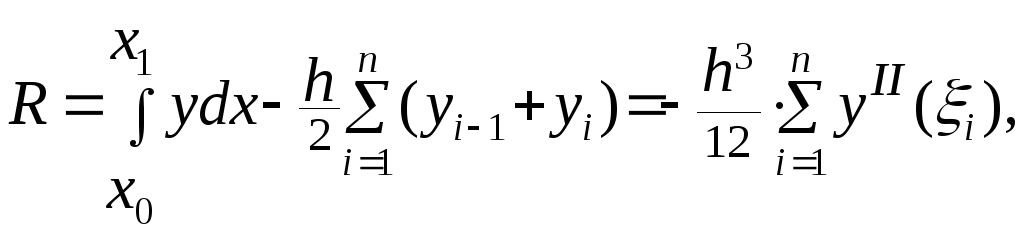где . (8.6)

Рассмотрим среднее арифметическое значение второй производной на отрезке [a,b] по всем промежуткам

(8.7)

Очевидно,  заключается между наименьшим m₂ и наибольшим M₂ значениями второй производной на отрезке [a,b], т.е. .

В силу непрерывности на отрезке [a,b], она принимает все значения от m₂ до M₂. Значит, существует точка ξ, такая что μ=f''(ξ). Из формул (8.6) и (8.7) получим:

(8.8)

где

Пример 8.1. Выполнено в Mathcad

Вычислить интеграл

по методу трапеций с тремя десятичными знаками.

Сначала для сравнения покажем результат, вычисленный в Mathcad стандартным способом с тремя верными цифрами после запятой.

В Mathcad числа могут быть вычислены с 17 десятичными знаками, поэтому не будем учитывать погрешности вычислений и тогда погрешность метода ε=0,0005. Для достижения заданной точности решим неравенство

находится по формуле

где R- остаточный член формулы трапеций, который находится по формуле (8.8)

Пусть M-максимальное по модулю значение f2(x) на [a,b] тогда

так как

Подставляем в формулу h и решаем неравенство относительно n:

Для всех натуральных значений "n" больших , чем полученный корень, остаточный член формулы трапеций будет меньше заданной точности 

Hайдем вторую производную f(x) и ее максимум на [a,b]

Найдем значение n, при котором остаточный член будет меньше заданной точности

Положим

Рис. 8.2. Решение примера 8.1 в Mathcad