
- •Введение
- •Глава 1. Погрешность результата численного решения задачи
- •1.1. Источники и классификация погрешностей
- •1.2. Абсолютная и относительная погрешности. Формы записи данных.
- •1.3. Вычислительная погрешность
- •Глава 2. Решение нелинейных уравнений
- •2.1. Отделение корней уравнения
- •2.1.1. Аналитический метод отделения корней
- •2.1.2. Графический метод отделения корней
- •2.2. Уточнение приближенных корней
- •2.2.1. Метод половинного деления
- •2.2.2 Метод хорд
- •2.2.3. Метод Ньютона – метод касательных
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Глава 3. Решения систем линейных алгебраических уравнений
- •3.1. Метод итераций
- •3.1.1. Оценка погрешности приближений процесса итераций
- •3.1.2. Приведение линейной системы к виду, удобному для итерации:
- •3.2. Метод Зейделя
- •3.3. Метод релаксаций
- •Глава 4. Решение систем нелинейных уравнений
- •4.1. Метод Ньютона для систем нелинейных уравнений
- •4.2. Распространение метода Ньютона на системы из n уравнений с n неизвестными
- •4.3. Метод итераций для систем нелинейных уравнений
- •4.4. Распространение метода итераций на системы из n уравнений с n неизвестными
- •Глава 5. Интерполяция
- •5.1. Постановка задачи интерполирования
- •5.2. Конечные разности
- •5.3. Интерполяционная формула Ньютона №1
- •5.4. Интерполяционная формула Ньютона №2
- •5.5. Интерполяционный многочлен Лагранжа
- •5.5.1. Вычисление лагранжевых коэффициентов
- •5.5.2. Схема Эйткина
- •5.5.3. Остаточный член формулы Лагранжа
- •5.6. Обратное интерполирование
- •5.6.1 Итерационные методы для обратного интерполирования
- •Глава 6. Аппроксимация функций с помощью сплайнов
- •6.1. Кубические сплайны
- •Глава 7. Методы обработки экспериментальных данных
- •7.1 Построение эмпирической формулы.
- •7.2. Метод выбранных точек (метод натянутой нити)
- •7.3 Метод средних
- •7.4. Метод наименьших квадратов
- •7.5. Метод выравнивания
- •7.6. Метод наименьших квадратов для полиномов
- •Глава 8. Численное интегрирование
- •8.1. Квадратурные формулы Ньютона-Котеса
- •8.1. Формула трапеций и ее остаточный член
- •8.2. Общая формула трапеций и ее остаточный член
- •8 .3 Формула Симпсона и ее остаточный член
- •8.4. Общая формула Симпсона и ее остаточный член
- •8.5. Формулы Ньютона-Котеса высших порядков
- •8.6. Квадратурная формула Чебышева
- •8.7. Квадратурная формула Гаусса
- •Глава 9. Приближенное решение обыкновенных дифференциальных уравнений
- •9.1. Аналитические методы
- •9.1.1. Метод последовательного дифференцирования
- •9.1.2. Метод последовательных приближений.
- •9.1.3 Метод неопределенных коэффициентов.
- •9.2. Численные методы
- •9.2.1. Метод Эйлера
- •9.2.2. Модифицированные методы Эйлера Первый улучшенный метод Эйлера
- •Второй улучшенный метод Эйлера
- •Третий улучшенный метод Эйлера
- •9.2.3. Метод Рунге-Кутта для уравнений первого порядка
- •Список литературы
8 .3 Формула Симпсона и ее остаточный член
Рис 8.2. Формула Симпсона
Найдем коэффициенты -Котеса для n=1
![]() .
.
![]()
![]()
Подставим в формулу (8.3)
 .
.
Если подынтегральная
функция
![]() четырежды
дифференцируема, то остаточный член
квадратурной формулы
Симпсона
равен:
четырежды
дифференцируема, то остаточный член
квадратурной формулы
Симпсона
равен:
![]()
8.4. Общая формула Симпсона и ее остаточный член
Пусть
n=2m
есть четное число и
![]() - значения функции
- значения функции
![]() для равноотстоящих точек
для равноотстоящих точек
![]() с шагом
с шагом
![]() .
Применяя формулу Симпсона к каждому
удвоенному промежутку
.
Применяя формулу Симпсона к каждому
удвоенному промежутку
![]() длины 2h,
будем иметь
длины 2h,
будем иметь
 .
.
Следовательно,
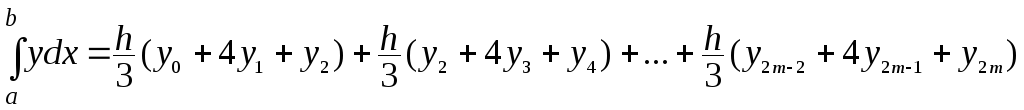 .
.
Отсюда получаем общую формулу Симпсона:
 .
.
Введя обозначения
 ,
формулу можно записать в более простом
виде:
,
формулу можно записать в более простом
виде:
![]() .
.
Если функция
непрерывно дифференцируема до четвертого
порядка, то ошибка формулы Симпсона на
каждом удвоенном промежутке
![]() дается формулой:
дается формулой:
![]() ,
где
,
где
![]() .
.
Суммируя все эти ошибки, получим остаточный член общей формулы Симпсона в виде:
 .
.
![]() непрерывна на
отрезке [a,b],
поэтому найдется точка
непрерывна на
отрезке [a,b],
поэтому найдется точка
![]() такая, что
такая, что
![]() .
.
Следовательно
![]() , (8.9)
, (8.9)
где
![]() .
.
Если задана
предельная допустимая погрешность
![]() ,
то, обозначив
,
то, обозначив
![]() ,
будем иметь для определения шага h
неравенство:
,
будем иметь для определения шага h
неравенство:
![]() ,
отсюда
,
отсюда
![]() ,
т.е. h
имеет порядок
,
т.е. h
имеет порядок
![]() .
Говорят, что степень точности метода
Симпсона равна четырем
.
Говорят, что степень точности метода
Симпсона равна четырем
Во многих случаях оценка погрешности квадратурной формулы весьма затруднительна. Тогда обычно применяют двойной пересчет с шагами h и 2h и считают, что совпадающие десятичные знаки принадлежат точному значению интеграла.
Предполагая, что
на отрезке [a,b]
производная
![]() меняется медленно, в силу формулы (8.9),
получаем приближенное выражение для
искомой ошибки
меняется медленно, в силу формулы (8.9),
получаем приближенное выражение для
искомой ошибки
![]() ,
где коэффициент M
будем считать постоянным на промежутке
интегрирования. Пусть
,
где коэффициент M
будем считать постоянным на промежутке
интегрирования. Пусть
![]() и
и
![]() - приближенные значения интеграла
- приближенные значения интеграла
 ,
полученные по формуле Симпсона
соответственно с шагом h
и H=2h.
Имеем:
,
полученные по формуле Симпсона
соответственно с шагом h
и H=2h.
Имеем:
![]() и
и
![]() .
Отсюда
.
Отсюда
![]() .
.
За приближенное значение интеграла целесообразно принять исправленное значение
![]() .
.
Пример 8.2 Вычислить в Mathcad интеграл методом Симпсона для n=8. Оценить остаточный член.


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вычисляем для формулы Симпсона при n=4



![]()
Сделаем двойной пересчет при n=8
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Остаточный член приблизительно равен
![]()
![]()

Это точный результат
Рис. 8.3. Решение примера 8.2 в Mathcad
8.5. Формулы Ньютона-Котеса высших порядков
Производя
соответствующие вычисления при n=3,
получим из формулы (8.3) и из выражения
![]() значения
значения
![]()
![]() и квадратурную формулу Ньютона:
и квадратурную формулу Ньютона:
 (правило
(правило
![]() ).
).
Остаточный
член формулы равен
![]() ,
где
,
где
![]() ,
т.е. при одинаковом шаге формула Ньютона,
вообще говоря, менее точна, чем формула
Симпсона.
,
т.е. при одинаковом шаге формула Ньютона,
вообще говоря, менее точна, чем формула
Симпсона.
8.6. Квадратурная формула Чебышева
Рассмотрим квадратурную формулу
![]() ,
(8.10)
,
(8.10)
где
![]() - постоянные коэффициенты. Чебышев
предположил выбрать абсциссы
- постоянные коэффициенты. Чебышев
предположил выбрать абсциссы
![]() таким образом, чтобы:
таким образом, чтобы:
-
коэффициенты
 были равны между собой;
были равны между собой; -
квадратурная формула (8.10) являлась точной для всех полиномов до степени n включительно.
Покажем, как могут
быть найдены в этом случае величины
![]() и
и
![]() .
Полагаем
.
Полагаем
![]() .
Учитывая, что при
.
Учитывая, что при
![]() ,
будем иметь
,
будем иметь
![]() ,
получаем
,
получаем
![]() .
Следовательно, квадратурная формула
Чебышева имеет вид:
.
Следовательно, квадратурная формула
Чебышева имеет вид:
![]() .
(8.11)
.
(8.11)
Для определения
абсцисс
![]() заметим, что формула (8.11) согласно условию
2 должна быть точной для функции вида
заметим, что формула (8.11) согласно условию
2 должна быть точной для функции вида
![]() .
Подставляя эти функции в формулу (8.11),
получим систему уравнений:
.
Подставляя эти функции в формулу (8.11),
получим систему уравнений:
 ,
(8.12)
,
(8.12)
из которой могут
быть определены неизвестные
![]() .
Заметим, что система (8.12) при n=8
и n10
не имеет действительных решений.
.
Заметим, что система (8.12) при n=8
и n10
не имеет действительных решений.
Выведем формулу Чебышева с тремя ординатами (n=3).
Для определения
абсцисс
![]() имеем систему уравнений:
имеем систему уравнений:
 (8.13)
(8.13)
Рассмотрим
симметрические функции корней:

Из системы (8.13)
имеем:

Отсюда заключаем
по теореме Виета, что
![]() есть корни вспомогательного уравнения
есть корни вспомогательного уравнения
![]() или
или
![]() .
Следовательно, можно принять:
.
Следовательно, можно принять:
![]() .
.
Таким образом,
соответствующая формула Чебышева имеет
вид
![]() .
.
Чтобы применить
квадратурную формулу Чебышева к интегралу
вида
![]() ,
следует преобразовать его с помощью
подстановки:
,
следует преобразовать его с помощью
подстановки:
![]() ,
переводящей отрезок
,
переводящей отрезок
![]() в отрезок
в отрезок
![]() .
Применяя к преобразованному интегралу
формулу Чебышева, будем иметь
.
Применяя к преобразованному интегралу
формулу Чебышева, будем иметь
![]() ,
,
где
![]() и
и
![]() - корни системы (8.13).
- корни системы (8.13).
В таблице приведены значения корней ti системы (8.12) для n=1,2…,7.
Таблица 8.1
Значения абсцисс ti в формуле Чебышева
|
n |
i |
ti |
|
2 |
2;1 |
±0.577350 |
|
3 |
3;1 2 |
±0.707107 0 |
|
4 |
4;1 3;2 |
±0.794654 ±0.187592 |
|
5 |
5;1 4;2 3 |
±0.832498 ±0.374541 0 |
|
6 |
6;1 5;2 4;3 |
±0.866247 ±0.422519 ±0.266635 |
|
7 |
7;1 6;2 5;3 4 |
±0.883862 ±0.529657 ±0.323912 0 |
Пример 8.3. Вычислить интеграл из предыдущего примера по формуле Чебышева для четырех и для пяти точек в Mathcad.

Оценить точность вычислений.

![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()




![]()
![]()
Рис. 8.3. Решение примера 8.2 в Mathcad
