
- •Введение
- •Глава 1. Погрешность результата численного решения задачи
- •1.1. Источники и классификация погрешностей
- •1.2. Абсолютная и относительная погрешности. Формы записи данных.
- •1.3. Вычислительная погрешность
- •Глава 2. Решение нелинейных уравнений
- •2.1. Отделение корней уравнения
- •2.1.1. Аналитический метод отделения корней
- •2.1.2. Графический метод отделения корней
- •2.2. Уточнение приближенных корней
- •2.2.1. Метод половинного деления
- •2.2.2 Метод хорд
- •2.2.3. Метод Ньютона – метод касательных
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Глава 3. Решения систем линейных алгебраических уравнений
- •3.1. Метод итераций
- •3.1.1. Оценка погрешности приближений процесса итераций
- •3.1.2. Приведение линейной системы к виду, удобному для итерации:
- •3.2. Метод Зейделя
- •3.3. Метод релаксаций
- •Глава 4. Решение систем нелинейных уравнений
- •4.1. Метод Ньютона для систем нелинейных уравнений
- •4.2. Распространение метода Ньютона на системы из n уравнений с n неизвестными
- •4.3. Метод итераций для систем нелинейных уравнений
- •4.4. Распространение метода итераций на системы из n уравнений с n неизвестными
- •Глава 5. Интерполяция
- •5.1. Постановка задачи интерполирования
- •5.2. Конечные разности
- •5.3. Интерполяционная формула Ньютона №1
- •5.4. Интерполяционная формула Ньютона №2
- •5.5. Интерполяционный многочлен Лагранжа
- •5.5.1. Вычисление лагранжевых коэффициентов
- •5.5.2. Схема Эйткина
- •5.5.3. Остаточный член формулы Лагранжа
- •5.6. Обратное интерполирование
- •5.6.1 Итерационные методы для обратного интерполирования
- •Глава 6. Аппроксимация функций с помощью сплайнов
- •6.1. Кубические сплайны
- •Глава 7. Методы обработки экспериментальных данных
- •7.1 Построение эмпирической формулы.
- •7.2. Метод выбранных точек (метод натянутой нити)
- •7.3 Метод средних
- •7.4. Метод наименьших квадратов
- •7.5. Метод выравнивания
- •7.6. Метод наименьших квадратов для полиномов
- •Глава 8. Численное интегрирование
- •8.1. Квадратурные формулы Ньютона-Котеса
- •8.1. Формула трапеций и ее остаточный член
- •8.2. Общая формула трапеций и ее остаточный член
- •8 .3 Формула Симпсона и ее остаточный член
- •8.4. Общая формула Симпсона и ее остаточный член
- •8.5. Формулы Ньютона-Котеса высших порядков
- •8.6. Квадратурная формула Чебышева
- •8.7. Квадратурная формула Гаусса
- •Глава 9. Приближенное решение обыкновенных дифференциальных уравнений
- •9.1. Аналитические методы
- •9.1.1. Метод последовательного дифференцирования
- •9.1.2. Метод последовательных приближений.
- •9.1.3 Метод неопределенных коэффициентов.
- •9.2. Численные методы
- •9.2.1. Метод Эйлера
- •9.2.2. Модифицированные методы Эйлера Первый улучшенный метод Эйлера
- •Второй улучшенный метод Эйлера
- •Третий улучшенный метод Эйлера
- •9.2.3. Метод Рунге-Кутта для уравнений первого порядка
- •Список литературы
5.5. Интерполяционный многочлен Лагранжа
Для произвольно заданных узлов интерполирования пользуются более общей формулой, так называемой интерполяционной формулой Лагранжа.
Пусть на отрезке
![]() даны n+1
различных значений аргумента:
даны n+1
различных значений аргумента:
![]() ,
и известны значения для функции
,
и известны значения для функции
![]() .
Нам нужно построить многочлен
.
Нам нужно построить многочлен
![]() .
.
Решим сначала
частную задачу, построив полином такой,
что
 .
.
Т.к. искомый полином
обращается в нуль в n
точках
![]() ,
то он имеет вид:
,
то он имеет вид:
![]() ,
()
,
()
где
![]() - постоянный коэффициент. Полагая
- постоянный коэффициент. Полагая
![]() в формуле и учитывая, что
в формуле и учитывая, что
![]() ,
получим:
,
получим:
![]() .
.
Отсюда
 .
.
Вернемся к выражению ():
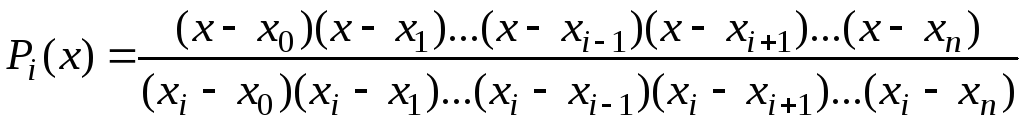 .
.
Тогда полином Лагранжа имеет следующий вид:
![]() .
.
Докажем единственность полинома Лагранжа.
Предположим
противное. Пусть
![]() - полином, отличный от
- полином, отличный от
![]() ,
степень его не выше n
и
,
степень его не выше n
и
![]() .
Тогда полином
.
Тогда полином
![]() ,
степень которого, очевидно, не выше n,
обращается в нуль в n+1
точках
,
степень которого, очевидно, не выше n,
обращается в нуль в n+1
точках
![]() ,
т.е.
,
т.е.
![]() .
Следовательно,
.
Следовательно,
![]() .
.
При равноотстоящих точках таблицы xi многочлен Лагранжа совпадает с многочленом Ньютона такой же степени.
5.5.1. Вычисление лагранжевых коэффициентов
 (5.2)
(5.2)
Можно записать
лагранжевы коэффициенты и более
компактно: 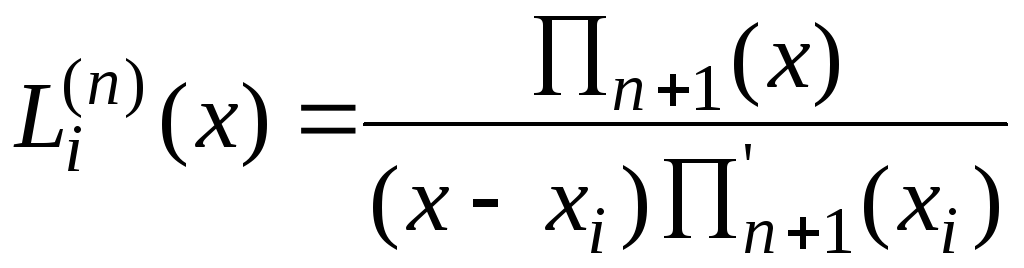 ,
(5.3)
,
(5.3)
где
![]() .
.
Формула Лагранжа
при этом имеет вид
![]() .
.
Для вычисления лагранжевых коэффициентов может быть использована приведенная ниже схема. Сначала располагаем в таблицу разности
Таблица 5.3.
Таблица разностей
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Обозначим
произведение элементов первой строки
через D0,
второй – D1
и т.д. Произведение же элементов главной
диагонали, очевидно, будет
![]() .
Отсюда следует, что
.
Отсюда следует, что
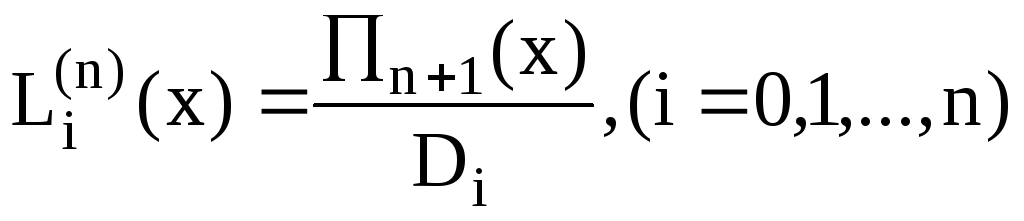 .Следовательно,
.Следовательно,
 .
.
Пример 5.3 Выполнено в Mathcad
Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лангранжа, если функция задана в неравно- отстоящих узлах таблицы.


Рис 5.2. Решения примера 5.3 в Mathcad
Отметим, что форма
лагранжевых коэффициентов инвариантна
относительно целой линейной подстановки
![]() (a,b
– постоянны ). Действительно, положив
в формуле (5.2):
(a,b
– постоянны ). Действительно, положив
в формуле (5.2):
![]() ,
, ![]() ,
,
![]() ,
,
после подстановки и сокращения числителя и знаменателя на an, получим:

или
 ,
,
где
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
В случае равноотстоящих точек лагранжевы коэффициенты могут быть приведены к более простому виду.
В самом деле,
полагая
![]() ,
будем иметь:
,
будем иметь:
![]() .
Отсюда
.
Отсюда
![]() и
и
![]() .
.
Тогда  ,
,
где
 .
Отсюда можно записать:
.
Отсюда можно записать:
 (5.4)
(5.4)
где
![]()
Пример 5.4 Выполно в Mathcad.
Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана в равноотстоящих узлах таблицы


Рис 5.3. Решения примера 5.4 в Mathcad
5.5.2. Схема Эйткина
Пусть требуется
найти не общее выражение
![]() ,
а лишь его значения при конкретных x.
При этом, значения функции даны в
достаточно большом количестве узлов,
тогда удобно пользоваться интерполяционной
схемой Эйткина. Согласно этой схеме
последовательно вычисляются многочлены:
,
а лишь его значения при конкретных x.
При этом, значения функции даны в
достаточно большом количестве узлов,
тогда удобно пользоваться интерполяционной
схемой Эйткина. Согласно этой схеме
последовательно вычисляются многочлены:
 .
.
Интерполяционный
многочлен степени «n»,
принимающий в точках xi
значения
![]() ,
запишется следующим образом:
,
запишется следующим образом:
 .
.
Вычисления по схеме Эйткина удобно расположить в такой таблице:
Таблица 5.4.
Вычисления по схеме Эйткина
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
… |
Вычисления по
схеме Эйткина обычно ведут до тех пор,
пока последовательные многочлены![]() и
и
![]() в таблице 5.4 не совпадут в пределах
заданной точности.
в таблице 5.4 не совпадут в пределах
заданной точности.
Пример 5.5
Функция
![]() задана таблицей
задана таблицей
|
|
|
|
1.0 |
1.000 |
|
1.1 |
1.032 |
|
1.3 |
1.091 |
|
1.5 |
1.145 |
|
1.6 |
1.170 |
Применяя схему
Эйткина, найти
![]() Составим таблицу 5.4 для примера:
Составим таблицу 5.4 для примера:
|
|
|
|
|
|
|
1.0 |
1.000 |
-0.15 |
|
|
|
1.1 |
1.032 |
-0.05 |
1.048 |
|
|
1.3 |
1.091 |
0.15 |
1.047 |
1.048 |
|
1.5 |
1.145 |
0.35 |
1.050 |
|
|
1.6 |
1.170 |
0.45 |
1.057 |
|
Значения
![]() и
и
![]() совпадают
до третьего знака. На этом вычисления
можно прекратить и с точностью до 0.001
записать
совпадают
до третьего знака. На этом вычисления
можно прекратить и с точностью до 0.001
записать
![]() =1.048
=1.048
