Тема 6. Кривые второго порядка
Рассмотрим
плоскость
.
К кривым 2-го порядка относятся линии,
описываемые многочленом от двух
пере-менных, максимальная степень
которого равна двум, то есть
,
.
Окружность
Окружностью
называется геометрическое место точек
плоскости, равноудаленных от некоторой
фиксированной точки
,
называемой ее центром.
Допустим, точка
лежит на данной окружности, то расстояние
СМ
равно некоторому числу R,
называемому радиусом этой окружности:
– уравнение
окружности
с центром в точке
и радиуса R.
Пример
6.1.
Найти центр и радиус окружности
.
Решение.
Выделим
полный квадрат по каждой перемен-ной,
данное уравнение можно записать в виде:
или
Следовательно,
это окружность с центром в точке
и радиусом
.
Эллипс
Эллипсом называется геометрическое место точек плос-кости, для которых сумма расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Выведем
уравнение эллипса. Пусть
и
– фокусы (рис. 6.1). Положим
.
Декартову систему координат зададим
следую-щим образом:
ось Ox
направим по прямой
,
а начало поместим
в середину отрезка
.
Тогда
,
.
Пусть
– произвольная точка эллипса. Тогда
,
где величина a
дана, причем
.
Имеем:
Следовательно, уравнение эллипса имеет вид:
.
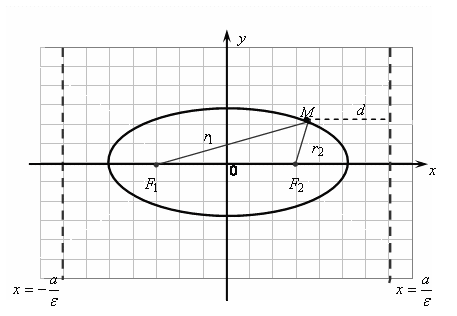
Рис. 6.1
Упростим последнее
равенство: перенесем второе слагаемое
в правую часть и возведем обе части в
квадрат, получим
,
после раскрытия скобок и приведения
подобных останется:
Разделим
полученное равенство
на четыре, возведем обе части еще раз в
квадрат:
и
преобразуем
.
После приведения подобных получим:
,
.
Обозначим
и разделим обе части последнего равенства
на эту величину:
– каноническое
уравнение эллипса
с полуосями
,
и центром симметрии в точке
.
Число
a
в уравнении эллипса называется большой,
а b
– малой полуосью эллипса. Прямую, на
которой расположены фокусы эллипса,
называют фокальной
осью.
Величина
называется эксцентриситетом
эллипса, а прямые
называются директрисами
эллипса.
Пример
6.2.
Доказать, что уравнение
определяет эллипс.
Решение.
Преобразуем уравнение, выделив полные
квадраты по каждой переменной,
Введем
новые переменные
,
.
Тогда
или
.
Последнее
уравнение определяет эллипс с центром
в точке
причем
,
.
Гипербола
Гиперболой
называется
геометрическое множество точек плоскости,
для которых абсолютная величина разности
расстояний до двух данных точек
и
этой плоскости, называемых фокусами,
есть величина постоянная, меньшая, чем
расстояние между фокусами.
Выведем уравнение
гиперболы. Положим
.
Систему координат (рис. 6.2) выберем так
же, как и в случае эллипса. Тогда
,
а
.
Если
– произвольная точка гиперболы, то
,
a
– постоянная,
.
Это уравнение соответствует определению
гиперболы. Преобразуя его, как и в случае
эллипса, и положив
,
получим каноническое
уравнение гиперболы:
.
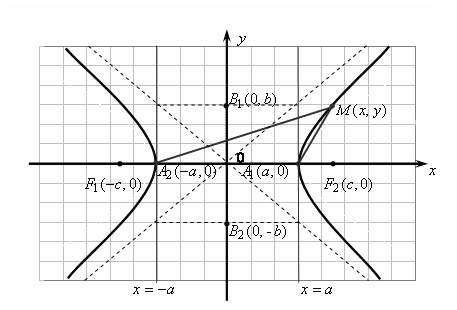
Рис. 6.2
Гипербола – кривая,
симметричная относительно осей и начала
координат. Прямые
являются асимптотами
гиперболы, величина
называется эксцентриситетом
гиперболы,
,
а прямые
– ее директрисами.