Парабола

Параболой называется геометрическое место точек плоскос-ти, равноудаленных от данной точки F и данной прямой (рис. 6.3). Точка F называется фокусом параболы, а данная прямая – директрисой параболы. Для получения уравнения параболы выберем систему координат следующим образом: ось Ox проведем через фокус F перпендикулярно директрисе. Начало координат поместим в точку, равноудаленную от фокуса и директрисы. Обозначим расстояние между фокусом и директрисой через p. Величина p называется параметром параболы. В выбранной системе координат фокус F имеет координаты , а уравнение директрисы имеет вид или .

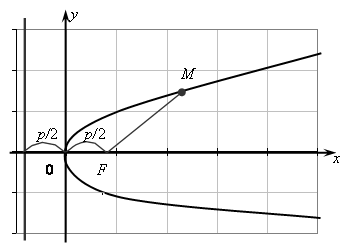
Рис. 6.3

Пусть – произвольная точка параболы. Соединим точку М с точкой F. Проведем отрезок MN перпендикулярно дирек-трисе. Согласно определению параболы, . По формуле расстояния между двумя точками находим: , а

Следовательно, .

После элементарных преобразований получим каноническое уравнение параболы:

.

Пример 6.3. Классифицировать линию 2-го порядка .

Решение. Воспользуемся формулой Выделим полный квадрат по каждой переменной, для этого сгруппируем отдельно слагаемые, содержащие переменную x и y: . Коэффициенты при пере-менных в старшей степени вынесем общими множителями . Полученные выражения в скобках доведем до полного квадрата, в первом случае прибавим и отнимем 25, во втором – 4: После раскрытия скобок постоянные пе-ренесем в правую часть равенства =Приведем подобные . Запишем уравнение линии 2-го порядка в общем виде. Разделим последнее равенство на 36, чтобы получить единицу в правой части

или .

Данная линия (рис. 6.4) является гиперболой с центром в точке и полуосями , .

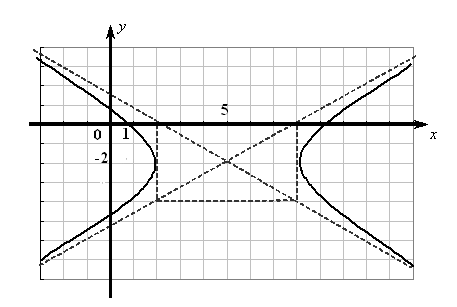
Рис. 6.4

Тема 7. Аналитическая геометрия в пространстве Уравнение поверхности и линии в пространстве

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О есть геометрическое место всех точек пространства, находящихся от точки О на расстоянии R.

Прямоугольная система координат Оxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел x, y и z – их координатами: абсциссой, ординатой и аппликатой. Коорди-натами точки в пространстве (рис. 7.1) являются числа, соответствующие точкам пересечения координатных плоскостей Oxy, Oxz, Oyz с координатными осями Ox, Oy, Oz.

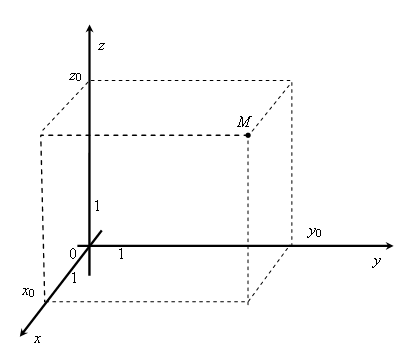
Рис. 7.1

Свойство, общее для всех точек поверхности, можно запи-сать в виде уравнения, связывающего координаты всех точек поверхности [2].

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение с тремя переменными, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные x, y и z в уравнении поверхности называются текущими координатами точек поверхности. Линию в пространстве можно рассматривать как линию пересечения двух поверхностей или как геометрическое место точек, принадлежащее обеим поверхностям.

Если и – уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными: 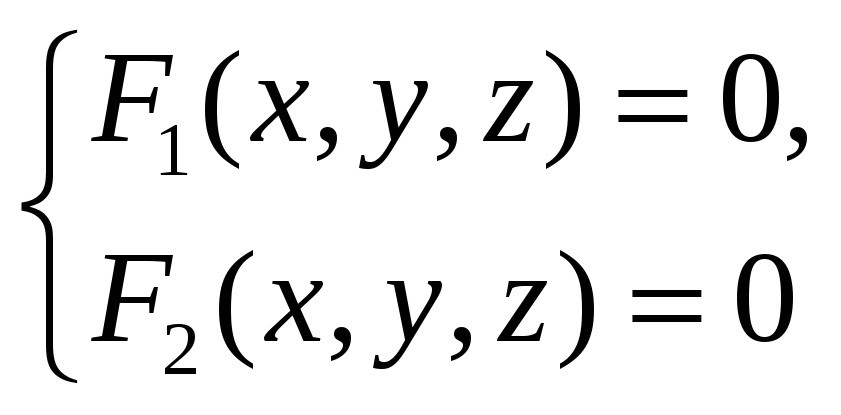– уравнение линии в пространстве.

Например, есть уравнение оси Оz.

Линию в пространстве можно задать как траекторию движения некоторой точки. В этом случае ее задают векторным уравнением или параметрическими уравнениями: , , .