Числовые последовательности

Определение. Функция f целочисленного аргумента n: называется числовой последовательностью

где – общий член последовательности. Числовую пос-ледовательность можно записать более компактно:

, или .

Замечание. Числовая последовательность всегда состоит из счетного (бесконечного) числа членов, поскольку любую «конечную» последовательность можно представить в виде

.

Это обусловлено тем, что «конечные» последовательности не представляют теоретического интереса.

Определение. Числовая последовательность называ-ется ограниченной, если существует число K, такое, что любой член этой последовательности по абсолютной величине не пре-восходит этого числа, то есть



Аналогично числовая последовательность называется не-ограниченной, если для любого фиксированного числа K существует такой номер , что всякий член этой последова-тельности по абсолютной величине больше этого числа, то есть , Þ .

Предел числовой последовательности

Определение. Число a называется пределом последовательнос-ти , если для любого сколь угодно малого существует та-кое число , вообще говоря, зависящее от e, что для всех натураль-ных n, больших выполняется неравенство , то есть Þ . Для вычисления предела последовательности используется обозначение (или ).

Определение. Окрестностью точки , , последова-тельности называется любой открытый интервал, содержащий .

Определение. Число a называется пределом последователь-ности , если в любой его окрестности содержится бесконечное число членов последовательности.

Заметим, что окрестность числа a не обязана содержать это число, в этом случае говорят о выколотой окрестности числа а.

Пример 8.3. Пусть задана числовая последовательность . Докажем, что .

Решение. Общий член последовательности . Вос-пользуемся определением и найдем такое число , что для любого малого и натурального выполняется неравенство: . Разрешим это неравенство относительно n: , так как , то модуль автоматически опускается, и получаем Þ . Таким образом, найдено такое, что выполняется неравенство , то есть .

В обозначениях через «lim» вычисление предела осуществляется по схеме:

.

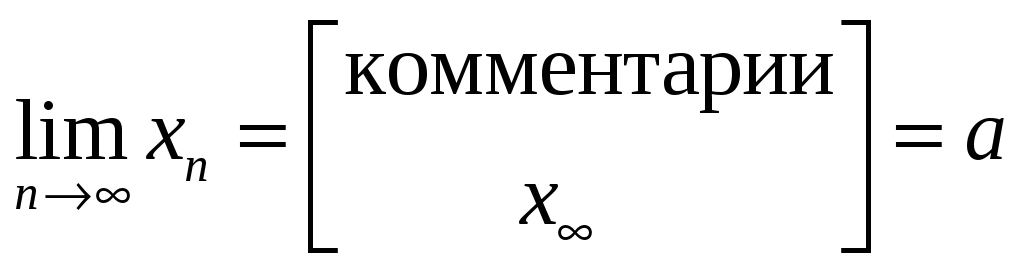В нашем случае:

.

Замечание. Из определения следует, что последовательность имеет предел, если, начиная с некоторого номера то есть при , все элементы последовательности попадают в интервал который называется e-окрестностью точки а.

Определение. Последовательность называется бес-конечно малой, если :  , то есть .

Свойства бесконечно малых

1. Сумма бесконечно малых есть бесконечно малая.

2. Произведение бесконечно малой на ограниченную ве-личину есть бесконечно малая.

Теорема 8.1. Для того чтобы последовательность имела пре-дел, равный a, необходимо и достаточно, чтобы , , где , – бесконечно малая последовательность.

Определение. Последовательность называется бес-конечно большой, если  , то есть .

Определение. Последовательность называется схо-дящейся, если она имеет конечный предел.