
- •С.А. Иванова, в.А. Павский Математика
- •Часть 1
- •Оглавление
- •Тема 10. Исследование функции 145
- •Введение
- •Тема 1. Элементы линейной алгебры Матрицы и действия над ними
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •Определитель матрицы
- •Свойства определителей
- •Вычисление определителей
- •Обратная матрица
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •Тема 2. Системы линейных алгебраических уравнений
- •Методы решения системы линейных алгебраических уравнений
- •1. Метод Крамера
- •2. Матричный метод
- •3. Метод Гаусса
- •Однородная система линейных алгебраических уравнений
- •Системы линейных неравенств
- •Тема 3. Линейные пространства
- •Базис линейного пространства
- •Собственные значения и собственные векторы матрицы
- •Тема 4. Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Проекция вектора на ось
- •Разложение вектора по ортам координатных осей
- •Модуль вектора. Направляющие косинусы
- •Базис системы векторов
- •Скалярное произведение векторов
- •Cвойства скалярного произведения
- •С помощью скалярного произведения находят
- •Векторное и смешанное произведение векторов
- •Свойства векторного произведения
- •Свойства смешанного произведения
- •Тема 5. Аналитическая геометрия на плоскости Система координат на плоскости
- •Уравнение линии на плоскости
- •Уравнение прямой на плоскости
- •Тема 6. Кривые второго порядка
- •Окружность
- •Гипербола
- •Парабола
- •Тема 7. Аналитическая геометрия в пространстве Уравнение поверхности и линии в пространстве
- •Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей
- •Уравнение прямой в пространстве
- •Уравнения прямой, проходящей через две данные точки
- •Деление отрезка в данном отношении
- •Тема 8. Функции. Теория пределов Понятие функции
- •Способы задания функции
- •Графический
- •Элементарные функции
- •Задание функций в полярной системе координат
- •Числовые последовательности
- •Предел числовой последовательности
- •Свойства бесконечно малых
- •Свойства сходящихся последовательностей
- •О сжатой последовательности
- •Предел функции
- •Основные теоремы о пределах
- •Вычисление пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Эквивалентные функции
- •Непрерывность функции
- •Классификация точек разрыва
- •Тема 9. Дифференциальное исчисление Определение производной
- •Геометрический смысл производной
- •Правила дифференцирования, таблица производных
- •Правила дифференцирования
- •Производные сложной и обратной функций
- •Дифференцирование неявных и параметрически заданных функций
- •Логарифмическое дифференцирование
- •Геометрические приложения производной
- •Дифференциал функции
- •Основные свойства дифференциала
- •Производные высших порядков
- •Теоремы о дифференцируемости функции
- •Правило Лопиталя
- •Формула Тейлора
- •Тема 10. Исследование функции Возрастание и убывание функции
- •Экстремумы функции
- •Наибольшее и наименьшее значения функции
- •Вогнутость и выпуклость функции. Точки перегиба
- •Асимптоты графика функции
- •Заключение
- •Задания для самостоятельной работы
- •Список литературы
- •Математика
- •Часть 1 Нач. Редакции а.С. Обвинцева
- •650010, Г. Кемерово, ул. Красноармейская, 52
Свойства сходящихся последовательностей
-
Если для последовательности
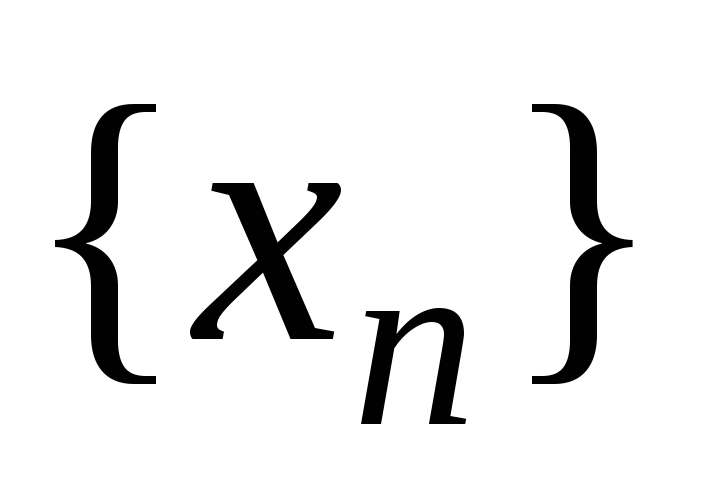 существует предел, равный a,
и число
существует предел, равный a,
и число
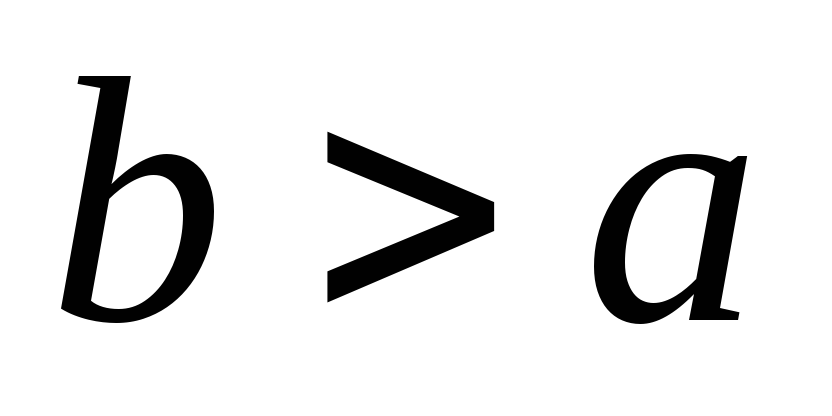 (или
(или
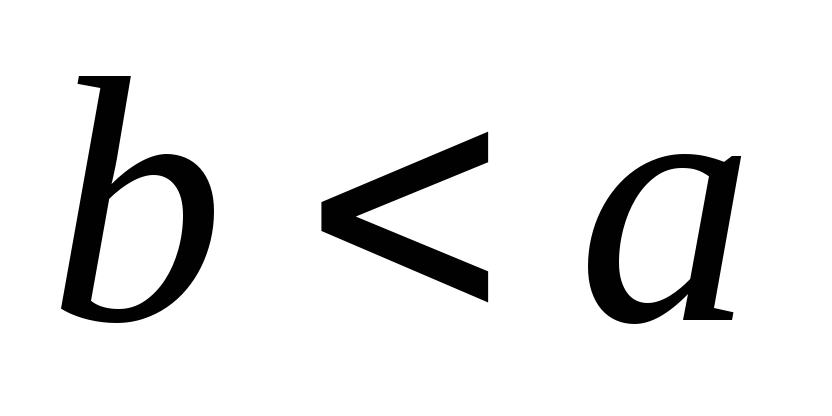 ),
то существует такое число N,
что для
любого
),
то существует такое число N,
что для
любого
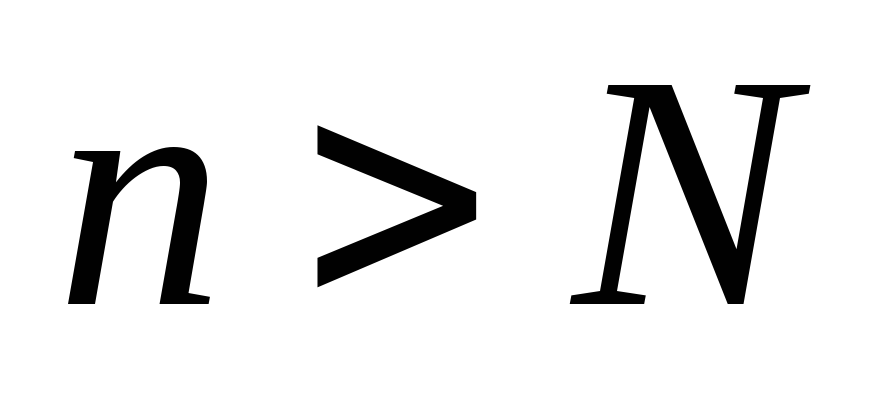 следует, что
следует, что
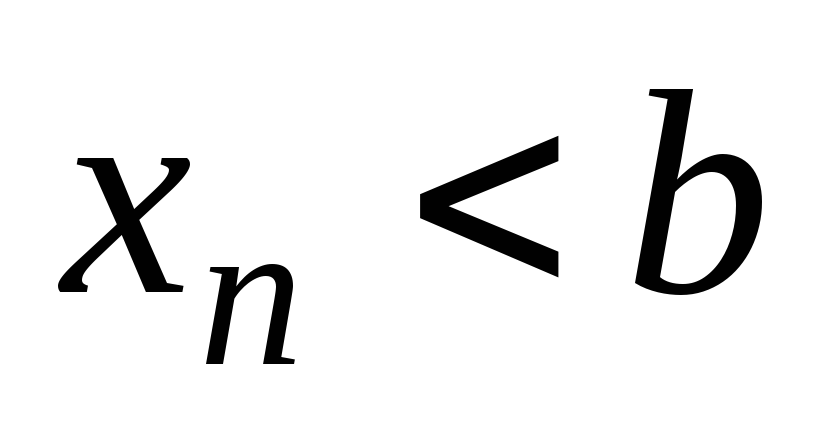 (или
(или
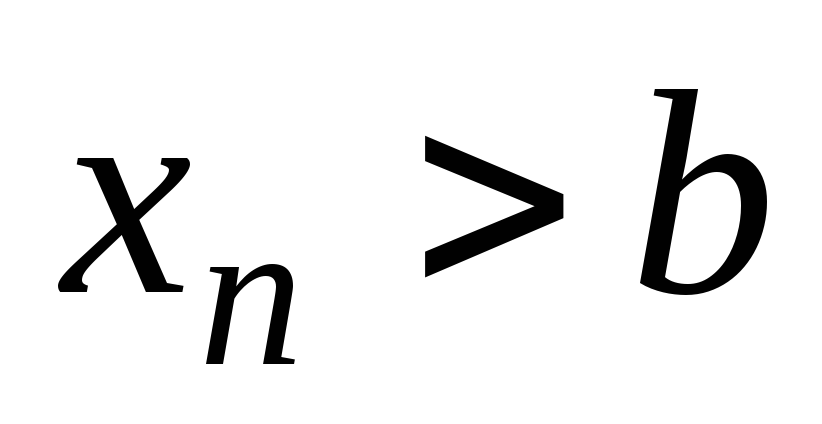 ).
).
Следствие.
Если для последовательности
![]() сущест-вует предел, равный a,
и
сущест-вует предел, равный a,
и
![]() (или
(или
![]() ),
то
),
то
![]()
![]() (или
(или
![]() ).
).
-
Если для последовательности
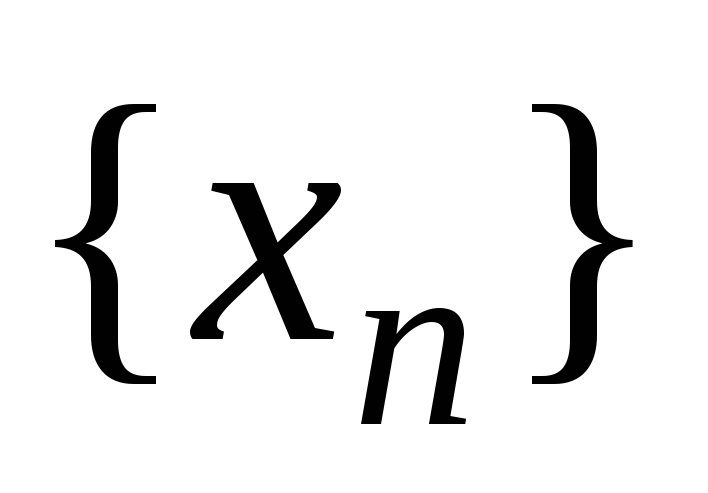 существует предел, равный a,
и для любого номера n,
существует предел, равный a,
и для любого номера n,
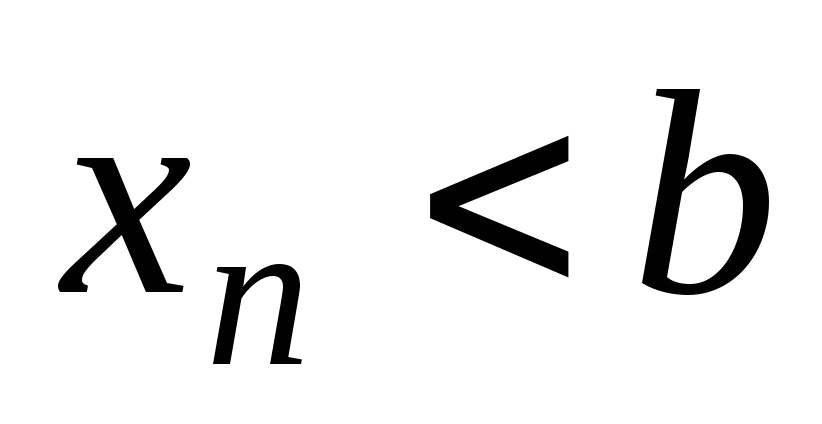 или
или
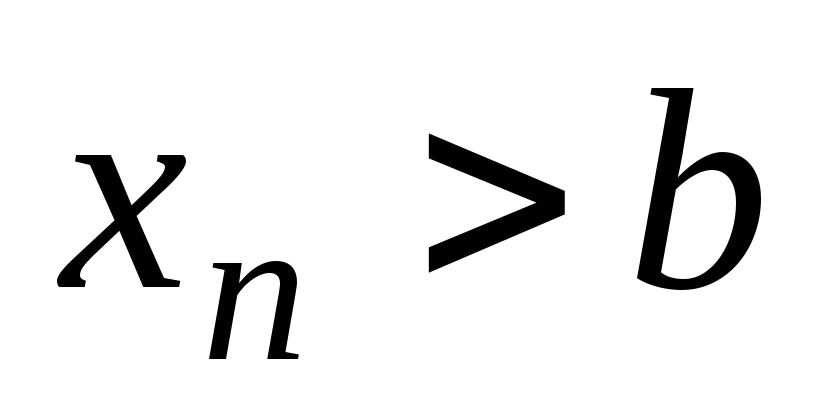 ,
то
,
то
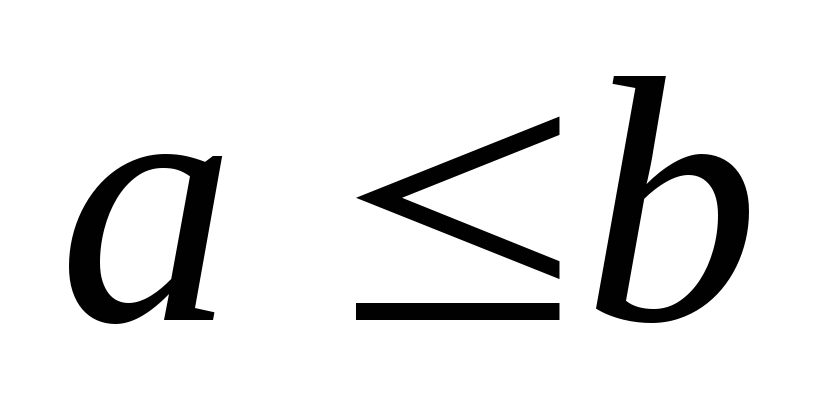 или
или
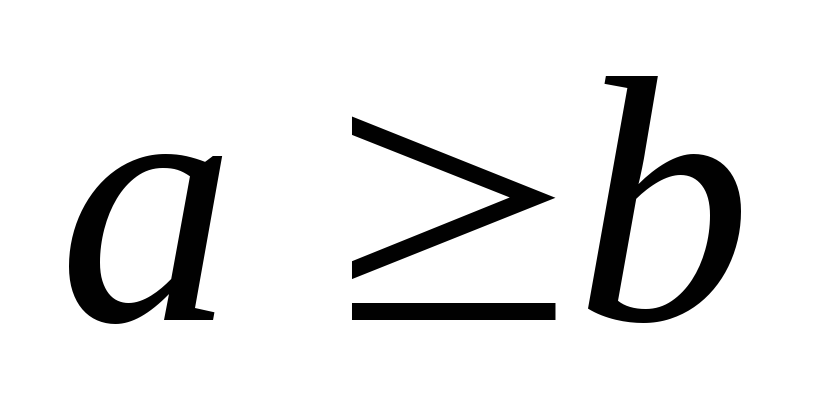 .
. -
Если для последовательностей
 и
и
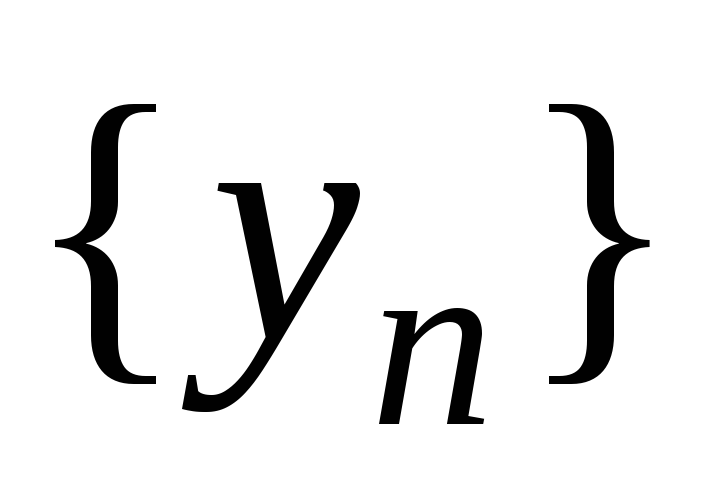 сущест-вуют пределы, равные соответственно
a
и b,
и для любого номе-ра n
выполняется неравенство
сущест-вуют пределы, равные соответственно
a
и b,
и для любого номе-ра n
выполняется неравенство
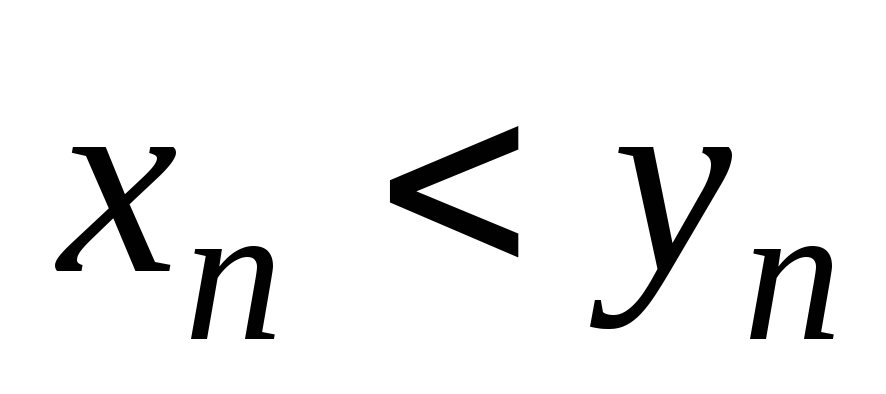 ,
то
,
то
 .
.
О сжатой последовательности
-
Пусть заданы три последовательности
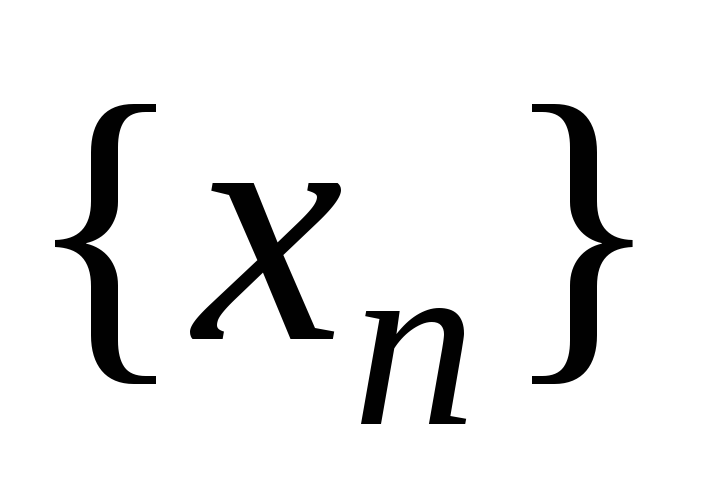 ,
,
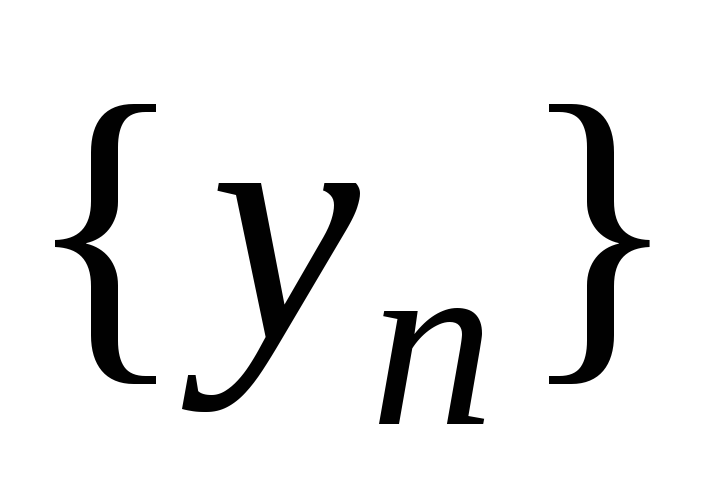 ,
,
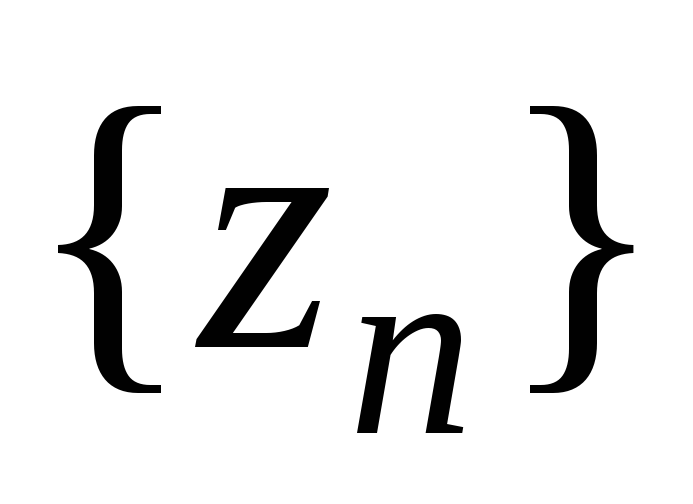 ,
для которых выполняется условие: для
любого номера n
,
для которых выполняется условие: для
любого номера n
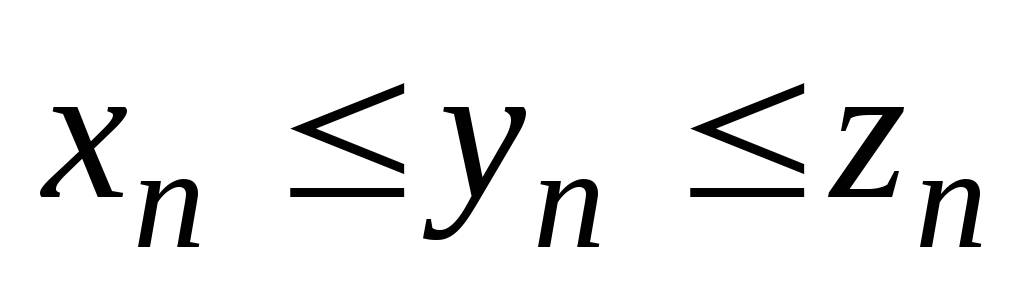 .
Тогда если последовательности
.
Тогда если последовательности
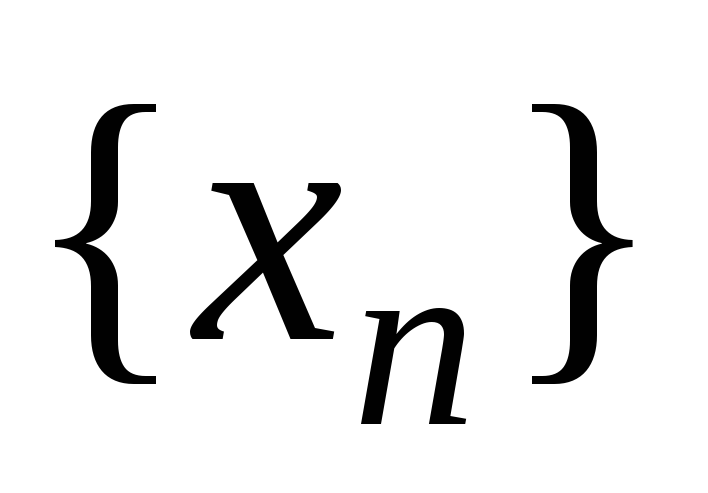 и
и
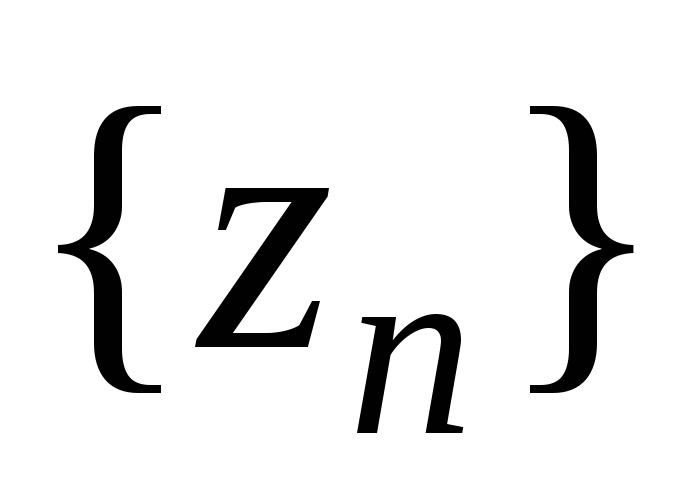 имеют предел, равный a,
то и последовательность
имеют предел, равный a,
то и последовательность
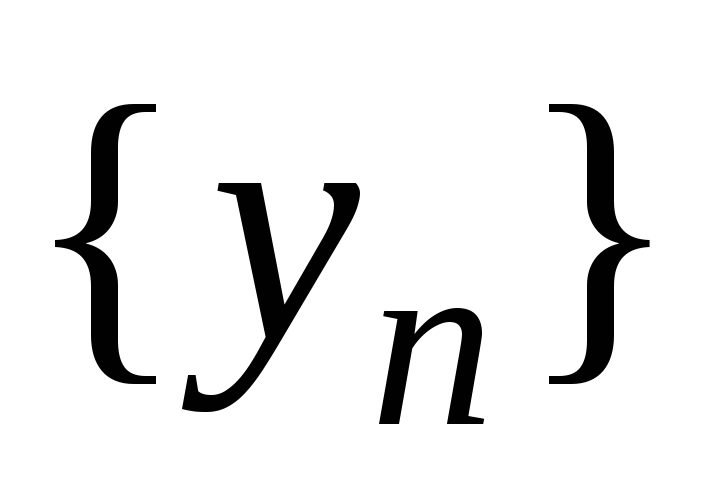 имеет предел, равный a.
имеет предел, равный a. -
Если для последовательности
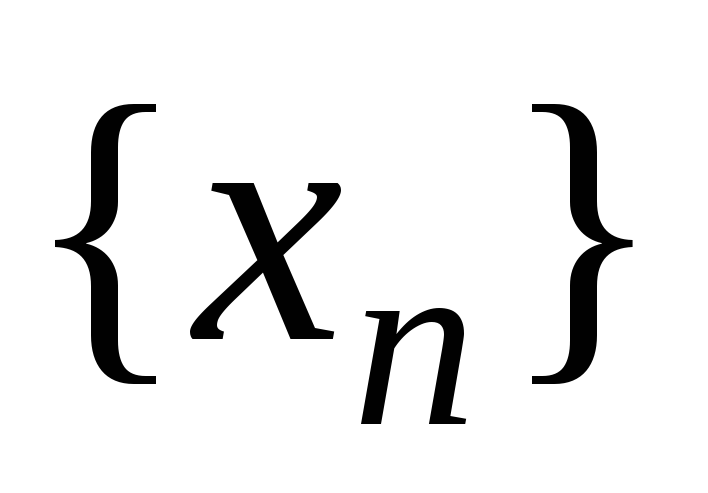 существует предел, то он единственный.
существует предел, то он единственный. -
Если для последовательности
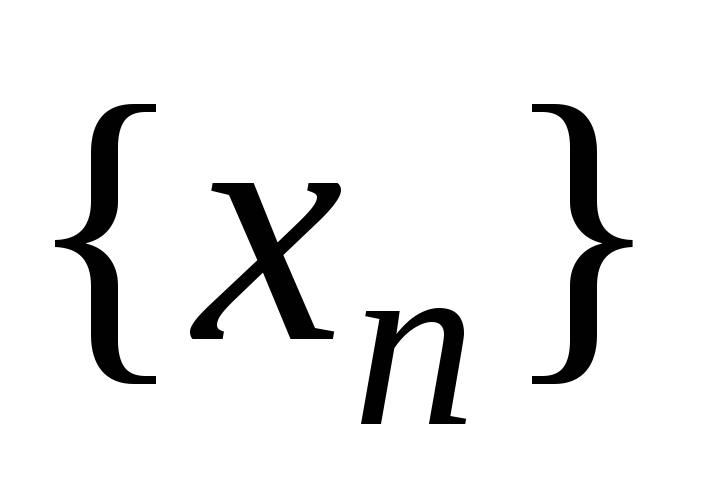 существует предел, то она ограничена.
существует предел, то она ограничена.
Пример 8.4. Вычислим пределы:
1)
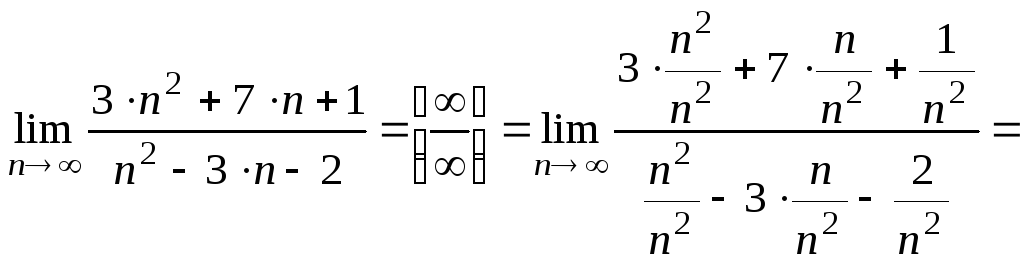
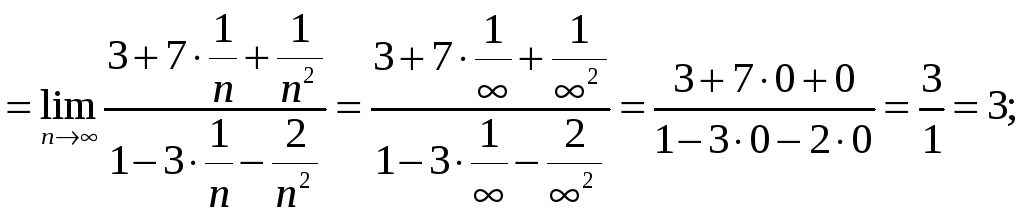
2)
![]() ;
;
3)
![]()
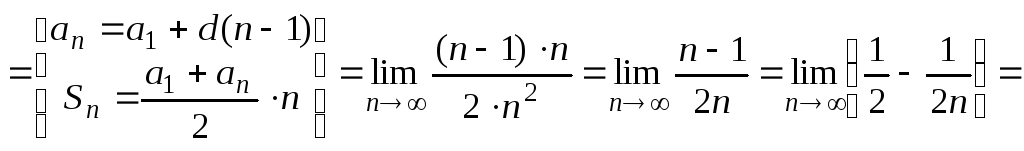
![]() ;
;
4)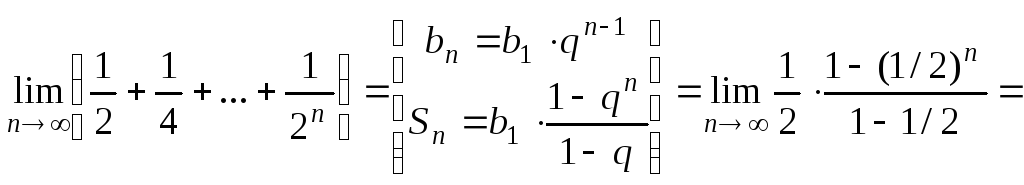
![]() .
.
Определение.
Последовательность
![]() называется моно-тонно возрастающей
(или монотонно убывающей) при возрас-тании
n,
если
называется моно-тонно возрастающей
(или монотонно убывающей) при возрас-тании
n,
если
![]()
![]() (или
(или
![]() ).
).
Последовательность
![]() называется неубывающей (или невозрастающей),
если
называется неубывающей (или невозрастающей),
если
![]()
![]() (или
(или
![]() ).
).
Определение.
Число a
является верхней (или нижней) гранью
последовательности
![]() ,
если:
,
если:
-
для всех
 выполняется неравенство
выполняется неравенство
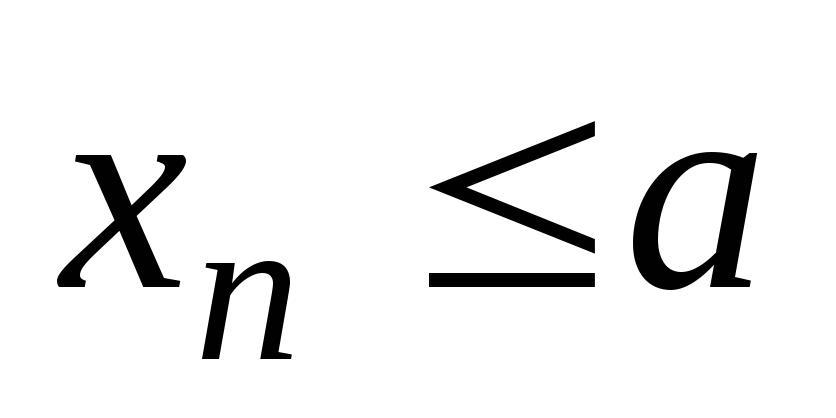 (или
(или
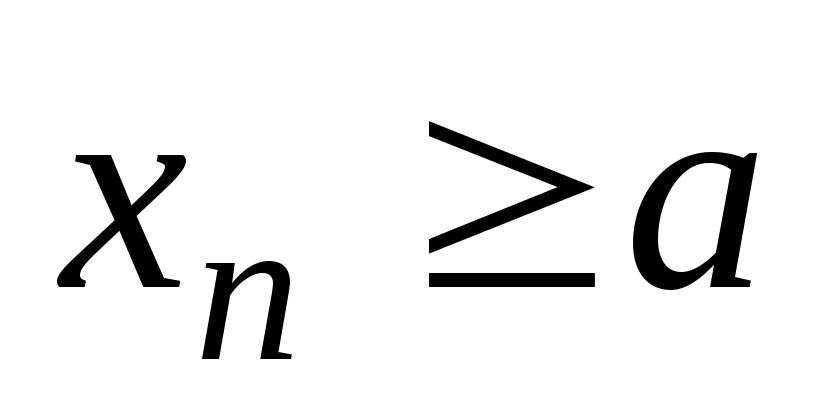 );
); -
для любого
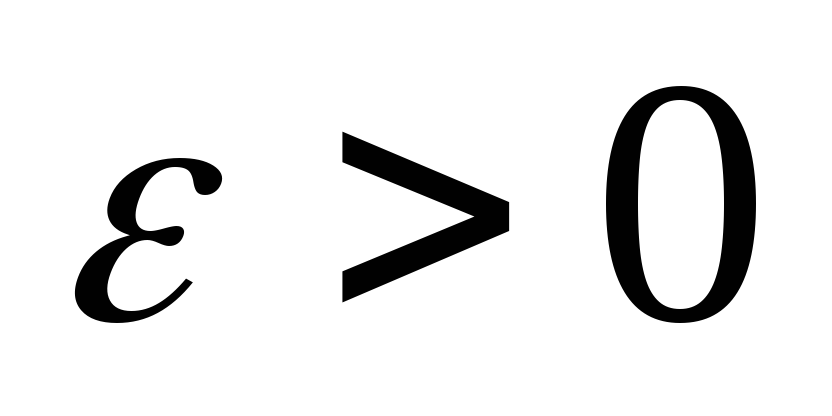 существует такой номер
существует такой номер
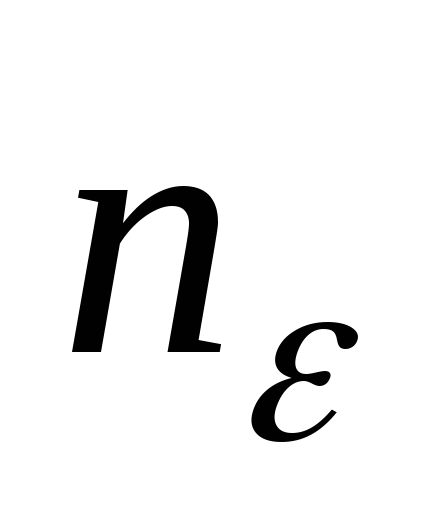 ,
что
,
что
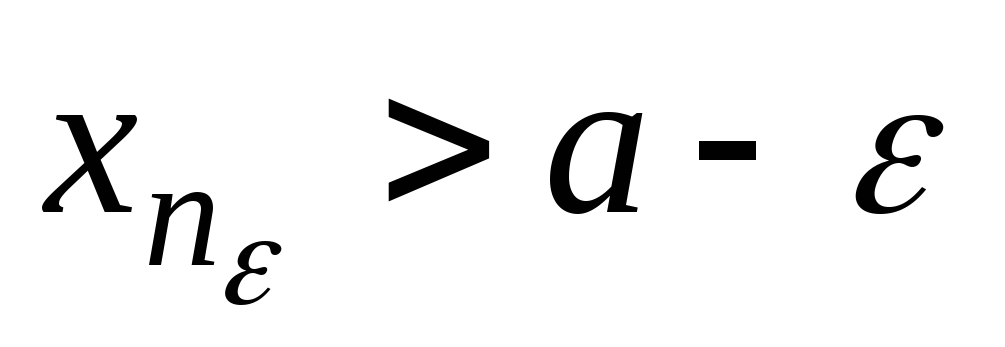 (соответственно
(соответственно
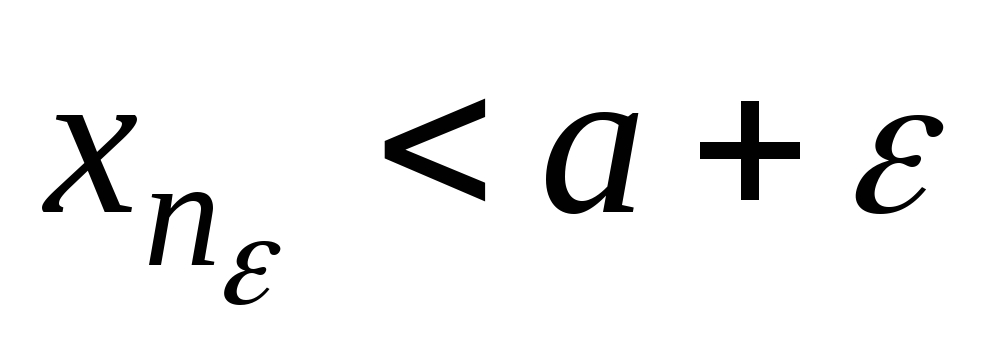 )
и обозначается
)
и обозначается
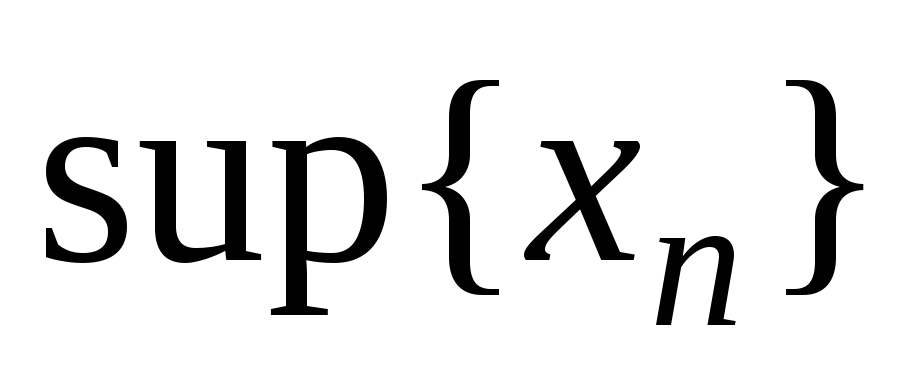 (или
(или
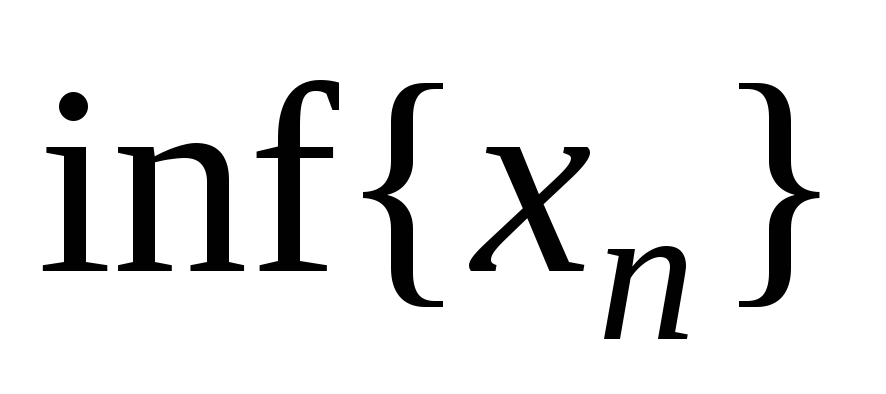 ).
).
Теорема 8.2.
Если последовательность
![]() монотонно возрастает (монотонно убывает)
и ограничена сверху (снизу), то она имеет
предел, равный
монотонно возрастает (монотонно убывает)
и ограничена сверху (снизу), то она имеет
предел, равный
![]() (
(![]() ).
).
Пример 8.6.
Рассмотрим
последовательность
![]() ,
,
![]() .
Покажем, что она монотонно возрастает
и ограничена сверху.
.
Покажем, что она монотонно возрастает
и ограничена сверху.
Решение. Воспользуемся формулой бинома Ньютона:
![]()
![]() ,
,
где
![]() – число сочетаний из n
элементов по k
элементов [4],
– число сочетаний из n
элементов по k
элементов [4],
![]() ,
,
![]()
Определение.
Произведение натуральных чисел 1, 2, …,
n
называется эн-факториалом
и обозначается символом
![]() ,
то есть
,
то есть
![]()
При
этом
![]() ,
,
![]() ,
по определению
,
по определению
![]()
Далее, учитывая определение числа сочетаний, имеем
![]()
![]() .
.
Пусть
![]() ,
,
![]() ,
тогда
,
тогда
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]() .
.
Так как
![]()
![]() ,
то
,
то
![]() Þ
Þ
Þ
![]() ;
;
![]() Þ
Þ
![]() ;
;
……………………………………
![]() Þ
Þ
![]() .
.
Кроме того,
![]() содержит на одно слагаемое больше,
поэтому
содержит на одно слагаемое больше,
поэтому
![]()
![]() ,
то есть последовательность моно-тонно
возрастающая.
,
то есть последовательность моно-тонно
возрастающая.
Ограничим
ее сверху: так как
![]()
![]() ,
,
![]() ,
…,
,
…,
![]() и
и
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() ,
то
,
то
![]()
![]() .
.
То
есть
![]()
![]() ,
тогда по теореме о монотонно возрастающей
ограниченной последовательности для
нашей после-довательности предел
существует, обозначим его числом e,
тогда
,
тогда по теореме о монотонно возрастающей
ограниченной последовательности для
нашей после-довательности предел
существует, обозначим его числом e,
тогда
![]() .
Замечая, что
.
Замечая, что
![]() ,
,
![]() ,
,
![]()
![]() ,
…, получим,
что
,
…, получим,
что
![]() .
Это трансцендентное число имеет такую
же значимость в матема-тике, как и число
p
[3].
Иначе говоря,
.
Это трансцендентное число имеет такую
же значимость в матема-тике, как и число
p
[3].
Иначе говоря,
![]() .
.
Предел функции
Понятие предела является одним из основных в функциональном анализе [3]. С помощью предела формулируется множество других более общих понятий. Большинство новых утверждений и результаты в анализе получены благодаря понятию предела.
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
![]() .
.
Определение.
Число
А
называется пределом
функции
![]() при
при
![]() ,
если для любого сколь угодно малого
,
если для любого сколь угодно малого
![]() существует
существует
![]() ,
что, как только
,
что, как только
![]() ,
так сейчас же
,
так сейчас же
![]() .
Через кванторы всеобщности ()
и существования ()
предел функции запишется формулой
.
Через кванторы всеобщности ()
и существования ()
предел функции запишется формулой
![]()
![]()
![]()
![]() или, что то же самое,
или, что то же самое,
![]()
Определение.
e-Окрестностью
точки
![]() называется любой открытый интервал с
центром в точке
называется любой открытый интервал с
центром в точке
![]() радиуса e:
радиуса e:
![]()
Определение.
Число
А
называется пределом
функции
![]() при
при
![]() ,
если для любого x,
принадлежащего -окрестности
точки
,
если для любого x,
принадлежащего -окрестности
точки
![]() ,
значения функции
,
значения функции
![]() принадлежат -окрестности
числа A,
где
принадлежат -окрестности
числа A,
где
![]() –
сколь угодно малое число, вообще говоря,
зависящее от e.
Окрестность
числа A
может быть выколотой.
–
сколь угодно малое число, вообще говоря,
зависящее от e.
Окрестность
числа A
может быть выколотой.
Определение.
Функция
![]() называется бесконечно малой функцией
при
называется бесконечно малой функцией
при
![]() ,
если для любого малого
,
если для любого малого
![]() существует такая d-окрестность
точки
существует такая d-окрестность
точки
![]() ,
что
,
что
![]() ,
то есть
,
то есть
![]()
![]() (
(![]() )
)
![]() ,
что эквивалентно записи
,
что эквивалентно записи
![]()
Определение.
Функция
![]() называется бесконечно большой функцией
при
называется бесконечно большой функцией
при
![]() ,
если для любого малого
,
если для любого малого
![]() существует
d-окрестность
точки
существует
d-окрестность
точки
![]() такая, что
такая, что
![]() ,
то есть
,
то есть
![]()
![]() (
(![]() )
(
)
(![]() )
или
)
или
![]() .
.
Замечание.
Символ «»
является абстракцией, поэтому символы
«+»
или «–»
следует рассматривать как бесконечно
удаленные точки на числовой оси. Совпадают
ли они в «бесконечности» или находятся
на противоположных сторонах – неизвестно.
Все зависит от их физической интерпретации
и от правил действия с числами разных
знаков. Под бесконечно большой величиной
следует понимать любую функцию
![]() ,
которая при
,
которая при
![]() находится от любого конечного числа
находится от любого конечного числа
![]() на сколь угодно большом расстоянии.
на сколь угодно большом расстоянии.
Теорема 8.3. Функция, обратная к бесконечно малой, есть бесконечно большая функция, и наоборот, то есть
![]() ;
;
![]() .
.
