Производные сложной и обратной функций

Теорема 9.1. Производная сложной функции или где равна произведению производной функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной x:

или .

Пример 9.3. Найти производную функции:

1) ; 2) .

1. Представим данную функцию как степенную 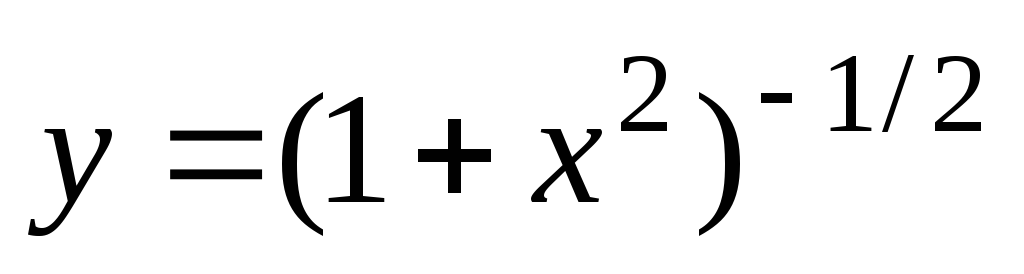и найдем ее производную: .

2. .

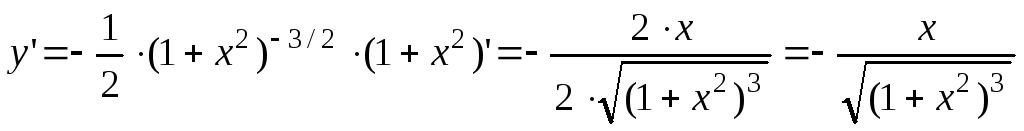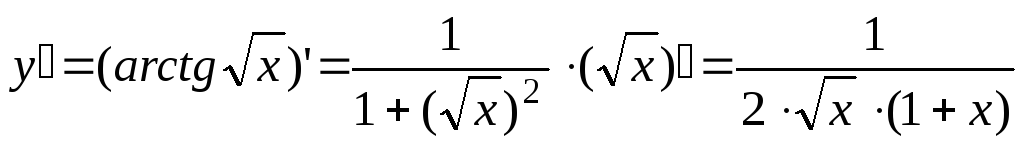Определение. Пусть функция определена на множестве X со значениями из множества Y. Функция, определенная на Y и сопоставляющая значению такое , что , называется обратной для функции и обозначается , (то есть ).

Для существования на функции, обратной к , не-обходимо, чтобы была строго монотонна, то есть : или , или .

Теорема 9.2. Если функция строго монотонна на интервале и имеет производную в каждой точке этого интервала, то обратная к ней функция существует и имеет производную в соответствующей точке, определяемую по формуле или .

Таким образом, производная обратной функции равна обратной величине производной данной функции.

Пример 9.4. Найти производную функции , .

Решение. Обратной к функции является функ-ция , , тогда .

Тогда по теореме о дифференцировании обратной функции имеем:

.

Дифференцирование неявных и параметрически заданных функций

Если неявная функция задана уравнением , то для нахождения производной от y по x нет необходимости разрешать уравнение относительно y: достаточно продиф-ференцировать это равенство по x, рассматривая при этом y как функцию x, и затем полученное равенство разрешить отно-сительно y’. Производная неявной функции выражается через аргумент x и функцию y.

Пример 9.5. Найти производную функции, заданную уравнением .

Решение. Функция задана неявно. Дифференцируем по x данное равенство.

Из полученного соотношения следует, что , то есть .

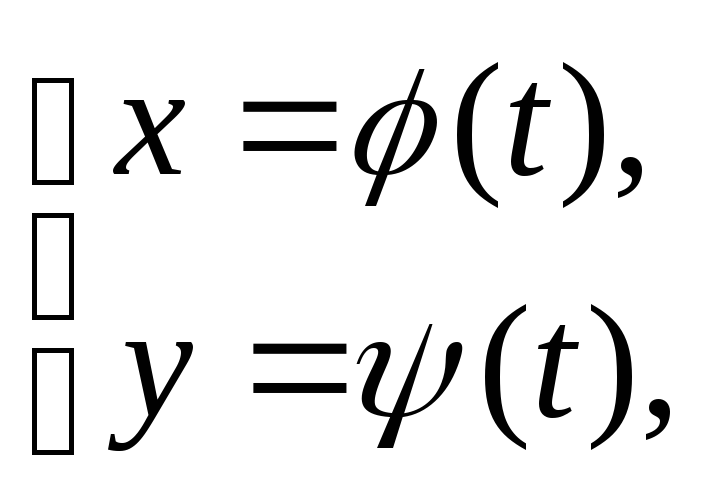
Пусть функция задана параметрически , где функции , – дифференцируемые и .

Найдем производную , считая, что функция имеет обратную . По правилу дифференцирования обратной функции имеем:

. (18)

По правилу дифференцирования сложной функции получаем: , то есть .

Полученная формула позволяет находить производную от функции, заданной параметрически, не находя явной зависи-мости функции y от x.

Пример 9.6. Пусть Найти .

Решение. Имеем , . По формуле (18) имеем .

Логарифмическое дифференцирование

Логарифмическое дифференцирование состоит в том, что первоначально заданную функцию логарифмируют, а затем приступают к дифференцированию, помня, что y является функ-цией аргумента x.

Логарифмическое дифференцирование целесообразно исполь-зовать в случаях, когда взятие производной существенно упрощается после логарифмирования исходной функции (сложно-показательных функций сложных дробно-рациональных функций и т. п.) и приводит к неопределенному выражению .

Найдем производную функции , где , – дифференцируемые функции. Для этого ее прологарифмируем с целью упрощения последующих вычислений по основанию e: . Дифференцируем обе части последнего равенства по х: получаем:

; ;

Окончательно имеем .

Пример 9.7. Найти производную функции .

Решение. Учитывая вышесказанное, получаем ,

дифференцируем ;.

Окончательно имеем .

Пример 9.8. Найти производную функции

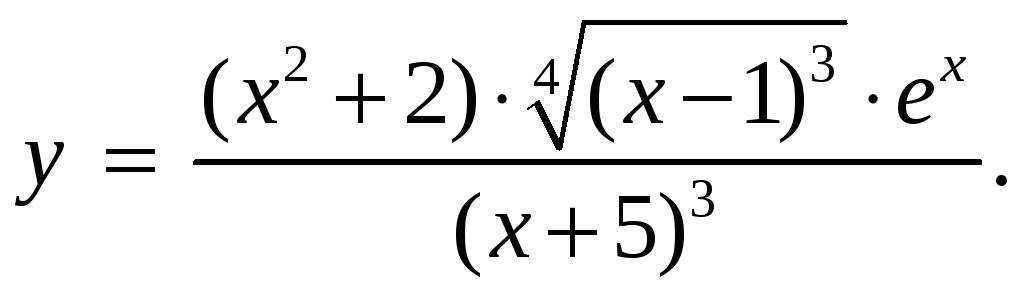
Решение. Прологарифмируем заданную функцию , продифференцируем полученное равенство как неявно заданную функцию x:

.

Выражаем : ,

то есть

.