Уравнение плоскости в пространстве

Рассмотрим трехмерное пространство с фиксированной декартовой системой координат Oxyz.

Координатная плоскость Oxy в нем является подпространством размерности два. Изученная нами прямая и кривые 2-го порядка, лежащие в плоскости Oxy, в пространстве также могут быть определены. Для этого необходимо задать саму плоскость Oxy в нем.

Очевидно, что если в пространстве задана система координат Oxyz, то плоскость Oxy определяется в ней уравнением .

Но плоскость в пространстве в системе координат может быть определена по-разному, поскольку она не обязательно долж-на проходить через начало или быть перпендикулярной другим ко-ординатным плоскостям.

Естественно возникает вопрос об уравнении плоскости в пространстве.

Справедливы утверждения:

1. Если в пространстве (размерности 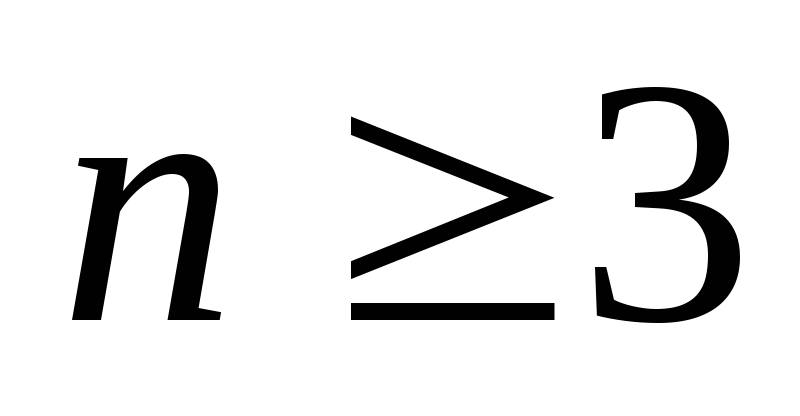) задана произвольная плоскость и фиксирована произвольная декартовая система координат Oxyz, то плоскость определяется в ней уравнением 1-й степени.

2. Если в пространстве (размерности 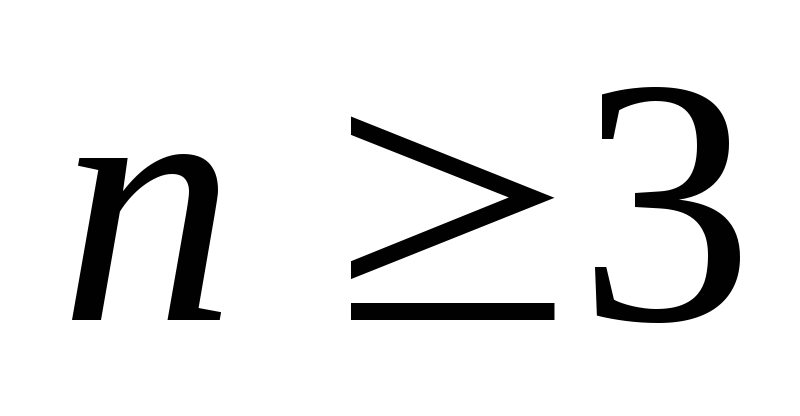) фикси-рована произвольная декартовая прямоугольная система коор-динат Oxyz, то всякое уравнение 1-й степени с переменными x, y, z определяет в ней плоскость.

Ниже мы эти утверждения сформулируем в виде теорем.

Пусть Р – произвольная плоскость в пространстве. Всякий перпендикулярный ей ненулевой вектор называется нормальным вектором этой плоскости (рис. 7.2).

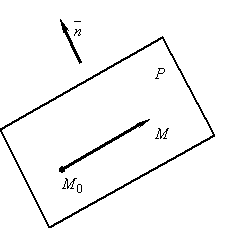
Рис. 7.2

Если известна какая-нибудь точка плоскости P и какой-нибудь ее нормальный вектор , то этими двумя условиями плоскость в пространстве вполне определена (через данную точку можно провести единственную плоскость, перпендикулярную данному вектору).

В самом деле, возьмем на плоскости P произвольную точку М с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору , а для этого необходимо и достаточно, чтобы скалярное произведение этих векторов равнялось нулю, то есть .

Вектор задан по условию, найдем координаты вектора: и запишем скалярное произведение этих векторов в координатной форме:

. (12)

Так как точка выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости Р. Для точки N, не лежащей на заданной плоскости, и равенство (12) нарушается. Следовательно, уравнение (12), являясь уравнением 1-й степени, определяет плоскость, проходящую через точку и пер-пендикулярную вектору

Пример 7.1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Решение. Используя формулу (12), имеем откуда после преобразований получим .

Это уравнение 1-й степени и есть искомое уравнение плоскости.

Уравнение плоскости, проходящей через три точки. Пусть даны три точки , и . Если точки не лежат на одной прямой, то через них всегда можно провести единственную плоскость. Обозначим (х, у, z) координаты произвольной точки М пространства и рассмотрим три вектора: , , . Точка М лежит на плоскости М₁М₂М₃ в том и только в том случае, когда перечисленные три вектора компланарны, а значит, , т. е. определитель, составленный из их координат, равен нулю:

.

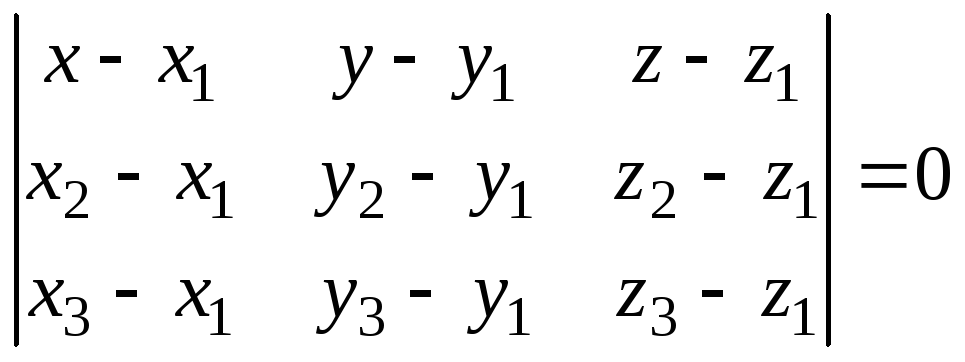Пример 7.2. Написать уравнение плоскости, проходящей через точки , и

Решение. Пусть – произвольная точка плоскости, тогда векторы , , компланарны, поэтому:

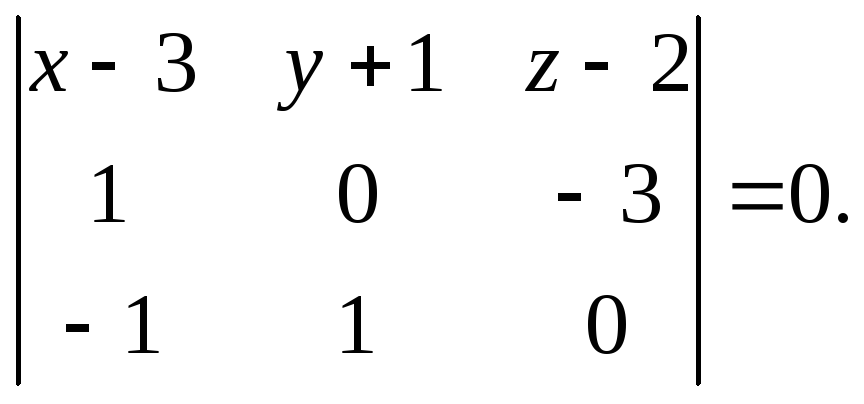
Вычисляя определитель по правилу треугольников, получим: или .

Теорема 7.1. В пространстве всякая плоскость выража-ется уравнением 1-й степени ,

Доказательство. В предыдущем пункте было установлено, что всякая плоскость может быть задана уравнением вида (12):

,

Раскрыв скобки и обозначив , получим общее уравнение 1-й степени относительно x, y, z: , эквивалентное уравнению (12). Поэтому оно определяет ту же плоскость, что и уравнение (12), и называется общим уравнением плоскости. Коэффициенты при переменных в этом уравнении сохраняют тот же геометрический смысл, что и в равенстве (12), то есть являются координатами нормального вектора плоскости. Так как нормальный вектор плоскости является ненулевым, то коэффициенты A, B и C не могут быть одновременно равны нулю. Итак, мы доказали, что всякая плоскость в определяется уравнением 1-й степени относительно переменных координат x, y, z.

Теорема 7.2 (обратная). Всякое линейное уравнение с тремя переменными определяет плоскость в пространстве , если хотя бы один из коэффициентов при переменных не равен нулю.

Доказательство. Пусть x₀, y₀, z₀ – какое-либо решение данного уравнения. Тогда , откуда . Подставляя в данное уравнение вместо D его значение и группируя члены, получим

Это уравнение плоскости, проходящей через точку и имеющей нормальный вектор Следовательно, и равносильное ему уравнение определяет плоскость, перпендикулярную вектору

Пример 7.3. Построить в прямоугольной системе ко-ординат плоскость, заданную уравнением .

Решение. Для построения плоскости необходимо и достаточ-но знать какие-либо три ее точки, не лежащие на одной прямой, нап-ример, точки пересечения плоскости с осями координат. Полагая в заданном уравнении , получим . Следовательно, за-данная плоскость пересекает ось Oz в точке Ана-логично при получим , то есть точку ; при получим , то есть точку . По трем точкам , , строим заданную плоскость (рис. 7.3).

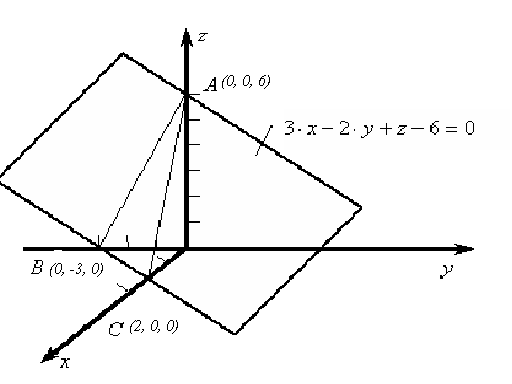
Рис. 7.3

Частные случаи общего уравнения плоскости. Рассмотрим особенности расположения плоскости в тех случаях, когда те или иные коэффициенты общего уравнения обращаются в нуль.

1. При уравнение определяет плоскость, проходящую через начало координат, так как ко-ординаты точки удовлетворяют этому уравнению.

2. При уравнение определяет плоскость, параллельную оси Ох, поскольку нормальный вектор этой плоскости перпендикулярен оси Ох (его проек-ция на ось Ох равна нулю). Аналогично при плоскость параллельна оси Оу, а при плоскость параллельна оси Оz.

3. При уравнение определяет плоскость, проходящую через ось Ох, поскольку она параллельна оси Ох () и проходит через начало координат (). Аналогично плоскость проходит через ось Оу, а плоскость – через ось Оz.

4. При уравнение определяет плоскость, параллельную координатной плоскости Оxу, поскольку она параллельна осям Oх () и Оу (). Аналогично плоскость параллельна плоскости уОz, а плоскость – плоскости Оxz.

5. При уравнение (или ) определяет координатную плоскость Оxу, так как она параллельна плоскости Оxу () и проходит через начало координат Аналогично уравнение в пространстве определяет координатную плоскость Оxz, а уравнение – координатную плоскость Оyz.

Пример 7.4. Составить уравнение плоскости P, проходящей через ось Оу и точку .

Решение. Уравнение плоскости, проходящей через ось Оу, имеет вид . Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P. Поэтому ее координаты удовлетворяют написанному выше урав-нению плоскости: Û , откуда Подставив найденное значение A в уравнение , получим: или .

Это и есть искомое уравнение.