1.F-тест качества спецификации множественной регрессионной модели.

F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера. F_факт определяется как

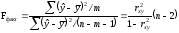
гду n — число единиц совокупности;

m - число параметров при переменных х

F_табл – это максимально возможное значение критерия под влия­нием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть пра­вильную гипотезу при условии, что она верна. Обычно а принимает­ся равной 0,05 или 0,01.

Если F_табл<F_факт, то Н₀ - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл>F_факт, то гипотеза Н₀ не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

2.Автокорреляция случайного возмущения. Причины. Последствия.

Автокорреляция случайных возмущений означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.

В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(ε_t ε_S) = 0,при t ≠ s) гарантирует некоррелированность значений случайных членов в раз­личные моменты наблюдений и это позволяет получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные моменты времени на­зывается автокорреляцией (сериальной корреляцией).

Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной объясняющей переменной); наличие неучтенных факторов; использование ошибочной функциональной зависимости, а иногда и характер наблюдений (например, временные ряды).

Для проверки на автокорреляцию используется ряд крите­риев, из которых наиболее широкое применение получил крите­рий Дарбина-Уотсона

Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяются следующие:

1. Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок

2. Дисперсии оценок являются смещенными. Зачастую дисперсии, вычисляемые по стандартным формулам, являются заниженными, что приводит к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться.

3. Оценка дисперсии регрессии 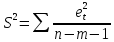является смещенной оценкой истинного значения , во многих случаях занижая его.

4. В силу вышесказанного выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

4.Автокорреляция. Методы устранения автокорреляции

Автокорреляция случайных возмущений означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.

При отрицательной автокорреляции можно видеть, что положительные значения имеют тенденцию следовать за отрицательными и наоборот.

При положительной автокорреляции положительные значения чаще следуют за положительными, а отрицательные за отрицательными.

При больших ρ процесс становится нестационарным, приближаясь к случайному блужданию. С ρ = 0.9 последовательность значений с одним знаком становится длинной, а тенденция возврата к 0 слабой.

Устранение автокорреляции.

1. В линейной регрессионной модели либо в моделях, сводящихся к линейной, наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR(1).

Модель парной регрессии: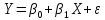 . Тогда есть два наблюдения: Тогда наблюдениям t и (1-1) соответствуют формулы

, .

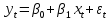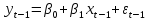Пусть случайные отклонения подвержены воздействию авторегссии первого порядка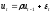

Автокорреляция AR(1) может быть устранена в лаговых моделях. Для этого нужно умножить уравнение для y_t-1 на ρ и вычесть из y_t. Случайный член 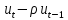(инновация) не является автокоррелированным. Проблема автокорреляции устранена.

Однако данный способ приводит к потере первого наблюдения (если мы не обладаем предшествующим ему наблюдением). Число степеней свободы уменьшится на единицу, что при больших выборках не так существенно, но при малых выборках может привести к потере эффективности. Эта проблема обычно преодолевается с помощью поправки Прайса-Уинстона:

, .

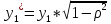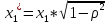Аналогично устраняется влияние автокорреляции в множественной регрессионной модели.

2. Процедура Кохрейна-Оркатта.

• По выборочным данным выполняется настройка модели и вычисляется вектор остатков регрессии e.

• По остаткам регрессии оценивается модель авторегрессии . Получаем оценку .

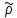• На основе этой оценки вычисляем новые оценки для y, x:

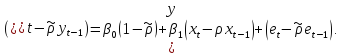
• По найденным оценкам находим регрессию _t от 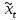и оценки 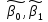. Процесс возвращается к этапу 2.

Итерационный процесс заканчивается при условии совпадения оценок на последней и предпоследней итерациях с заданной степенью точности.