57.Роль вектора и матрицы корреляции множественной линейной модели при подборе объясняющих переменных.

Объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами:

• иметь высокую вариабельность;

• быть сильно коррелированными с объясняемой переменной;

• быть слабо коррелированными между собой;

• быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих*.

Объясняющие переменные подбираются с помощью статистических методов.

Процедура подбора переменных состоит из следующих этапов:

1. На основе накопленных знаний составляется множество так называемых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную. Такие переменные будем обозначать Х1 Х2,.., Хт.

2. Собирается статистическая информация о реализациях как объясняемой переменной, так и потенциальных объясняющих переменных. Формируется вектор у наблюдаемых значений переменной Y и матрица X наблюдаемых значений переменных Х1, Х2, ..., Хт в виде

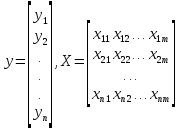
3. Исключаются потенциальные объясняющие переменные, характеризующиеся слишком низким уровнем вариабельности.

4. Рассчитываются коэффициенты корреляции между всеми рассматриваемыми переменными.

5. Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры

Вектор и матрица коэффициентов корреляции

Для оценивания силы линейной зависимости объясняемой переменной Y от потенциальных объясняющих переменных Х1, Х2, .., Хт рассчитываются коэффициенты корреляции

Эти коэффициенты представляются в виде вектора корреляции:

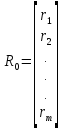
Коэффициенты корреляции между потенциальными объясняющими переменными Х1, Х2, ..., Хт рассчитываются по формуле

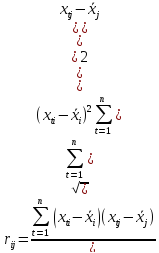
образуют матрицу корреляции R:

Матрица R симметрична, т. е. rij= rji

58.Свойства дисперсии случайной переменной

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата её отклонения от математического ожидания: D(X)=M[X-M(X)]² или D(X)=M(X-a)² где a=M(X).

(Для дисперсии СВ Х используется также обозначение Var(X).)

Дисперсия характеризует отклонение (разброс, рассеяние, вариацию) значений СВ относительно среднего значения.

Если СВ Х – дискретная с конечным числом значений, то

.

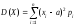Дисперсия D(X) имеет размерность квадрата СВ, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину .

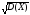Свойства дисперсии СВ:

1) D(C)=0, где C – постоянная величина;

2) D(kX)=k²D(X);

3) D(X)=M(X²)-a² где a=M(X);

4)D(X+Y)=D(X-Y)=D(X)+D(Y), где X и Y – независимые случайные величины.

59.Случайные переменные и их характеристики.

Переменная величина х с областью изменения Х называется случайной, если свои возможные значения q из множества Х переменная х принимает в результате некоторого опыта со случайными элементарными исходами вида w:х=q. Это элементарное событие означает, что переменная величина х в опыте приняла значение q.

Случайная переменная именуется дискретной случайной величиной, если множество Х состоит из конечного или счетного количества констант qi . Случайная переменная х именуется непрерывной случайной переменной, если множество Х является промежутком числовой прямой и вероятность каждого элементарного исхода равна 0.

Полной характеристикой случайной переменной х служит ее дифференциальный закон распределения. Так называется функция Px(q) скалярного аргумента q, определенная на всей числовой прямой, характеризующая объективную возможность появления в опыте значений q случайной переменной х. Если х – дискретная случайная переменная, то

Cледовательно Рх (qi) –это вероятность появления в опыте значения qi случайной переменной х. Функция именуется вероятностной функцией дискретной случайной переменной х.

Так же важную роль имеют две количественные характеристики случайной переменной х: математическое ожидание (или среднее значение) и дисперсия.

Мат.ожидание:

- Определение взвешенного среднего E(X) для ожидаемого значения X: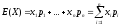

E(X) – это константа, вокруг которой рассеяны возможные значения q случайной переменной х.

Математическое ожидание функции дискретных случайных величин:

Определение E[g(X)], ожидаемого значения функции от X: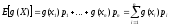

Пример:

Дисперсия и стандартное отклонение:

Дисперсия – это средний квадрат разброса возможных значений случайной переменной х относительно ее ожидаемого значения. Положительный квадратный корень из дисперсии называется средним квадратическим отклонением.

s_х² = E [(X - m)²] - дисперсия или s_х² = E(X²) - m²

s_х – стандартное отклонение