70.Теорема Гаусса – Маркова.

Пусть матрица Х уравнений наблюдений 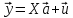имеет размер nx(k+1), где n>k+1, и обладает линейно-независимыми столбцами, а случайные возмущения(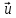 = 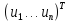) удовлетворяют четырем условиям:

E(u₁)=…=E(u_n)=0

Var(u₁)=…=Var(u_n)=

Cov(u_i,u_j)=0 , i≠j

Cov(x_mi,u_j)=0 при всех значениях m,i,j.

Тогда:

а) наилучшая линейная процедура 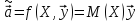имеет вид:

б) эффективная линейная несмещенная оценка обладает свойством наименьших квадратов: ESS=

в) ковариационная матрица оценки 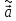вычисляется по правилу: Cov(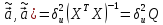

г) несмещенная оценка параметра , где n –число уравнений наблюдений, k+1 – количество неизвестных коэффициентов функции регрессии модели.

Следствие. Оценка 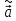, доставляемая процедурой : 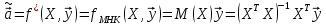метода наименьших квадратов, может быть вычислена в процессе решения системы двух линейных алгебраических уравнений:

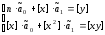именуемой системой нормальных уравнений. Ее коэф-ты и свободные члены вычисляются по правилам:

[x] = x₁ + x₂ +…+ x_n,

[y] = y₁ + y₂ +…+ y_n,

[x²] = x₁² + x₂² +…+ x_n²,

[xy] = x₁*y₁ + x₂*y₂ + … + x_n*y_n .

Вот явный вид решения системы:

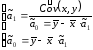
71.Тест Дарбина – Уотсона, последовательность его выполнения.

В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(ε_t ε_S) = 0,при t ≠ s) гарантирует некоррелированность значений случайных членов в раз­личные моменты наблюдений и это позволяет получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные моменты времени на­зывается автокорреляцией (сериальной корреляцией).

Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной объясняющей переменной); использование ошибочной функциональной зависимости, а иногда и характер наблюдений (например, временные ряды).

Для проверки на автокорреляцию используется ряд крите­риев, из которых наиболее широкое применение получил тест Дарбина-Уотсона.

Последовательность его выполнения:

1.оценка модели и вычисление остатков;

2. вычисление статистики DW:

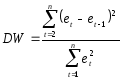
3.выбор табличных значений границ критического значения статистики: d_u, d_L ( по параметрам n, k, α);

4.определение интервала, в который попадает вычисленное значение статистики DW.

При этом возможны следующие случаи:

Наличие положительной автокорреляции: DW<d_L.

Наличие отрицательной автокорреляции: DW >4-d_L.

Автокорреляция отсутствует: d_U ≤ DW≤ 4-d_U.

Зоны неопределенности: d_L<DW< d_U или 4- d_U <DW<4-d_L.

72.Тест Стьюдента.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей.

Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т.е. определяют фактическое значение t-критерия Стьюдента

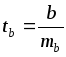где m_b – стандартная ошибка параметра ,

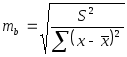где S остаточная дисперсия на одну степень свободы

Данный критерий затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2). Этот же результат можно получить после извлечения корня из F-критерия, т.е. t_b=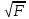. Аналогично для параметра а.

Фактическое значение t-критерия Стьюдента определяется как

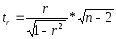
Данная формула свидетельствует о том, что в парной линейной регрессии t²_r=F. Кроме того t²_b=F, следовательно, t²_r= t²_b. Таким образом проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о значимости линейного уравнения регрессии.

Сравнивая фактическое и критическое (табличное) значения t-статистики – t_табл и t_факт - принимаем или отвергаем гипотезу H₀.

Если t_табл < t_факт, то H₀ отклоняется, т.е. a и b не случайно от­личаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t_табл > t_факт, то гипотеза Н_о не откло­няется и признается случайная природа формирования a и b.