
- •2.Автокорреляция случайного возмущения. Причины. Последствия.
- •4.Автокорреляция. Методы устранения автокорреляции
- •5.Алгоритм проверки адекватности парной регрессионной модели
- •6.Алгоритм проверки значимости регрессора в парной регрессионной модели
- •7.Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
- •8.Выбор типа математической функции при построении уравнения регрессии
- •9.Выведите формулы вычисления параметров модели парной регрессии
- •10.Гетероскедастичность - понятие, проявление и меры устранения.
- •11.Гетероскедастичность случайного возмущения. Причины. Последствия. Тест gq.
- •12.Двухшаговый метод наименьших квадратов для оценки параметров структурной формы модели
- •15.Индивидуальная и интервальная оценка индивидуального значения зависимой переменной
- •16.Интервальная оценка параметров уравнения парной регрессии
- •17.Классическая парная регрессионная модель. Спецификация модели. Теорема Гаусса – Маркова.
- •18.Ковариация, коэффициент корреляции и индекс детерминации
- •19.Количественные характеристики взаимосвязи пары случайных переменных.
- •20. Косвенный метод наименьших квадратов для оценки параметров структурной формы модели
- •21. Коэффициент корреляции и индекс детерминации в регрессионной модели.
- •22. Линейная модель множественной регрессии
- •23. Метод Монте-Карло, его применение в эконометрике
- •24. Метод наименьших квадратов: алгоритм метода; условия применения. Обобщённый метод наименьших квадратов
- •25. Модели с бинарными (фиктивными) переменными.
- •26. Моделирование тенденции временных рядов (аналитическое выравнивание)
- •27. Мультиколлинеарность факторов – понятие, проявление и меры устранения
- •28. Назначение теста Голдфелда-Квандта, этапы его проведения.
- •Нелинейная модель множественной регрессии Кобба-Дугласа. Оценка её коэффициентов.
- •30.Нелинейная регрессия (линеаризация, оценка параметров)
- •31.Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение.
- •32.Основные числовые характеристики вектора остатков в классической множественной регрессионной модели
- •33.Отражение в модели влияния неучтённых факторов и времени.
- •35.Оценка адекватности полученной эконометрической модели (см. 5)
- •36.Оценка коэффициентов модели Самуэльсона-Хикса
- •37.Оценка параметров множественной регрессионной модели методом наименьших квадратов.
- •38. Оценка параметров парной регрессионной модели методом наименьших квадратов.
- •39.Оценка параметров эконометрической модели
- •40.Оценка статистической значимости коэффициентов модели множественной регрессии. (см. 6)
- •41.Подбор объясняющих переменных множественной линейной модели. Алгоритм исключения квазинеизменных переменных
- •42.Подбор объясняющих переменных множественной линейной модели. Метод анализа матрицы коэффициентов корреляции.
- •43.Подбор переменных в модели множественной регрессии на основе метода оценки информационной ёмкости.
- •44.Понятие гомоскедастичности и гетероскедастичности случайных возмущений, их графическая интерпретация.
- •45.Порядок оценивания линейной модели множественной регрессии методом наименьших квадратов (мнк) в Excel
- •46.Последствия гетероскедастичности. Тест Голдфелда-Квандта.
- •47.Предпосылки метода наименьших квадратов
- •48.Применение обобщенного метода наименьших квадратов (омнк) для случая гетероскедастичности остатков.
- •49.Применение теста Стьюдента в процедуре подбора переменных в модели множественной регрессии.
- •50.Применение фиктивных переменных при исследовании сезонных колебаний: спецификация модели, экономический смысл параметров при фиктивных переменных.
- •52.Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности.
- •53.Проверка качества эконометрической модели См.5
- •54.Прогнозирование экономических переменных. Проверка адекватности модели. См.5
- •56.Регрессионные модели с фиктивными переменными.
- •57.Роль вектора и матрицы корреляции множественной линейной модели при подборе объясняющих переменных.
- •58.Свойства дисперсии случайной переменной
- •59.Случайные переменные и их характеристики.
- •60.Смысл и значение множественной регрессии в эконометрических исследованиях. Выбор формы уравнения множественной регрессии.
- •62.Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам
- •64.Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.
- •65.Статистические свойства оценок параметров парной регрессионной модели.
- •66.Статистические характеристики выборки и генеральной совокупности статистических данных. Их соотношения.
- •67.Суть метода наименьших квадратов. Его графическое пояснение
- •68.Схема Гаусса – Маркова.
- •69.Схема построения эконометрической модели.
- •70.Теорема Гаусса – Маркова.
- •71.Тест Дарбина – Уотсона, последовательность его выполнения.
- •72.Тест Стьюдента.
- •73. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей.
- •74. Устранение автокорреляции в парной регрессии. (см. 4)
- •75. Функция регрессии как оптимальный прогноз.
- •76. Цели и задачи эконометрики. Этапы процесса эконометрического моделирования. Классификация эконометрических моделей.
- •77. Эконометрика, её задача и метод.
- •78. Эконометрическая инвестиционная модель Самуэльсона-Хикса.
- •80. Этапы исследования зависимостей между экономическими явлениями при помощи эконометрической модели. Принципы спецификации модели. Формы эконометрических моделей.
- •81. Этапы построения эконометрических моделей
64.Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.
Одним
из основных способов корректировки
гетероскедастичности является
использование метода взвешенных
наименьших квадратов. Он применяется
в том случае, когда известны диагональные
элементы автоковариационной матрицы
 вектора возмущений
вектора возмущений
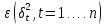 .
В этом случае уравнения наблюдений
можно преобразовать следующим образом.
Поделим каждый член на СКО возмущения:
.
В этом случае уравнения наблюдений
можно преобразовать следующим образом.
Поделим каждый член на СКО возмущения:
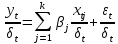 ,
где t=1….n.
В результате преобразования спецификация
принимает вид спецификации классической
регрессионной модели:
,
где t=1….n.
В результате преобразования спецификация
принимает вид спецификации классической
регрессионной модели:
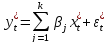 . Определим количественные характеристики
случайного возмущения
. Определим количественные характеристики
случайного возмущения
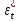 :
:
математическое
ожидание: E{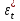 }=E{
}=E{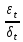 }=
}=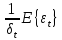 =0
=0
дисперсия
случайного члена: Var
{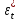 }=Var{
}=Var{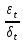 }=
}=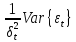 =
=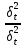 =1,
таким образом
=1,
таким образом
 ~N(0,1)
и при помощи данного преобразования
случайное возмущение приобрело свойство
гомоскедастичности.
~N(0,1)
и при помощи данного преобразования
случайное возмущение приобрело свойство
гомоскедастичности.
В
случае, если значения
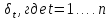 неизвестны, используется доступный
обобщенный метод наименьших квадратов.
В этом методе выполняется оценка
неизвестных дисперсий, но при условии,
что на структуру автоковариационной
матрицы накладываются дополнительные
ограничения (предпосылки). Наиболее
часто используется следующая предпосылка:
СКО возмущения пропорционально одному
из регрессоров.
неизвестны, используется доступный
обобщенный метод наименьших квадратов.
В этом методе выполняется оценка
неизвестных дисперсий, но при условии,
что на структуру автоковариационной
матрицы накладываются дополнительные
ограничения (предпосылки). Наиболее
часто используется следующая предпосылка:
СКО возмущения пропорционально одному
из регрессоров.
65.Статистические свойства оценок параметров парной регрессионной модели.
Теорема
Гаусса-Маркова. Пусть матрица Х имеет
полный ранг. При выполнении условий
Гаусса-Маркова МНК-оценки параметров
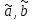 относятся к классу линейных по Y,
несмещенных оценок с минимальной
дисперсией. Покажем линейность оценок
следующим выражением:
относятся к классу линейных по Y,
несмещенных оценок с минимальной
дисперсией. Покажем линейность оценок
следующим выражением:
 Докажем несмещенность полученных
оценок. Введем обозначение:
Докажем несмещенность полученных
оценок. Введем обозначение: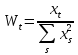 , тогда можно показать, что справедливы
следующие соотношения:
, тогда можно показать, что справедливы
следующие соотношения:
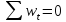 ,
,
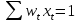 ,
,
 ,
,
 .
Свойство несмещенности оценок параметра
проверяется соответственно:
.
Свойство несмещенности оценок параметра
проверяется соответственно:
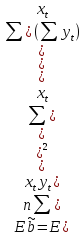 ,
,
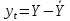 ,
E(
,
E( )=b
)=b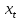 ,
E
,
E =a.
Оценка является состоятельной если:
=a.
Оценка является состоятельной если:
 ,
т.е с увеличением объема выборки оценки
более плотно концентрируются около
истинного значения. Оценка становится
более надежной в вероятностном смысле,
и дисперсия оценки стремится к нулю.
Для доказательства состоятельности
оценок параметров парной регрессии
получим выражения для элементов
автоковариационной матрицы вектора
оценок параметров
,
т.е с увеличением объема выборки оценки
более плотно концентрируются около
истинного значения. Оценка становится
более надежной в вероятностном смысле,
и дисперсия оценки стремится к нулю.
Для доказательства состоятельности
оценок параметров парной регрессии
получим выражения для элементов
автоковариационной матрицы вектора
оценок параметров
 .
В матричной форме
.
В матричной форме
 =AY,
поэтому
=AY,
поэтому
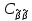 =Cov{AY,AY}=
=Cov{AY,AY}=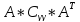 .
Определим элементы автоковариационной
матрицы случайного вектора Y:
.
Определим элементы автоковариационной
матрицы случайного вектора Y:
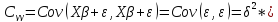
 ,
где
,
где
 -единичная
матрица с размером nxn.
Таким образом
-единичная
матрица с размером nxn.
Таким образом
 =
=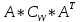 =(
=(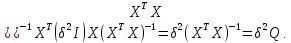 Так как Q=
Так как Q=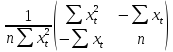 ,
получим выражения элементов ковариационной
матрицы вектора
,
получим выражения элементов ковариационной
матрицы вектора
 через выборочные данные:
через выборочные данные:
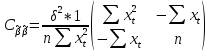 ,
таким образом имеем:
,
таким образом имеем:
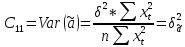 ,
,
 .
Как следует из этих выражений, с
увеличением объема выборки n
дисперсии несмещенных оценок параметров
стремятся к нулю, то есть МНК-оценки
параметров парной регрессии являются
состоятельными.
.
Как следует из этих выражений, с
увеличением объема выборки n
дисперсии несмещенных оценок параметров
стремятся к нулю, то есть МНК-оценки
параметров парной регрессии являются
состоятельными.
В
качестве эффективности оценок чаще
всего используется критерий вида:
Е{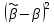 }=
}=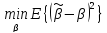 .
Несмещенная оценка является эффективной,
если она имеет минимальную дисперсию
по сравнению с любыми другими оценками
этого параметра в классе выбранных
процедур(т.е. является менее случайной).
Доказательство эффективности МНК-оценок
.
Несмещенная оценка является эффективной,
если она имеет минимальную дисперсию
по сравнению с любыми другими оценками
этого параметра в классе выбранных
процедур(т.е. является менее случайной).
Доказательство эффективности МНК-оценок
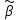 выполняется
путем сравнения их дисперсий с дисперсиями
линейных несмещенных оценок
выполняется
путем сравнения их дисперсий с дисперсиями
линейных несмещенных оценок
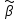 .
Пусть
.
Пусть
 -вектор
несмещенных линейных оценок параметров
-вектор
несмещенных линейных оценок параметров
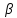 ,
определяемых выражением вида
,
определяемых выражением вида
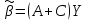 ,
где С- произвольная(2хn)-
матрица. Тогда в силу несмещенности
оценки
,
где С- произвольная(2хn)-
матрица. Тогда в силу несмещенности
оценки
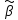 и равенства AX=
и равенства AX=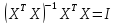 ,
можно записать:
,
можно записать:
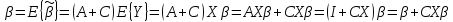 ,
откуда следует, что CX=0.
Определим автоковариационную матрицу
,
откуда следует, что CX=0.
Определим автоковариационную матрицу
 вектора оценок
вектора оценок
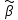 :
:
 ,
так как Cov{Y,Y}=
,
так как Cov{Y,Y}=
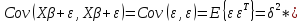 I и С
I и С =0,
A
=0,
A =
=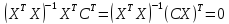 .
Диагональные элементы автоковариационной
матрицы-дисперсии оценок параметров.
Диагональные элементы
.
Диагональные элементы автоковариационной
матрицы-дисперсии оценок параметров.
Диагональные элементы
 неотрицательны, поэтому Var(
неотрицательны, поэтому Var( Var(
Var(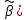 ,
т.е МНК-оценка
,
т.е МНК-оценка
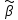 является эффективной, имея минимальную
дисперсию по сравнению с любыми
несмещенными оценками неизвестного
параметра в классе линейных процедур
является эффективной, имея минимальную
дисперсию по сравнению с любыми
несмещенными оценками неизвестного
параметра в классе линейных процедур
