20. Экономический смысл 3 теоремы двойственности

Третья теорема двойственности позволяет определить зависимость изменения целевой функции начальной задачи от изменения запасов "ресурсов"

Теорема .(об оценках). Двойственные оценки пока­зывают приращение функции цели, вызванное малым из­менением свободного члена соответствующего ограниче­ния задачи математического программирования, точнее

15. Симплекс метод с искусственным базисом

Применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи ЛП, записанной в канонической форме.

М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной ЗЛП таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М – достаточно большое положительное число.

В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки Д у теперь будут зависеть от «буквы М». Для сравнения оценок нужно помнить, что М– достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.

В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.

Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.

Исходная ЗЛП имеет решение, если в оптимальном плане расширенной ЗЛП все искусственные переменные равны нулю.

18.Задача рационального использования ресурсов. Экономический смысл ограничений двойственных задач, их переменных и их оптимальных решений

Для изготовления 2 видов продукции ()используются ресурсы 3 видов (). Запасы ресурсов на предприятии, расход запасов каждого вида на единицу продукции каждого вида, прибыль от реализации продукции представлены в таблице.

			Запасы
	12	4	300
	4	4	120
	3	12	252
Прибыль	30	40

Необходимо составить план производства продукции обеспечивающего макс прибыль:

-объем пр-ва по плану, -объем пр-ва

-ограничение по (расход), - по,-по

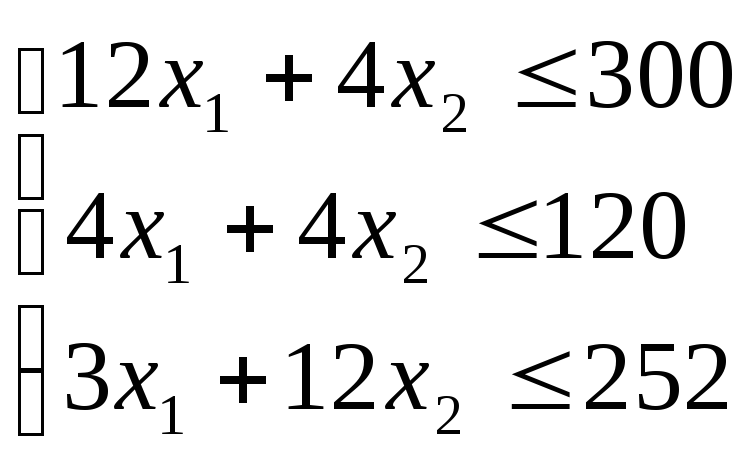
Двойственная задача:

Пусть уi – оценки ресурсов i-вида (внутр. цены, учетные цены, теневые, ненастоящие, объективно обусловленные оценки ресурсов)

F(x) = 300y1 + 120y2 + 252y3

Пряма задача полягає у визначенні такого оптимального плану виробництва продукції, який дає найбільший дохід. Економічний зміст двоїстої задачі полягає ось у чому. Визначити таку оптимальну систему двоїстих оцінок ресурсів у_і, використовуваних для виробництва продукції, для якої загальна вартість усіх ресурсів буде найменшою. Оскільки змінні двоїстої задачі означають цінність одиниці і-го ресурсу, їх інколи ще називають тіньовою ціною відповідного ресурсу. За допомогою двоїстих оцінок можна визначити статус кожного ресурсу прямої задачі та рентабельність продукції, що виготовляється. Якщо двоїста оцінка уі в оптимальному плані дорівнює нулю, то відповідний і-й ресурс є недефіцитним. Якщо ж двоїста оцінка є більшою за нуль, то відповідний ресурс є дефіцитним.

Ліва частина кожного обмеження двоїстої задачі є вартістю всіх ресурсів, які використовуються для виробництва одиниці j-ї продукції. Якщо ця величина перевищує ціну одиниці продукції, то дана продукції є нерентабельної, виготовляти її невигідно. Якщо ж вона дорівнює ціні, то вона є рентабельною. В оптимал. плані прямої задачі їй відповідна змінна x_j0.