8.Свойства задач линейного программирования.

Общая задача линейного программирования в канонической форме состоит в нахождении вектора X=(X₁,X₂,..,X_n), обеспечивающего наибольшее (наименьшее) значение линейной формы:

(1) при условиях: (2) (3)

План называется опорным , если он обращает в равенство хотя бы n независимых ограничений (2)-(3).

Опорный план, содержащий ровно m положительных компонент, называется невырожденным , и в противном случае - вырожденным (здесь m - число независимых ограничений в (2)).

Множество планов называется выпуклым, если всякая точка множества лежит на отрезке, соединяющем какие-нибудь две точки множества.

Точка называется граничной, если любая сколь угодно малая окрестность этой точки содержит как точки данного монжества, так и точки, не принадлежащие ему.

Точка наз. внутренней для множества, если существует окрестность этой точки, содержащая только точки данного множества.

Множество планов называют замкнутым, если его граница принадлежит этому множеству.

Точка X множества назывего вершиной или крайней точкой, если ее нельзя поместить внутри отрезка, соединяющего какие-то две точки множества.

Выпуклое замкнутое множество с конечным числом вершин называется выпуклым многогранником.

Теоремы:

1. Любая точка многогранника явл. выпуклой линейной комбинацией его угловых точек

2. Пересечение любого числа выпуклых множеств – выпуклое множество

3. ОДР ЗЛП – выпуклое множество

4. Если в ЗЛП имеется оптимальное решение, то целевая функция принимает его в одной из угловых точек. Если более чем в одной, то оптимальным решением является любая точка, являющаяся их выпуклой линейной комбинацией (оптим. решение – на границе)

5. Каждому допустимому базисному решению задач линейного программирования соответствует угловая точка.

Вывод: если ЗЛП имеет оптимальное решение, то его нужно искать в одной из угловых точек многогранника-решения

16.Симметричные двойственные задачи

Разновидностью двойственных задач линейного программирования являются двойственные симметричные задачи, в ко­торых система ограничений как исходной, так и двойственной задач задается неравенствами, причем на двойст­венные переменные налагается условие неотрицательности.

Исходная	Двойственная
, , i=1,m	, , j=1,n
, , i=1,m	, , j=1,n

Исходная задача. Найти минимальное значение линейной функции Z = x1 + 2x2 + 3x3 при ограничениях

xi 0 (i=1,2,3)

Очевидно, для того чтобы записать двойственную задачу, сначала необходимо систему ограничений исходной задачи привести к виду (1.12). Для этого второе неравенство следует умножить на -1.

Двойственная задача. Найти максимум линейной функции f = 2y1+ 3y2 + 6y3 + 3y4 при ограничениях

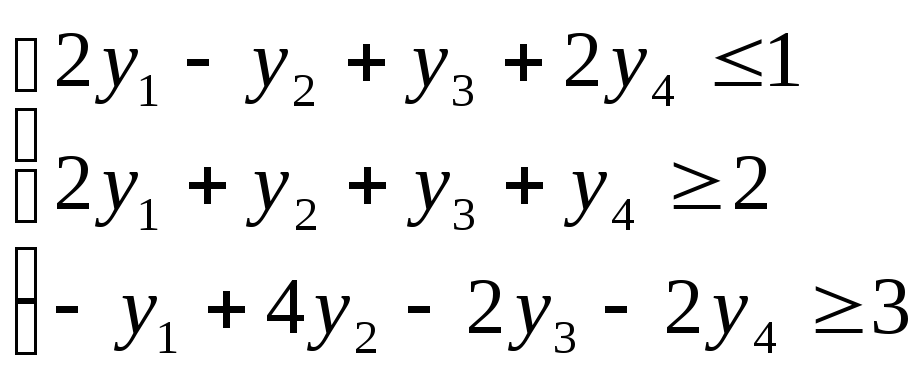
Для решения исходной задачи необходимо ввести четыре дополни­тельные переменные и после преобразования системы - одну искус­ственную. Таким образом, исходная симплексная таблица будет состо­ять из шести строк и девяти столбцов, элементы которых подлежат преобразованию.

Для решения двойственной задачи необходимо ввести три допол­нительные переменные. Система ограничений не требует предваритель­ных преобразований, ее первая симплексная таблица содержит четыре строки и восемь столбцов.

Используя симметричность, можно выбрать задачу, более удобную для решения. Объем задачи, решаемой с помощью ЭВМ, ограничен числом включаемых строк, поэтому задача, довольно громоздкая в исходной постановке, может быть упрощена в двойственной формулировке. При вычислениях без помощи машин использование двойственности упрощает вычисления.