29. Определение границ утойчивости двоственных оценок

Величина двойственной оценки того или иного ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу. Двойственные оценки измеряют эффективность малых приращений объемов ресурсов в конкретных условиях данной задачи. Если целью является расширение производства и повышение эффективности плана путем привлечения дополнительных ресурсов, то анализ оценок поможет выбрать правильное решение. Прирост различных ресурсов будет давать неодинаковый эффект, т.е. оценки позволяют с большей точностью выявить узкие места, сдерживающие рост эффективности производства. С учетом всех конкретных условий задачи оценки показываю, какие ресурсы более дефицитны, какие менее дефицитны и какие избыточны.

Как известно, область устойчивости двойственных оценок - это область изменения свободных членов ограничений, при которой двойственные оценки не меняются. Неизменность двойственных оценок говорит о том, что не меняют своих номеров базисные и свободные переменные в решении.

25. Транспортная задача по критерию времени

В рассматриваемой задаче критерием качества организации перевозок являются не суммарные затраты, а время реализации перевозок (подобные проблемы возникают при транспортировке скоропортящихся грузов, при переброске сил быстрого реагирования и т.д.).

Пусть имеется m поставщиков продукта в количествах A_i (i=1.. m) и n потребителей в количествах B_j (j = 1 .. n), причем соблюдается баланс предложения и спроса.

Известно время t_ij доставки груза от i - го поставщика к j - му потребителю, не зависящее от объема перевозки.

Требуется среди всех допустимых планов перевозок X = {X_ij} найти план, оптимальный по времени. Очевидно, что время, необходимое для реализации плана, совпадает с наибольшим временем отдельных перевозок и оптимальное время перевозок равно

при условиях

X_ij  0, i = 1 .. m, j = 1 .. n

Алгоритм решения базируется на идеях венгерского метода для классической транспортной задачи и элементарном здравом смысле.

Предварительно выбирается минимальное значение t_ij и строится допустимая сеть по значениям t_ij, не превышающим выбранного.

В этой сети отыскивается максимальный поток. Если этот поток отвечает условиям задачи, то выбранное время оптимально. В противном случае выбирается очередное наименьшее время, сеть расширяется и в ней вновь ищется максимальный поток.

Очевидно, что для выбора начального времени разумнее отталкиваться не от минимального значения, а от максимального среди минимальных времен в строках и столбцах матрицы

26. Задача о назначениях

Одной из специальных оптимизационных задач, сводящихся к задачам линейного целочисленного программирования является задача о назначениях, с помощью которой можно получить ответ на вопросы типа: как распределить рабочих по станкам, чтобы общая выработка была наибольшей или затраты на заработную плату наименьшими; как наилучшим образом распределить экипажи самолетов; как назначить людей на различные должности (отсюда и название задачи) и т.д.

Математически такие задачи относятся к типу распределительных задач, с той особенностью, что в них объемы наличных и требующихся ресурсов для выполнения каждой работы равны единице (ai = bj = 1), а все переменные хij либо равны единице, если i-й работник назначен на j-ю работу, либо равны нулю в других случаях. Исходные данные задачи о назначениях группируются в таблице, которая называется матрицей оценок, а результаты – в матрице назначений.

Задача о назначениях в общем виде может быть сформулирована следующим образом. Имеется n работников, которые могут выполнять n работ, причем использование i-ro работника на j-й работе, например, приносит доход Сij. Требуется поручить каждому из работников выполнение одной вполне определенной работы, чтобы максимизировать в данном случае суммарный доход.

Введем переменные:

Задача состоит в том, чтобы найти распределение

работников по работам (т. е. найти матрицу назначений), которое максимизирует целевую функцию

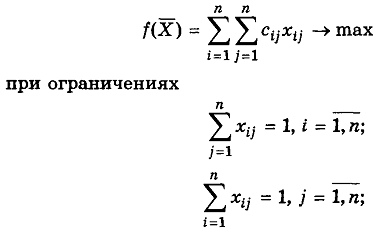Оптимальные экономико-математические модели причем равно либо 0, либо 1 (так называемые булевы переменные) для всех

Ограничения отражают условие того, что за каждым работником может быть закреплена только одна работа, а ограничения (3.25) означают, что для выполнения каждой работы может быть выделен только один работник.

Если в задаче о назначениях элементы матрицы оценок представляют собой, например, время выполнения каждым работником любой из работ, то целевая функция этой задачи будет минимизироваться. Следует заметить также, что при решении задачи о назначениях часто используются алгоритмы и методы решения транспортных задач, в частности, метод потенциалов.