33. Метод гомори

Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи без учета целочисленности переменных. Если среди компонент нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования. Если же в оптимальном плане переменная x_j принимает дробное значение, то к системе уравнений добавляют неравенство

и находят решение задачи.

В неравенстве a_ij* и b_i*- преобразованные исходные величины a_ij и b_i, значения которых взяты из последней симплекс-таблицы, а f(a_ij*) и f(b_i*) - дробные части чисел (под дробной частью некоторого числа a понимается наименьшее неотрицательное число b такое, что разность между a и b есть целое). Если в оптимальном плане задачи дробные значения принимают несколько переменных, то дополнительное неравенство определяется наибольшей дробной частью.

Если в найденном плане задачи, переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычисления повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования, либо устанавливают ее неразрешимость.

Из изложенного выше следует, что процесс определения оптимального плана задачи целочисленного программирования методом Гомори включает следующие основные этапы:

1. Используя симплексный метод, находят решение задачи без учета требования целочисленности переменных.

2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи имеет максимальное дробное значение, а в оптимальном плане задачи должна быть целочисленной.

3. Используя двойственный симплекс–метод, находят решение задачи, получающейся из задачи в результате присоединения дополнительного ограничения.

4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи или установления ее неразрешимости.

47. Сведение матричных игр к злп

Рассмотрим игру mxn определяемую матрицей

Согласно теореме 3, для оптимальной стратегии первого игрока U*=(u1*, u2*, …, um*) и цены игры v выполняется неравенство

Предположим для определенности, что v>0. Это всегда может быть достигнуто благодаря тому, что прибавление ко всем элементам матрицы A одного и того же постоянного числа C не приводит к изменению оптимальных стратегий, а только лишь увеличивает цену игры на C.

Разделив теперь обе части последнего неравенства на v, получим

Положим ui*/v=yi*, тогда

Так как первый игрок стремиться получить максимальный выигрыш, то он должен обеспечить минимум величине 1/v. С учетом этого, определение оптимальной стратегии первого игрока сводится к нахождению минимального значения функции

Аналогичные рассуждения показывают, что определение оптимальной стратегии второго игрока сводится к нахождению максимального значения функции

Здесь xj=zj/v. Таким образом, чтобы найти решение данной игры, определяемой матицей A, нужно составить следующую пару двойственных задач и найти их решение.

Прямая задача: Двойственная задача:

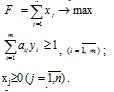
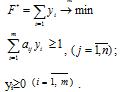
Используя решение пары двойственных задач, получаем формулы для определения стратегий и игры: