2. Примеры экономических задач.

Задача о рациональном использовании ресурсов

Для изготовления 2 видов продукции()используются ресурсы 3 видов (). Запасы ресурсов на предприятии, расход запасов каждого вида на единицу продукции каждого вида, прибыль от реализации продукции представлены в таблице.

			Запасы
	12	4	300
	4	4	120
	3	12	252
Прибыль	30	40

Необходимо составить план производства продукции обеспечивающего макс прибыль:

-объем пр-ва по плану, -объем пр-ва

-ограничение по (расход),- по,-по

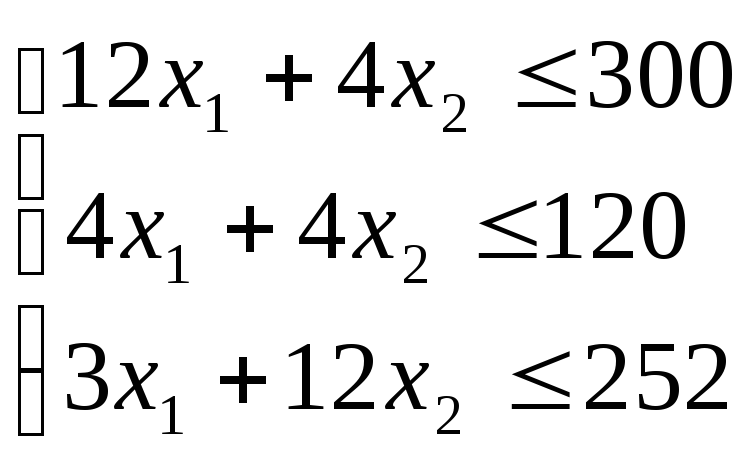
Задача о составлении рациона

Имеется 2 вида кормов ( и ), содержащих 4 вида питательных веществ (,, , ). Необходимый минимум данных пит веществ в ежедневном рационе, стоимость единицы нормы каждого вида, а также содержания кол-ва единиц пит. веществ соответствующего вида в единице корма соответствующего вида в единице корма соответствующего типа указаны в таблице:

			Необх миниум
	3	1	6
	1	4	2
	1	1	5
	6	1	10
Стоимость единицы корма, грн	2	3

- кол-во единиц в смеси, - кол-во единиц .

, ,

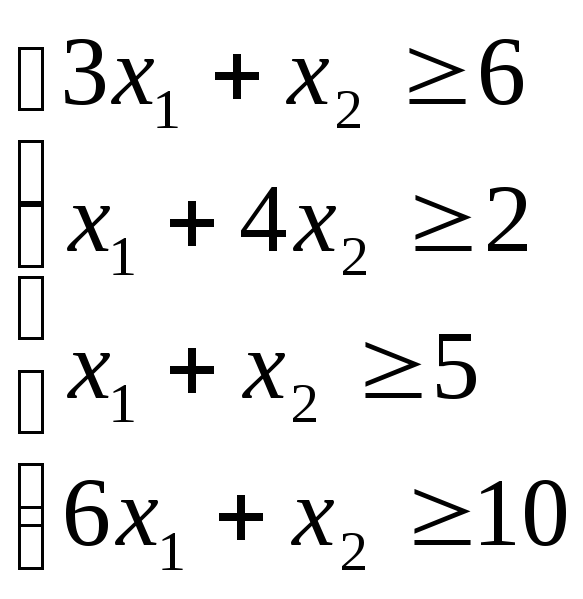
4.Этапы решения экономических задач математическими методами.

1.)формируется предмет и цель исследования ; 2.)выделяются структурные и функциональные элементы, выявляются наиболее важные качественные характеристики; 3.)словесно описываются взаимосвязи между элементами модели; 4.)водятся символические обозначения: -переменные(), к-ые полностью характеризуют данный процесс; -составляется система ограничений, к-ой удовлетворяют данные переменные и к-ая следует из ограниченности запасов ресурсов и неотрицательности переменных; -задается целевая функция, критерий эффективности; 5.)проводятся расчеты по мат модели и анализируются полученные решения с использованием ПК.

5.Принципы построения экономико-математических моделей.

-необходимо соизмерять точность и потребность мат модели с: 1. точностью тех данных, к-ми располагает исследователь; 2.теми результатами, к-ые необходимо получить;

-мат модель должна отражать существующие черты объекта и при этом не должна его сильно упрощать; -так как матмодель не может быть полностью адекватной исследуемому процессу явления, то для изучения данного экономического объекта рекомендуется несколько моделей, затем полученные результаты сравнивают. Если они сходные , исследование заканчивают, а если сильно отличаются то требуется пересмотреть постановку задачи;

-любая сложная система(комплекс взаимосвязанных элементов вместе с отношениями между элементов и их свойствами) всегда подвержена внешним и внутренним воздействиям, следовательно, матмодель должна быть устойчивой, т.е. сохранять свои свойства и структуру при этих воздействиях.