Часть 3. Расчет системы автоматического управления

с И – регулятором и с П – регулятором для объекта,

не обладающего запаздыванием в канале регулирования

Этап 1. Анализ динамических свойств объекта,

не обладающего запаздыванием в канале регулирования,

во временной и частотной областях

Анализ динамических свойств объекта управления во временной и частотной областях по каналу регулирования и по трем каналам возмущения выполнен в первом этапе второй части пояснительной записки.

Этап 2. Синтез замкнутой САУ с И - регулятором и с П – регулятором

на заданную степень колебательности m=0,221

для объекта без запаздывания в канале регулирования

2.1 Расширенные частотные характеристики объекта управления по каналу регулирования

Синтез замкнутой САУ осуществляется методом расширенных частотных характеристик. Для определения расширенных частотных характеристик объекта по каналу регулирования необходимо в передаточной функции объекта сделать подстановку: p=-m·+j·, где m=0.221заданная степень колебательности системы. Передаточная функция по каналу регулирования имеет вид:

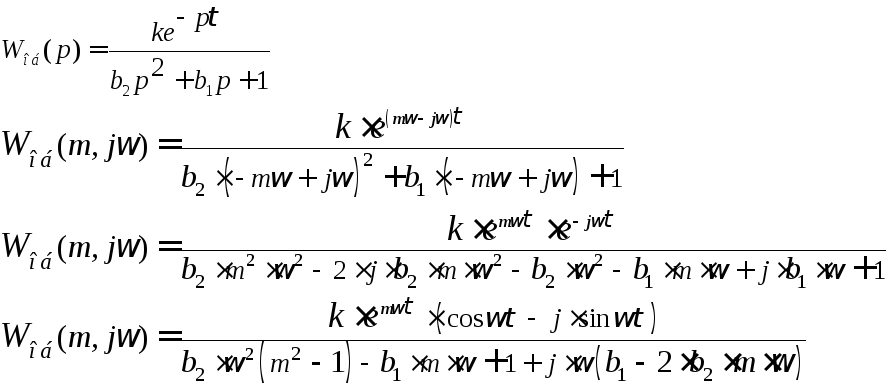
- расширенная амплитудно-частотная характеристика объекта по каналу регулирования

Выражение для расширенной амплитудно-частотной характеристики найдем как отношение модулей числителя и знаменателя:

Расширенная АЧХ проходит выше обыкновенной АЧХ.

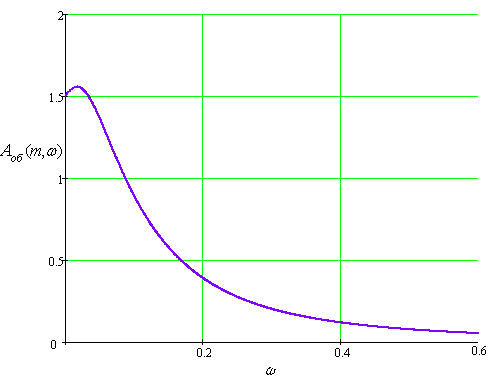
Расчетные данные для построения РАЧХ в Таблице 45.

Таблица 45

	0	0,005	0,01	0,03	0,04	0,05	0,1	0,2	0,3	0,5	1
A(m,)	1,5	1,529	1,548	1,523	1,456	1368	0,895	0,392	0,203	0,078	0,02

Рис.63 Расширенная амплитудно-частотная характеристика по каналу регулирования со степенью колебательности m=0,221 и без запаздывания.

- расширенная фазо-частотная характеристика объекта по каналу регулирования

Выражение для расширенной фазо-частотной характеристики найдем как разность аргументов числителя и знаменателя:

Функция имеет две точки разрыва, в которых функция arctg изменяется с/2 до -/2, однако нас интересует поведение функции при положительном значении частоты ω. Чтобы найти эти точки, необходимо приравнять знаменатель функциик нулю.

Для обеспечения непрерывности графика РАФХ необходимо прибавить период, равный -:

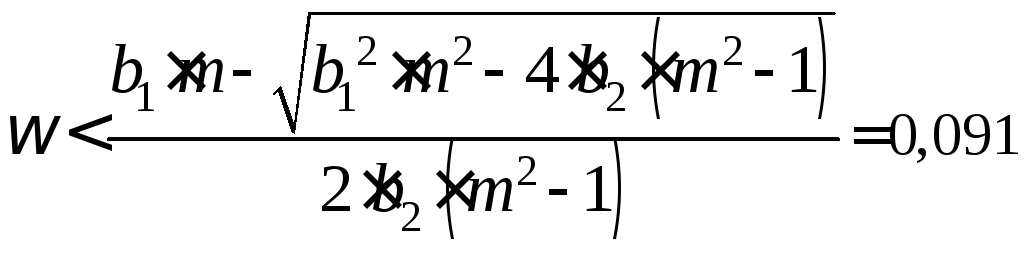
при

при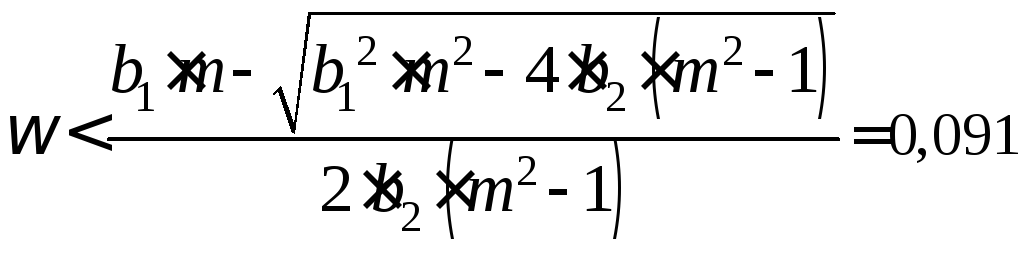

Расчетные данные для построения РФЧХ в Таблице 46. Расширенная ФЧХ проходит ниже обыкновенной ФЧХ.

Таблица 46

	0	0,005	0,01	0,03	0,07	0,1	0,3	0,7	1	3
(m,)	0	-0,101	-0,204	-0,617	-1,302	-2,083	-2,721	-3,202	-3,316	-3,491

Рис.64 Расширенная фазо-частотная характеристика по каналу регулирования со степенью колебательности m=0,221 и без запаздывания.

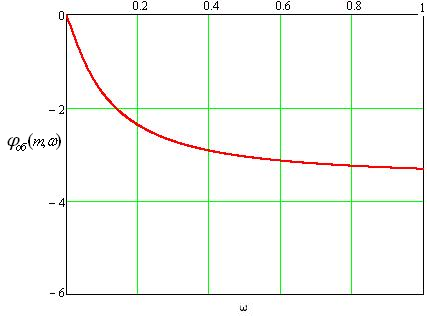
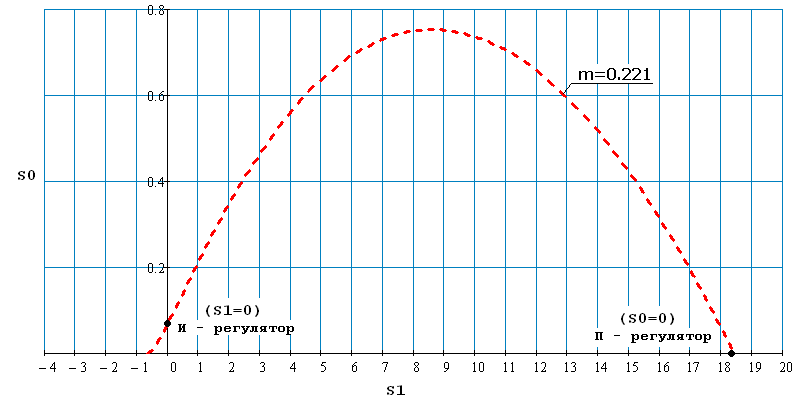
2. Построение кривой равной степени колебательности m=0,221 для объекта без запаздывания и выбор оптимальных настроечных параметров И - регулятора и П – регулятора.

Для реализации задачи синтеза САУ необходимо в плоскости настроек И – регулятора и в плоскости настроек П – регулятора построить кривую равной степени колебательности и на ней выбрать точку, соответствующую минимуму квадратичной интегральной оценки качества. Эта точка обычно находится при _опт= 1.3^._max, где_max– значение частотыв максимуме графикаS₀(S₁).

Чтобы заданная система имела переходный процесс с заданной степенью колебательности mнужно, чтобы РАФХ заданной системы проходила через точку с координатами (-1,j^·0), т.е.:

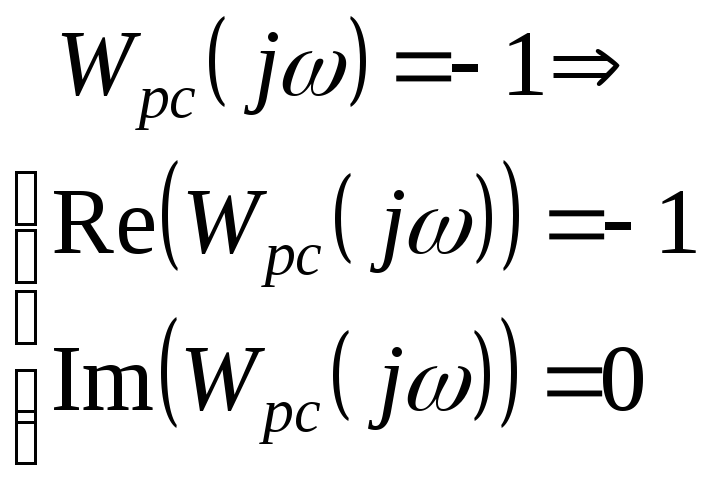
При этом степень колебательности будет равна m. Из этих условий найдем настройки пропорционально-интегрального регулятораДля этого в передаточной функции регулятора сделаем подстановку: p=-m·+j·,:

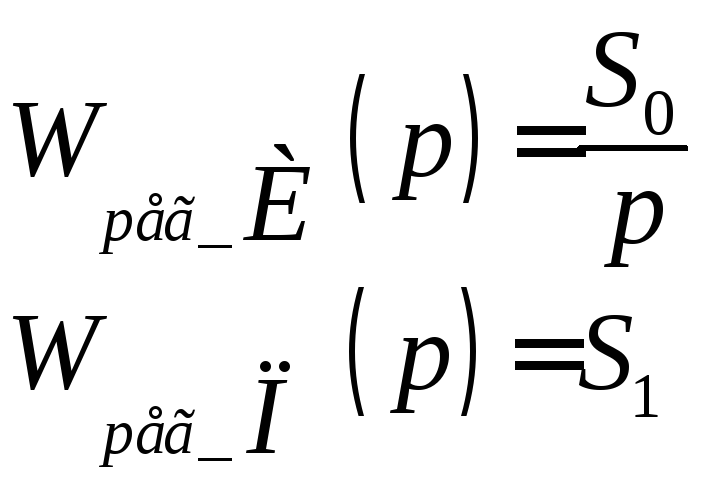
Представим передаточную функцию объекта в показательном виде:

Используя уравнение Эйлера, получим:

Поскольку передаточную функцию разомкнутой системы можно представить в виде произведения передаточных функций объекта и регулятора , следовательно, передаточную функцию разомкнутой системы можно также представить в показательном виде. В свою очередь, условия устойчивости по критерию Найквиста представим в показательной форме, то есть мы можем составить систему из двух уравнений:

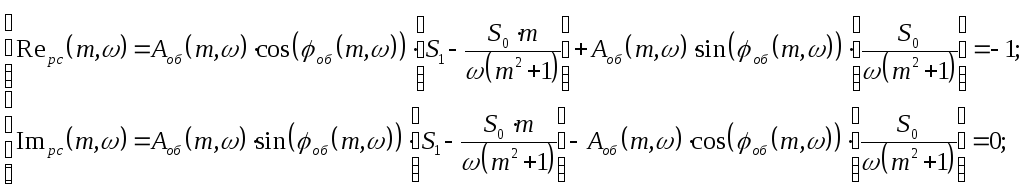
Можно получить область, где находятся значения настроечных параметров S₀,S₁,.

Решая систему уравнений, найдем настройки интегрального регулятора

и пропорционального регулятора.

Настройки И – регулятора:

Настройки П – регулятора:

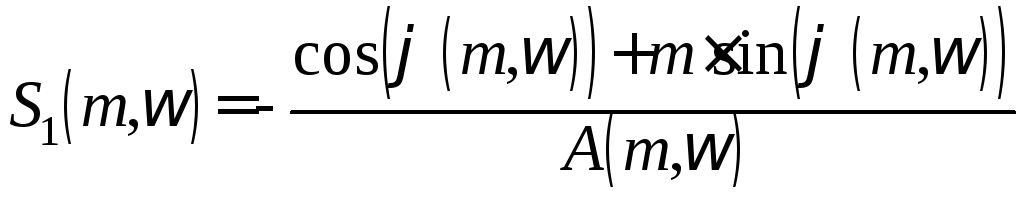
Используя полученные уравнения настроек И – регулятора и П - регулятора, и задавая различные значениям , получим кривую заданной степени колебательностиm=0,221.

Расчетные данные для построения кривой равной степени колебательности с И – регулятором и с П – регулятором в Таблице 47

Таблица 47

	0	0,03	0,05	0,1	0,2	0,39829	0,45	0,51777	0,55	0,6
S1	-0,667	-0,451	-0,265	0,349	2,219	8,45	10,627	13,825	15,484	18,232
S0	0	0,012	0,032	0,117	0,374	0,754	0,72	0,532	0,374	0,028

Оптимальные настройки для И – регулятора S0_опт=S0(m,_опт) = 0,067

Оптимальные настройки для П – регулятора S1_опт=S1(m,_опт) = 18,421

Рис.65 Кривая равной степени колебательности m=0,221, без запаздывания с И – регулятором и с П – регулятором.