2.4. Адекватность. Критерий Дарбина – Уотсона

Проверка адекватности трендовых моделей реальному процессу строится на основе анализа случайной компоненты. В расчетах случайная компонента заменяется остатками, представляющими собой разность фактических и расчетных значений

(2.28)

Принято считать, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам случайности, независимости и подчиняются нормальному закону распределения.

При правильном выборе тренда отклонения от него будут носить случайный характер. В случае если вид функции выбран неудачно, то последовательные значения остатков могут не обладать свойством независимости, т.е. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок.

Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является критерий Дарбина – Уотсона. Этот критерий связан с гипотезой о существовании автокорреляции первого порядка. Его значения определяются по формуле

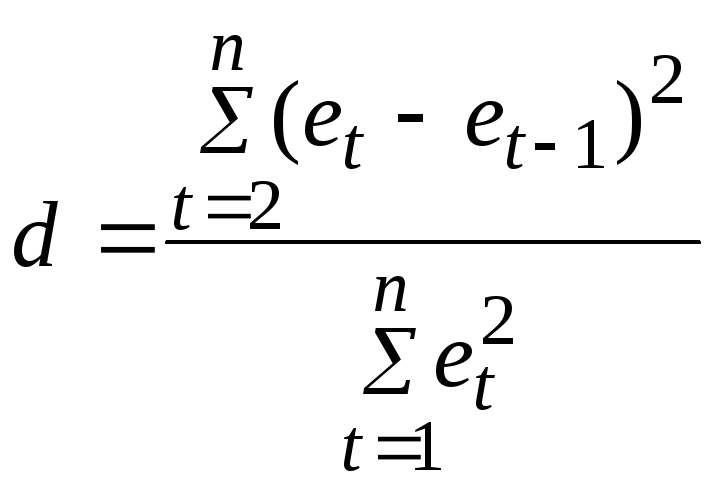. (2.29)

Для понимания смысла этой формулы преобразуем ее, сделав предварительное допущение, положив . Непосредственное преобразование формулы осуществляется следующим образом:

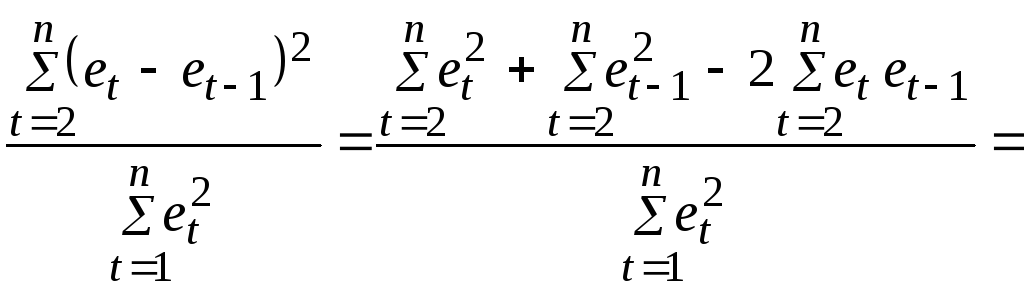
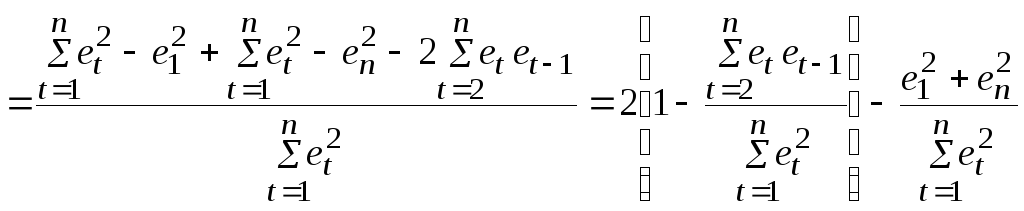При достаточно большом сумма из слагаемых значительно превосходит сумму из двух слагаемых и поэтому отношением этих величин можно пренебречь. Кроме того, отношение в квадратных скобках в силу того, что , можно считать коэффициентном корреляции между и . Таким образом, критерий Дарбина – Уотсона записывается в виде

. (2.30)

Полученное представление критерия позволяет сделать вывод, что статистика Дарбина – Уотсона связывает с выборочным коэффициентом корреляции . Таким образом, , и значение критерия может указывать на наличие или отсутствие автокорреляции в остатках. Причем, если , то . Если (положительная автокорреляция), то ; если (отрицательная автокорреляция), то .

Статистически значимая уверенность в наличии или отсутствии автокорреляции определяется с помощью таблицы критических точек распределения Дарбина – Уотсона. Таблица позволяет по заданному уровню значимости , числу наблюдений и количеству переменных в модели определить два значения: – нижняя граница и – верхняя граница.