
- •В.В. Давнис, в.И. Тинякова эконометрические методы прогнозирования
- •1. Теоретические основы прогнозирования
- •1.1. Сущность экономического прогнозирования
- •1.2. Типология прогнозов
- •1.3. Этапы прогнозирования
- •2. Экстраполяция временных рядов
- •2.1. Сущность экстраполяции
- •2.2. Типы роста и трендовые модели
- •2.3. Метод наименьших квадратов (мнк)
- •В общем случае поиск оптимальных параметров сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай
- •Решая линейную систему (2.26) с помощью замены
- •2.4. Адекватность. Критерий Дарбина – Уотсона
- •2.5. Критерии точности прогнозных расчетов
- •3. Регрессионный анализ и прогноз
- •3.1. Множественная регрессия
- •3.1.1. Основные понятия регрессионного анализа
- •3.1.2. Общий вид модели множественной регрессии
- •3.1.3. Метод наименьших квадратов в матричной форме
- •3.1.4. Парная регрессия как частный случай множественной
- •3.1.5. Мультиколлинеарность факторов
- •3.1.6. Особенности применение регрессионных моделей в прогнозных расчетах
- •3.2. Обобщенный регрессионный анализ
- •3.2.1. Обобщенная схема мнк
- •Здесь использован тот факт, что
- •3.2.2. Метод взвешенных наименьших квадратов
- •3.2.3. Корректировка стандартных ошибок
- •3.2.4. Тесты на гетероскедастичность
- •3.3. Регрессионные модели с автокоррелированными остатками
- •3.3.1.Общая схема мнк в случае автокорреляции первого порядка
- •3.3.2. Методы тестирования на автокорреляцию
- •3.3.3. Методы оценивания параметра
- •3.3.4. Прогнозные расчеты при автокоррелированных остатках
- •3.4. Регрессионные модели с лаговыми переменными
- •3.4.1. Общий вид моделей с лагами в независимых переменных
- •4. Авторегрессионные процессы и их модели
- •4.1. Стационарность
- •4.2. Модель авторегрессии
- •4.3. Понятие интеграции
- •4.4. Модели скользящей средней
- •4.5. Авторегрессионные модели скользящей средней
- •4.6. Авторегрессионные интегрированные модели скользящей средней
- •4.7. Коэффициент автокорреляции и проверка его значимости
- •4.8. Определение порядка моделей arma
- •4.9. Построение моделей arima
- •4.10. Проверка адекватности моделей arma
- •4.11. Оценка точности прогнозных расчетов по моделям arima
- •5. Адаптивные модели прогнозирования
- •5.1. Специфика адаптивного моделирования
- •5.2. Полиномиальные модели
- •5.3. Рекуррентный метод наименьших квадратов
- •5.4. Многофакторные адаптивные модели
- •5.5. Адаптивные многошаговые модели
- •5.6. Выбор начальных значений и
- •6. Прогнозирование сезонных колебаний
- •6.1. Моделирование периодических колебаний
- •Эта запись получена с использованием тригонометрического тождества
- •6.2. Аддитивная и мультипликативная модели
- •6.3. Моделирование сезонных колебаний
- •6.4. Адаптивные модели сезонных явлений
5.3. Рекуррентный метод наименьших квадратов
Прежде чем рассмотреть адаптивные многофакторные модели, приведем схемы рекуррентного метода наименьших квадратов (РМНК), лежащих в основе построения этих моделей. Благодаря совместному использованию рекуррентной схемы оценивания и процедуры экспоненциального сглаживания удается построить прогнозные модели, в которых, по сути, реализованы основные принципы адаптации.
Изложим сначала одношаговую схему РМНК. Для этого введем следующие обозначения:
n – объем выборочной совокупности;
![]() –
число независимых
переменных моделей;
–
число независимых
переменных моделей;
![]() –
–
![]() -я
вектор-строка
независимых переменных;
-я
вектор-строка
независимых переменных;
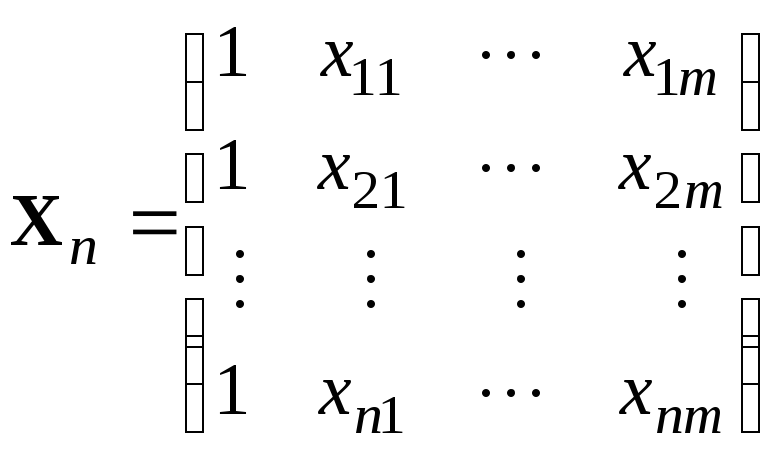 –(
n
x
(m+1))-матрица
из независимых переменных.
–(
n
x
(m+1))-матрица
из независимых переменных.
Чтобы понять, как формируется матрица системы нормальных уравнений, запишем выражение для произведения вектора-столбца на вектор-строку
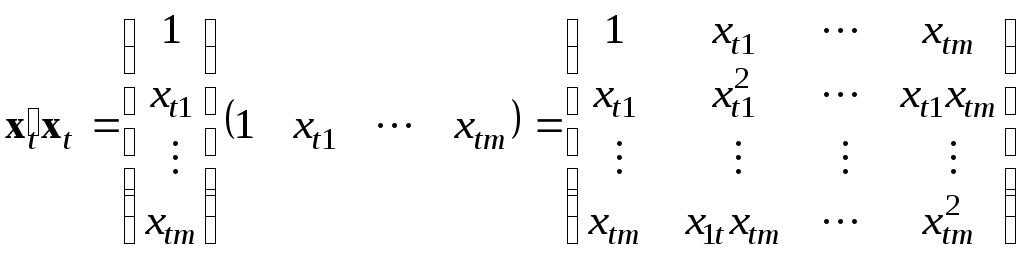 .
.
Используя данное представление, можно записать схему вычисления матрицы системы нормальных уравнений следующим образом:
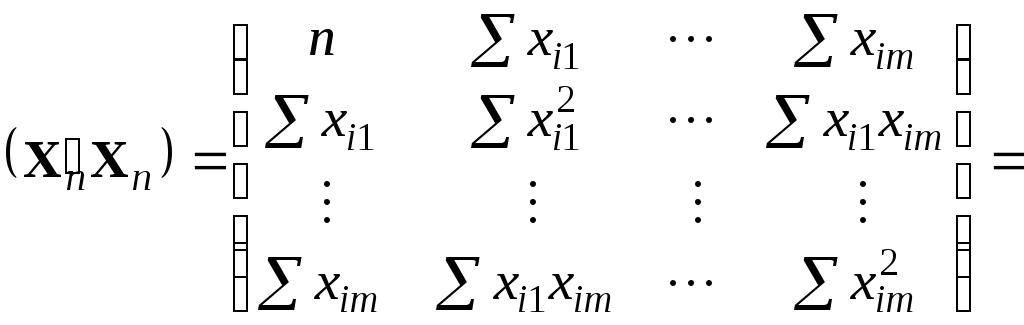
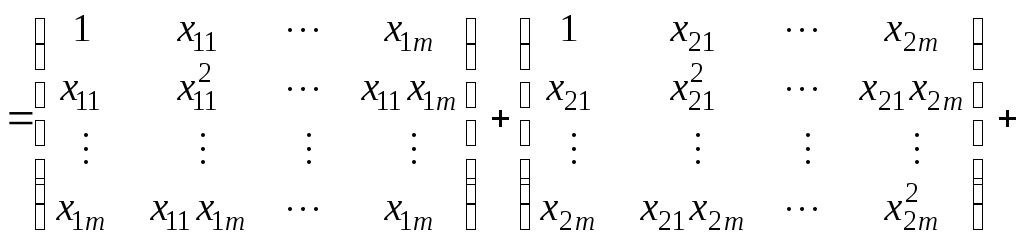
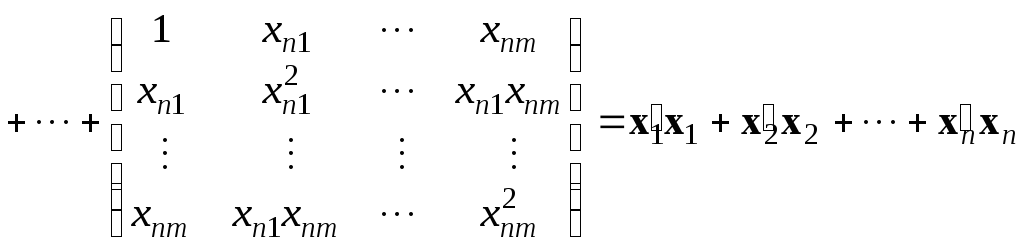 .
.
Такая схема
формирования матрицы
![]() делает понятным запись
делает понятным запись
![]() .
.
Аналогично можно записать
![]() ,
,
где
![]() –
вектор-столбец из n
зависимых переменных.
–
вектор-столбец из n
зависимых переменных.
Рассмотрим линейную регрессионную модель
![]() ,
(5.33)
,
(5.33)
где
![]() – вектор-столбец коэффициентов модели,
– вектор-столбец коэффициентов модели,
![]() –
вектор-столбец
ненаблюдаемых случайных составляющих.
–
вектор-столбец
ненаблюдаемых случайных составляющих.
Предположим, что
уже получены оценки ее коэффициентов
![]() по
данным выборочной совокупности из (
по
данным выборочной совокупности из (![]() )
наблюдения. Требуется в ситуации, когда
в выборочную совокупность добавлено
новое наблюдение
)
наблюдения. Требуется в ситуации, когда
в выборочную совокупность добавлено
новое наблюдение
![]() ,
пересчитать оценки коэффициентов
регрессии, используя для этого ранее
полученные оценки
,
пересчитать оценки коэффициентов
регрессии, используя для этого ранее
полученные оценки
![]() .
Такие ситуации возникают при обработке
очень больших массивов данных, когда
их хранение вызывает определенные
затруднения, а также, как уже отмечалось,
в тех случаях, когда по смыслу решаемой
задачи требуется последовательная
обработка вновь поступающих наблюдений.
.
Такие ситуации возникают при обработке
очень больших массивов данных, когда
их хранение вызывает определенные
затруднения, а также, как уже отмечалось,
в тех случаях, когда по смыслу решаемой
задачи требуется последовательная
обработка вновь поступающих наблюдений.
В рассматриваемой ситуации формулу для вычисления вектора оценок коэффициентов регрессионной модели можно записать следующим образом:
![]()
![]() .
(5.34)
.
(5.34)
Для удобства обозначим
![]() .
.
Далее будем использовать формулу Шермана – Моррисона для рекуррентного обращения матриц
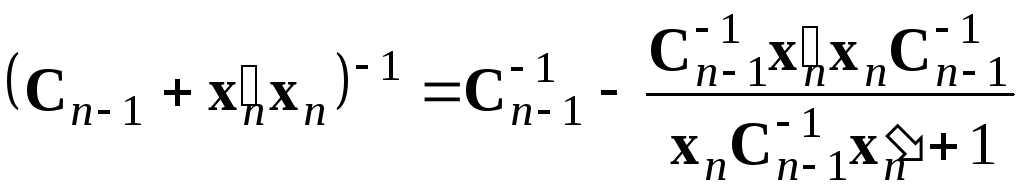 .
(5.35)
.
(5.35)
Используя формулу (5.35), выражение (5.34) можно переписать в виде
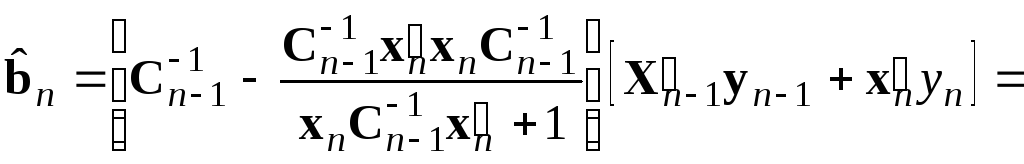
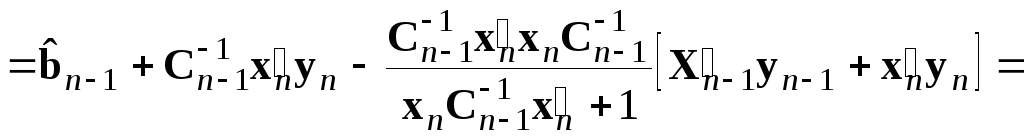
Перегруппируем члены полученного выражения
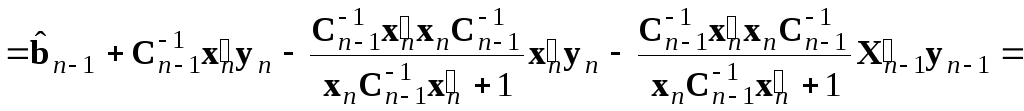
Объединив второй
и третий члены и вынеся общие множители
![]() и
и
![]() ,
а также, выполнив умножение в последнем
члене выражения, получаем
,
а также, выполнив умножение в последнем
члене выражения, получаем
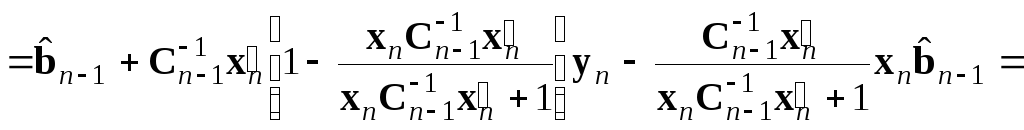
Окончательно, выполнив приведение к общему знаменателю в квадратных скобках, получаем
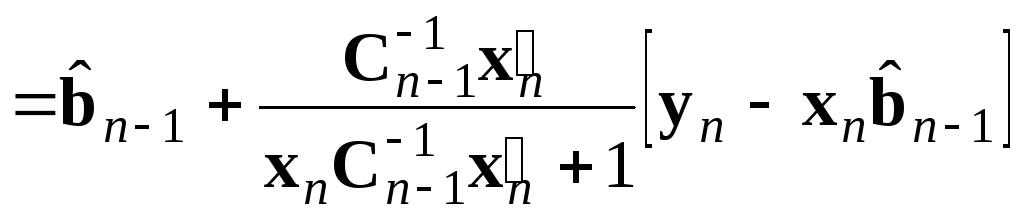 .
(5.36)
.
(5.36)
Полученная формула позволяет осуществлять пересчет оценок рекуррентно по мере появления новых наблюдений. С ее помощью реализуются основные идеи построения адаптивных многофакторных регрессионных моделей.
Перейдем к изложению схемы многошагового РМНК. Применение многошаговой процедуры возникает в тех ситуациях, когда выборочная совокупность пополняется одновременно несколькими наблюдениями. В принципе эти наблюдения можно обработать последовательно с помощью рассмотренной выше одношагового РМНК. Однако не всегда такой подход удобен. Кроме того, при настройке параметров адаптивной модели в некоторых случаях возникает необходимость учитывать информацию, полученную в результате нескольких одновременно проведенных измерений. Поэтому имеет смысл обратиться к многошаговой процедуре.
Введем дополнительные обозначения:
![]() –
матрица из
k
последних строк независимых переменных
выборочной совокупности;
–
матрица из
k
последних строк независимых переменных
выборочной совокупности;
![]() –
вектор-столбец,
компонентами которого являются k
последних наблюдений зависимой
переменной;
–
вектор-столбец,
компонентами которого являются k
последних наблюдений зависимой
переменной;
![]() – (k
x
k)-единичная
матрица.
– (k
x
k)-единичная
матрица.
Используя прием, аналогичный рассмотренному выше, запишем формулу для расчета вектора оценок коэффициентов регрессионной модели следующим образом:
![]()
![]() .
(5.37)
.
(5.37)
Для удобства обозначим
![]() .
.
Используя формулу Шермана – Моррисона – Вутбери
![]() ,
(5.38)
,
(5.38)
перепишем выражение (5.37), заменив в нем обратную матрицу на (5.38), и проведем ряд очевидных преобразований полученного выражения
![]()
![]()
![]()
![]()
![]()
Результат перемножения в третьем члене взаимоуничтожается со вторым членом, а вынесение общего множителя из четвертого и пятого членов приводит к рекуррентной форме
![]() .
(5.39)
.
(5.39)
С помощью полученной формулы осуществляется рекуррентный пересчет оценок в тех случаях, когда новые наблюдения появляются не по одному, а целыми группами сразу.
