2.1.1. Прямая как пересечение двух неколлинеарных плоскостей

Рассмотрим две плоскости A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0. Пусть векторы – нормали этих плоскостей не коллинеарны, их координаты не пропорциональны, а значит не выполняется хотя бы одно из равенств

.

Отсюда следует, что хотя бы один из трех определителей

(13)

отличен от нуля. Тогда данные плоскости пересекаются по прямой, уравнение которой имеет вид (такое уравнение прямой называют общим)

, (14)

где хотя бы один из определителей (13) не равен нулю. Заметим, что направляющий вектор прямой (14) ортогонален каждому из векторов и

,

откуда следует, что .

Поставим задачу: перейти от уравнения прямой (14) к её каноническому уравнению. Чтобы написать каноническое уравнение прямой, необходимо знать какую-нибудь точку на прямой и её направляющий вектор . Что касается направляющего вектора, то этим вектором может служить векторное произведение [,].

.

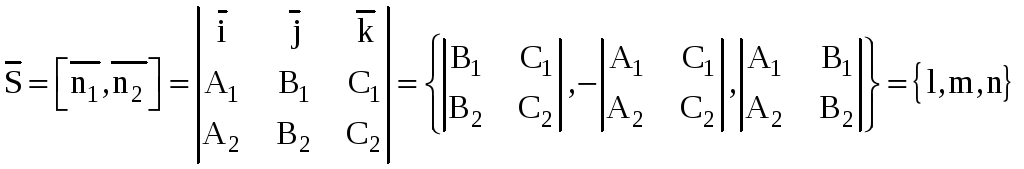Чтобы определить какую-нибудь точку М₀(x₀,y₀,z₀) на прямой, следует выбрать одно частное решение из множества решений системы (14). Для этого достаточно применить одну из координат точки М₀ равной нулю, так, если

,

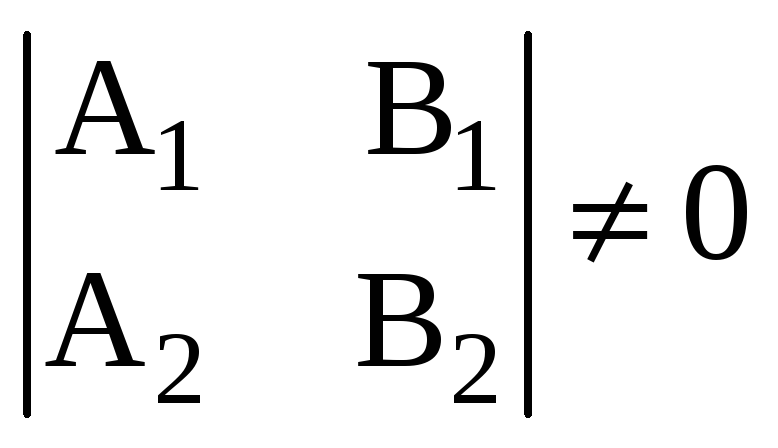то полагаем z₀=0 и находим единственное решение системы

.

2.1.2. Угол между двумя прямыми

По определению углом между двумя прямыми называют угол между их направляющими векторами. Пусть заданы канонические уравнения двух прямых:

и

.

Тогда острый угол φ между прямыми L₁ и L₂ определяется равенством:

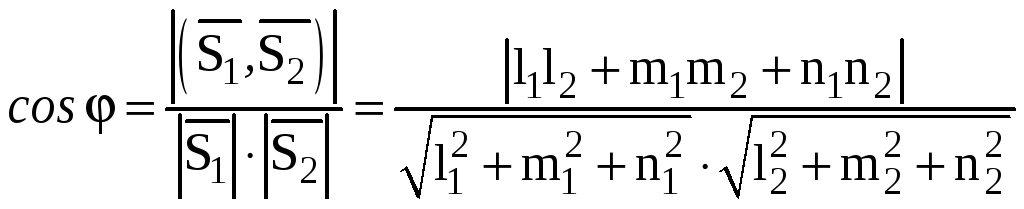. (15)

Отсюда, условие перпендикулярности прямых L₁ и L₂ имеет вид:

. (16)

Параллельность двух прямых означает коллинеарность их направляющих векторов. Тогда условие параллельности двух прямых:

. (17)

2.2. Прямая и плоскость в пространстве

Пусть в пространстве заданы прямая L

и плоскость π: Ax+By+Cz+D=0.

Взаимное расположение прямой L и плоскости π сводится к трем случаям:

а) прямая L параллельна плоскости π (не пересекает её);

б) прямая L пересекает плоскость под углом φ;

в) прямая L лежит на плоскости π.

Опишем эти случаи подробнее.

Острый угол φ между прямой L и плоскостью π определяется по формуле

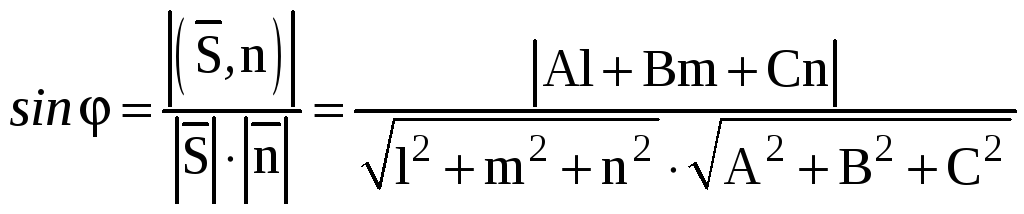. (17)

Условие параллельности прямой и плоскости π эквивалентно условию ортогональности направляющего вектора и вектора нормали , т.е.

(,)=0 . (18)

Условие перпендикулярности прямой L и плоскости π сводится к условию коллинеарности векторов =(l,m,n) и

. (19)

Частным случаем параллельности прямой и плоскости является случай (С) – прямая L принадлежит плоскости π. В этом случае, кроме условия (18) должно выполняться условие принадлежности любой точки прямой плоскости π. В частности, точка М₀, принадлежащая L, лежит на плоскости π и удовлетворяет её уравнению

Ax₀+By₀+Cz₀+D=0. (20)

Итак, условия (18) и (20) задают условия принадлежности прямой плоскости .

Решим теперь задачу отыскания координат точки пересечения прямой и плоскости. Рассмотрим эту задачу на конкретном примере.

Найти точку пересечения прямой

и плоскости 3x + 5y – z – 2 = 0.

1. Запишем параметрические уравнения прямой:

x = 4t + 12; y = 3t + 9; z = t + 1,

здесь t = .

Мы знаем, что каждой точке М прямой, соответствует своё значение параметра t.

2. Найдём значение параметра t для общей точки прямой и плоскости. Потребуем, чтобы точка М(x(t), y(t), z(t)) удовлетворяла уравнению плоскости:

3(4t + 12) + 5(3t + 9) – (t +1) – 2 = 0;

26t = – 78, t = – 3.

3. Найденное значение параметра t подставим в выражения для координат точки. Получим координаты точки пересечения прямой и плоскости

x = 0, y = 0, z = – 2.