1.2.2. Общее уравнение плоскости. Неполное уравнение
Раскрывая скобки и обозначая свободный член – Ax0 – By0 – Cz0 = D, получим общее уравнение плоскости в пространстве R3:
Ax+By+Cz+D=0, A2+B2+C2>0. (4)
Итак, линейное
относительно текущих координат x,y,z
уравнение (4) определяет плоскость в
пространстве (причем,
=(A,B,C)
ее нормаль). Можно показать, что верно
и обратное утверждение: всякое линейное
уравнение (4) в пространстве R3
определяет некоторую плоскость.
Пример. Написать уравнения координатных плоскостей.
Для того, чтобы написать уравнение любой плоскости надо знать координаты какой-нибудь точки на плоскости и какой-нибудь вектор, перпендикулярный плоскости.
В нашем примере все координатные плоскости проходят через точку M0(0,0,0) – начало координат.
А в качестве
нормалей к координатным плоскостям
можно взять соответственно базисные
векторы
.
Плоскость XOY:
М0(0,0,0),
(0,0,1)=(A,B,C).
0(x – 0) + 0(y – 0) + 1(z – 0)=0
Уравнение плоскости XOY: z=0.
Плоскость YOZ:
M0(0,0,0),
:
Уравнение плоскости YOZ: x=0.
Плоскость XOZ:
M0(0,0,0),
:
Уравнение плоскости XOZ: y=0.
Заметим, что в нашем примере в уравнениях координатных плоскостей отсутствуют два члена с текущими координатами (какие-либо два из коэффициентов A,B,C равны нулю).
Уравнение плоскости
(4), в котором хотя бы один из коэффициентов
A,B,C
или D равен нулю, называют
неполным уравнением плоскости. В
этих случаях плоскость либо параллельна
одной из координатных осей (один из
коэффициентов A,B,C
равен нулю, или, что то же, вектор нормали
ортогонален одной из координатных
осей); либо плоскость (4) параллельна
одной из координатных плоскостей (два
из коэффициентов A,B,C
равны нулю,
параллелен какой-нибудь координатной
оси); если же коэффициент D
уравнения (4) равен нулю, т.е. точка (0,0,0)
удовлетворяет уравнению плоскости,
плоскость проходит через начало
координат.
1.2.3. Уравнение плоскости «в отрезках»
Если мы имеем полное уравнение плоскости (4) и ни один из коэффициентов A,B,C,D не равен нулю, то плоскость (4) пересекает оси координат, и можно найти координаты точек пересечения.
Уравнение Ax + By + Cz + D = 0 запишем в виде
Ax + By + Cz = – D
,
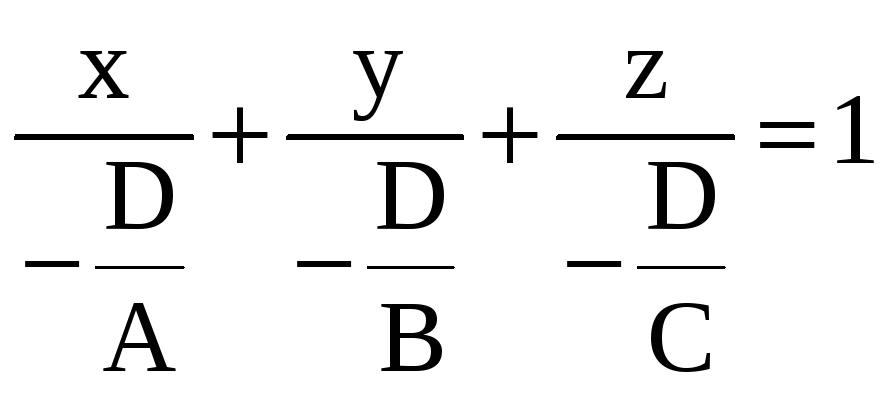обозначив а= –
,
b= –
,
c= –
,
получим уравнение плоскости «в отрезках»
.
(5)
Легко проверить, что точки M1(a,0,0), M2(0,b,0) и M3(0,0,c), лежащие на координатных осях, удовлетворяют уравнению (5) (рис. 3).
z 
с
М3
b
М2 y
а
М1
x
Рис. 3
Точки М1,М2,М3 лежат на трех плоскостях – двух координатных и плоскости (4) и могут быть найдены как решение системы трех линейных уравнений:
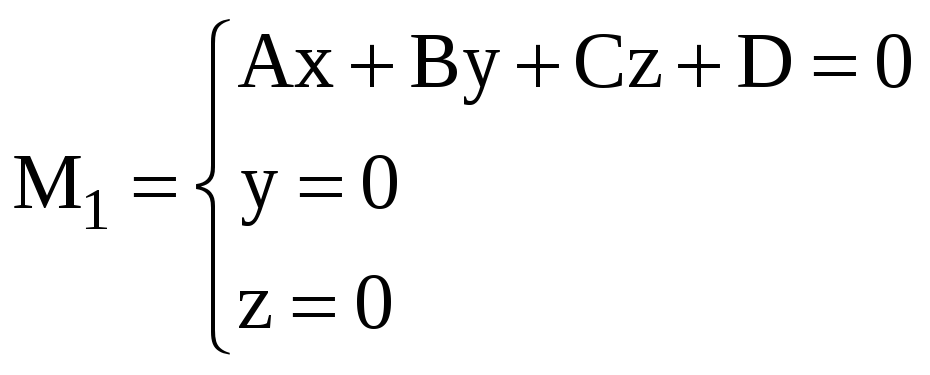т.
;
т.
;
т.
.
И вообще, если три плоскости пересекаются в одной точке, то координаты этой точки можно найти, решив систему из трех уравнений (например, по правилу Крамера). Заметим, что две не параллельные плоскости пересекаются по прямой линии, а система двух уравнений имеет бесчисленное множество решений.