1.1.2. Векторное произведение

Определение. Векторное произведение двух векторов и – это вектор , обозначаемый =[,] или =, такой что:

1) ;

2) и , т.е. векторное произведение перпендикулярно плоскости векторов и ;

3) ,, образуют правую тройку.

Координаты векторного произведения [,] через координаты сомножителей =(x₁, y₁, z₁) и =(x₂, y₂, z₂) вычисляют так:

,

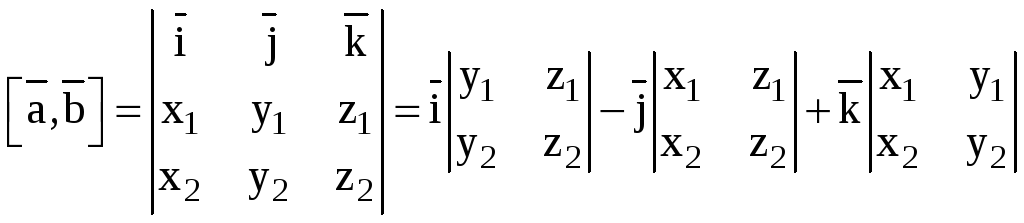т.е. координатами [,] служат определители

.

Заметим, что численно равен площади параллелограмма, построенного на векторах и (следует из определения).

Отметим также, что

.

1.1.3. Смешанное произведение

Определение. Смешанным произведением трех векторов , и называется число, обозначаемое :

=([,],)=(,[,])

Геометрический смысл смешанного произведения: если V – объем параллелепипеда, построенного на векторах , и , (рис. 1) то

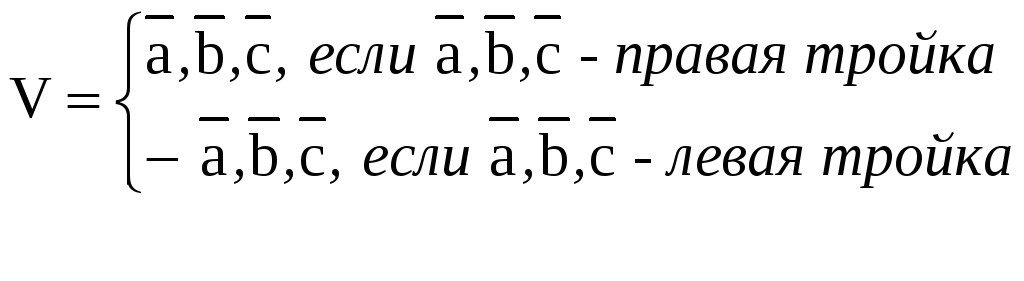
Рис. 1

Смешанное произведение в координатной форме вычисляют так:

,

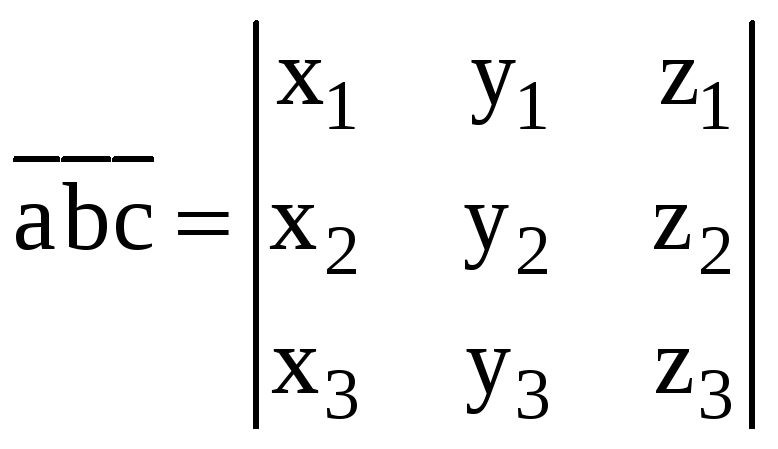где =(x₁,y₁,z₁), =(x₂,y₂,z₂) и =(x₃,y₃,z₃).

Из геометрического смысла следует условие компланарности трех векторов:

=0 ,, компланарны (лежат или параллельны одной плоскости).

1.2. Плоскость в пространстве

Пусть в пространстве R³ введена прямоугольная система координат OXYZ. Рассмотрим в пространстве некоторую поверхность Q. Поверхности Q соответствует некоторое уравнение F(x,y,z)=0, где левая часть содержит переменные x,y,z. Поверхность, определяемая уравнением F(x,y,z)=0, есть геометрическое место точек в пространстве R³, координаты которых x, y, z удовлетворяют этому уравнению. Это означает, что данному уравнению удовлетворяют координаты x, y и z каждой точки, лежащей на поверхности Q, и не удовлетворяют координаты никакой точки, не лежащей на ней. Уравнение

F(x,y,z)=0 (1)

называется уравнением данной поверхности Q. Входящие в это уравнение координаты x,y,z произвольной точки M поверхности называются текущими координатами, а сама произвольная точка М(x,y,z) поверхности Q – текущей точкой.

1.2.1. Уравнение плоскости, проходящей через точку M₀ (x₀,y₀,z₀) с данным вектором нормали =(A,B,C),

Перейдем теперь к выводу уравнения плоскости в пространстве. Геометрически плоскость однозначно можно определить различными способами. Например, тремя точками плоскости, не лежащими на одной прямой; парой параллельных прямых и др. Здесь мы рассмотрим плоскость π, проходящую через фиксированную точку M₀(x₀,y₀,z₀) и перпендикулярную вектору =(A,B,C), который называется нормалью к плоскости π, причем , т.е. A²+B²+C²>0 (рис 2).

Вектором нормали к плоскости Ax+By+Cz+D=0 называется ненулевой вектор =(A,B,C), перпендикулярный к данной плоскости.

М₀(x₀,y₀,z₀)

М(x,y,z)

Рис. 2

Пусть M(x,y,z) – текущая точка плоскости (произвольная точка плоскости π). В этом случае вектор лежит на плоскости π и, следовательно, . Воспользуемся условием ортогональности двух векторов

(,)=0 (2)

Распишем уравнение (2) покоординатно:

=(x – x₀, y – y₀, z – z₀), =(A,B,C), отсюда

A(x – x₀) + B(y – y₀) + C (z – z₀)=0 (3)

Уравнение (3) есть уравнение плоскости, проходящей через точку M₀ с вектором нормали .