3.3. Линейчатые поверхности

Среди поверхностей второго порядка различают линейчатые поверхности, т.е. поверхности, через каждую точку которых проходит прямая, целиком принадлежащая этой поверхности. К таким поверхностям, очевидно, относятся конусы и цилиндры. Но оказывается, что кроме конусов и цилиндров линейчатыми поверхностями второго порядка являются еще однополостный гиперболоид и гиперболический параболоид. Этот факт «на взгляд» не очевиден, однако легко доказывается алгебраически. Приведем доказательство для однополостного гиперболоида.

Представим каноническое уравнение однополостного гиперболоида

в виде

, или .

Рассмотрим теперь два уравнения первой степени

,

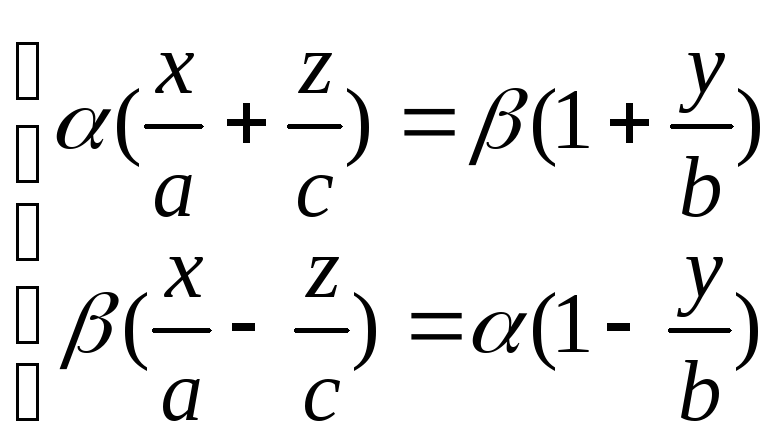где и - некоторые числа, не равные нулю одновременно. Если и фиксированы, то эти уравнения определяют прямую; меняя и , получим бесконечную систему прямых. Если перемножить эти уравнения почленно, то получим уравнение гиперболоида. Отсюда следует, что каждая из этих прямых целиком лежит на однополостном гиперболоиде.

Знаменитому русскому инженеру, почетному члену АН СССР Владимиру Григорьевичу Шухову принадлежит идея использования линейчатого характера однополостного гиперболоида в строительной технике. В.Г. Шухов предложил конструкцию из металлических балок, расположен-ных так, как расположены прямолинейные образующие однополостного гиперболоида (вращения). Такие конструкции оказались легкими и прочными. Они часто применяются для устройства водопроводных башен и высоких радиомачт (примером, может служить телевизионная башня на Шаболовской улице в Москве).

3.4. Поверхности вращения

Некоторые поверхности второго порядка могут быть образованы вращением плоской кривой вокруг одной из координатных осей. Линия называется меридианом поверхности вращения, а ось, вокруг которой вращается меридиан - осью вращения поверхности.

Так, конус

получается при вращении прямой (меридиан), расположенной в плоскости ОУZ, вокруг оси ОZ.

А двуполостный гиперболоид вращения

получается при вращении гиперболы

,

лежащей в плоскости ОУZ, вокруг оси ОZ.

При пересечении поверхностей вращения плоскостью, перпендикулярной к оси вращения, в сечении получаются окружности.

3.5. Основные поверхности второго порядка

Здесь мы рассмотрим некоторые поверхности второго порядка, заданные своими каноническими уравнениями и исследуем форму этих поверхностей, применяя метод параллельных сечений; этот метод позволяет определить форму поверхности по ее каноническому уравнению. Для этого рассматриваются линии пересечения поверхности с координатными плоскостями и плоскостями им параллельными. Так, если в уравнении поверхности положить (пересечь поверхность плоскостью, параллельной плоскости ОХУ), то получим уравнение линии пересечения . Меняя параметр , получим семейство линий пересечения, по виду которых достаточно хорошо можно представить вид исследуемой поверхности.

3.5.1. Эллипсоид

Эллипсоидом называют поверхность, каноническое уравнение которой имеет вид:

,

где - положительные числа, называемые полуосями эллипсоида.

Исследуем форму этой поверхности.

1. Координаты в каноническое уравнение входят во второй степени, следовательно, координатные плоскости являются плоскостями симметрии, а координатные оси – осями симметрии эллипсоида; заметим, что вместе с точкой поверхности принадлежит и точка , т.е. начало координат является центром симметрии поверхности – эллипсоид относится к центральным поверхностям.

2. Из канонического уравнения следует, что , , , или для всех точек эллипсоида, т.е. эллипсоид целиком располагается внутри параллелепипеда с ребрами , т.е. эллипсоид - ограниченная поверхность.

3. Применим метод параллельных сечений.

Рассмотрим сечение эллипсоида координатной плоскостью ОХУ (z=0) и плоскостями .

В сечении получатся эллипсы.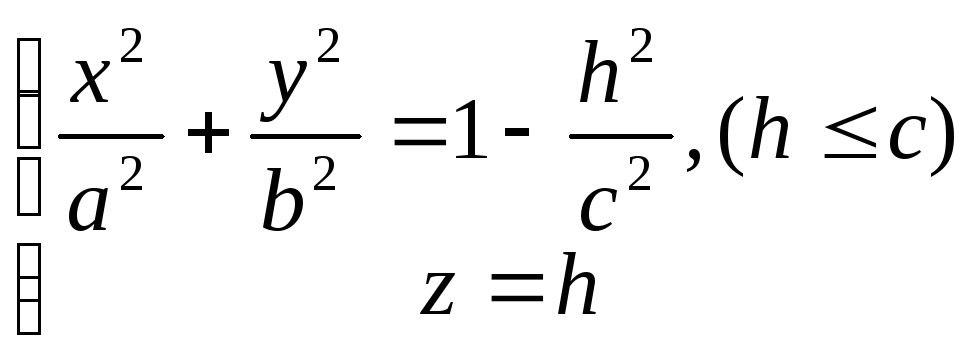

Полуоси эллипсов пересечения имеют наибольшие значения в плоскости ХОУ при h=0, при возрастании h значения убывают и обращаются в нуль при . Это означает, что плоскости имеют по одной общей точке с эллипсоидом, являются касательными плоскостями.

Аналогичные заключения можно сделать, рассекая эллипсоид плоскостями, параллельными ХОZ и УОZ. В частности, при пересечении эллипсоида плоскостями ХОZ (у=0) и УОZ (х=0) в сечении получаются эллипсы и . Суммируя проведенные исследования, приходим к выводу, что в данной системе координат эллипсоид имеет вид (рис. 10):

Рис. 10

Итак, эллипсоид есть замкнутая овальная поверхность, обладающая тремя взаимно перпендикулярными плоскостями симметрии.

Если полуоси эллипсоида различны, эллипсоид называется трехосным. Если же какие-либо две из величин одинаковы, например, = , тогда при пересечении с плоскостью получаются окружности с центром на оси OZ. Данный эллипсоид

является эллипсоидом вращения и получается при вращении эллипса вокруг оси OZ.

В случае, когда все полуоси равны = = получается сфера с центром в начале координат и радиусом .