
- •Дидактический план
- •Литература Основная
- •Дополнительная
- •Перечень умений
- •1.1.2. Векторное произведение
- •1.1.3. Смешанное произведение
- •1.2. Плоскость в пространстве
- •1.2.2. Общее уравнение плоскости. Неполное уравнение
- •1.2.3. Уравнение плоскости «в отрезках»
- •1.2.4. Угол между двумя плоскостями
- •1.2.5. Расстояние от точки до плоскости
- •2. Прямая в пространстве
- •2.1. Различные уравнения прямой
- •2.1.1. Прямая как пересечение двух неколлинеарных плоскостей
- •2.1.2. Угол между двумя прямыми
- •2.2. Прямая и плоскость в пространстве
- •2.3. Типовые задачи
- •3. Поверхности второго порядка
- •3.1. Общее уравнение второго порядка
- •3.2. Канонические уравнения второго порядка
- •3.3. Линейчатые поверхности
- •3.4. Поверхности вращения
- •3.5. Основные поверхности второго порядка
- •3.5.1. Эллипсоид
- •3.5.2. Однополостный гиперболоид
- •3.5.3. Двуполостный гиперболоид
- •3.5.4. Параболоиды
- •3.5.5. Конус
- •3.5.6. Цилиндры второго порядка
- •Приложения
- •1. Понятие линейного пространства
- •2. Понятие линейного функционала
- •3. Гиперплоскость в пространстве Rn
- •4. Уравнение прямой в произвольном линейном пространстве Rn
- •Задания для самостоятельной работы
- •1. Составьте логическую схему базы знаний по теме юниты:
- •2. Решите самостоятельно следующие задачи: Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Тренинг умений
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Пример выполнения упражнения тренинга на умение 1б Задание
- •Решение
- •Выполните самостоятельно следующие задания: Задание 1
- •Глоссарий
3.5.4. Параболоиды
Пусть уравнение
второго порядка приведено к каноническому
виду
![]() ,
,
![]() ,
,
![]() .
Поверхности, заданные этими уравнениями,
называют параболоидами.
.
Поверхности, заданные этими уравнениями,
называют параболоидами.
У равнение
равнение
![]() определяет эллиптический параболоид.
Исследуя форму этой поверхности методом
параллельных сечений, можно убедиться,
что в сечении плоскостями, параллельными
координатным, получаются либо параболы,
либо эллипсы (отсюда и название
поверхности). Таким образом поверхность
имеет вид бесконечной выпуклой чаши с
двумя взаимно перпендикулярными
плоскостями симметрии, проходящими
через начало координат (рис. 13).
определяет эллиптический параболоид.
Исследуя форму этой поверхности методом
параллельных сечений, можно убедиться,
что в сечении плоскостями, параллельными
координатным, получаются либо параболы,
либо эллипсы (отсюда и название
поверхности). Таким образом поверхность
имеет вид бесконечной выпуклой чаши с
двумя взаимно перпендикулярными
плоскостями симметрии, проходящими
через начало координат (рис. 13).
Э
Рис. 13
![]() вокруг оси Oz, имеет
уравнение:
вокруг оси Oz, имеет
уравнение:
![]() и является
параболоидом вращения.
и является
параболоидом вращения.
Гиперболический параболоид задается уравнением:
![]() ,
,
![]() ,
,
![]() .
.
В сечении этого гиперболоида плоскостями, параллельными координатным, получаются гиперболы и параболы (что и определяет название поверхности). Эта поверхность имеет форму седла (рис. 14). Гиперболический параболоид имеет две взаимно перпендикулярные плоскости симметрии, совпадающие с координатными плоскостями y = 0 (XOZ) и x = 0 (YOZ). Начало координат – вершина параболоида является ее «седловой» точкой».
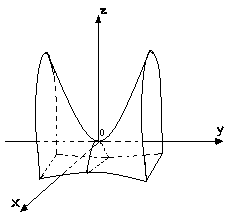
Рис. 14
3.5.5. Конус
Поверхность, которая в некоторой системе координат определяется уравнением:
![]()
называется конусом второго порядка.
О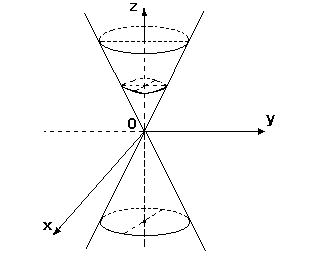 собенностью
этого уравнения является то, что оно
однородно, т.е. все его члены имеют одну
и ту же степень (равную двум). Отсюда
следует геометрическая особенность
поверхности: если некоторая точка M
(отличная от начала координат) лежит на
этой поверхности, то все точки прямой,
проходящей через начало координат и
точку М, также лежат на этой поверхности.
Тем же свойством обладают все поверхности,
которые в декартовых координатах
определяются однородным уравнением.
Итак, поверхность, определяемая однородным
уравнением, состоит из прямых,
проходящих через одну точку (начало
координат). Такая поверхность называется
конической, или, просто конусом.
Прямые, из которых составлен конус,
называются его образующими, точка,
через которую все они проходят, называется
вершиной конуса.
собенностью
этого уравнения является то, что оно
однородно, т.е. все его члены имеют одну
и ту же степень (равную двум). Отсюда
следует геометрическая особенность
поверхности: если некоторая точка M
(отличная от начала координат) лежит на
этой поверхности, то все точки прямой,
проходящей через начало координат и
точку М, также лежат на этой поверхности.
Тем же свойством обладают все поверхности,
которые в декартовых координатах
определяются однородным уравнением.
Итак, поверхность, определяемая однородным
уравнением, состоит из прямых,
проходящих через одну точку (начало
координат). Такая поверхность называется
конической, или, просто конусом.
Прямые, из которых составлен конус,
называются его образующими, точка,
через которую все они проходят, называется
вершиной конуса.
Форму конуса можно исследовать, как и раньше, методом параллельных сечений (15).
В случае
![]() =
=
![]() в уравнении конуса
в уравнении конуса
![]() ,
,
п
Рис. 15
3.5.6. Цилиндры второго порядка
В заключение обзора поверхностей второго порядка отметим еще случай, когда в уравнении отсутствует какая-нибудь координата. Такое уравнение определяет цилиндрическую поверхность второго порядка (или цилиндр) с образующими, параллельными той оси, координата которой в уравнении отсутствует.
Так, поверхность, заданная уравнением
![]() ,
,
является цилиндром с образующими, параллельными оси OY. Сечением цилиндра плоскостью XOZ является окружность с центром в начале координат и радиусом, равным единице (рис. 16). Заметим, что уравнение цилиндра не отличается от уравнения окружности, называемой направляющей для данного цилиндра.
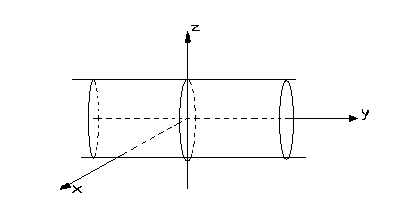
Рис. 16
Среди цилиндров, образующие которых параллельны оси OZ различают цилиндры следующих типов:
а) эллиптический цилиндр
![]() ;
;
при
![]() =
=
![]() ,
получается круговой цилиндр
,
получается круговой цилиндр
![]() ;
;
б) гиперболический цилиндр
![]() ;
;
в) параболические цилиндры
![]() или
или
![]() .
.
Тип цилиндра зависит от вида направляющей цилиндра в плоскости XOY (рис. 17)
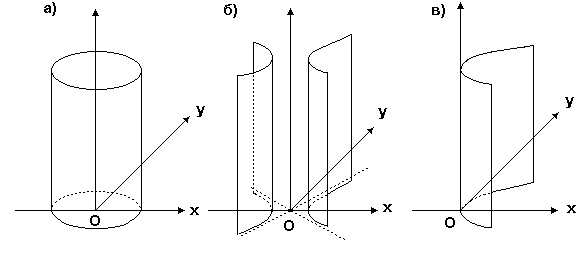
Рис. 17
