1.2.2. Линеаризация сау

В общем случае САУ нелинейны, т.е. хотя бы в одном звене имеется нелинейная характеристика. Решение дифференциальных уравнений нелинейного вида типа (1.2.3) представляет большую трудность. Поэтому необходимо произвести линеаризацию нелинейных характеристик реальных звеньев.

Линеаризацией называют замену нелинейного уравнения Y=f(t) приближенно линейным YKX.

Основой линеаризации является выдвинутое П.А. Вышнеградским предложение, что в течение всего процесса управления имеют место достаточно малые отклонения всех переменных от их установившегося значения. Это дает возможность линеаризовать нелинейную функцию в окрестности точки установившегося равновесия. Такую линеаризацию осуществляют методом А.М. Ляпунова. Линеаризацию по Ляпунову проводят в окрестности установившегося состояния с последующим отбрасыванием нелинейного остатка разложения Х.

Разложим непрерывную нелинейную функцию f(X) в ряд Тейлора

(1.2.5)

Если ограничиться первым приближением линеаризации, то получим линейное уравнение относительно X

, (1.2.6)

где - угол наклона зависимости в точке X₀(рис.1.2.1).

Рис.1.2.1. Линеаризация дифференциальных уравнений САУ

Часто уравнения нужно записывать в приращениях:

f(X)=f₀(X₀)+f(X) или

. (1.2.7)

Для того, чтобы привести уравнения к единому безразмерному виду, проводят нормирование и получают уравнения в относительных единицах. Нормирование осуществляют путем деления на базовое значение или номинальную величину . В этом случае эти величины можно сравнивать качественно и количественно.

1.2.3. Решение дифференциальных уравнений сау

Линеаризация и приведение к типовой форме дают временное уравнение динамики системы в общем виде

, (1.2.8)

где a₀, a₁,...a_n-1, a_n- коэффициенты при производных выходного параметра Y;

b₀,...b_m-1, b_m- коэффициенты при производных входного параметра.

Классический метод решения уравнения (1.2.8) заключается в получении аналитического выражения общего интеграла уравнения, который определяется суммой

Y(t) = Y_вын + Y_св(t), (1.2.9)

где Y(t) - общее решение, дающее переходной процесс выходной величины в функции времени;

Y_вын- частное решение уравнения, определяющее вынужденное (установившееся) движение для производных равных нулю;

Y_св(t) - решение левой части уравнения (1.2.8), приравненное нулю (характеризует свободное движение).

В частном случае, когда корни характеристического уравнения _iвещественные для характеристического уравнения

, (1.2.10)

получим

, (1.2.11)

где C_i- постоянные интегрирования,_i- корни характеристического уравнения (1.2.10).

Если корни _iмнимые, то в решении (1.2.11) будут и гармонические составляющие, т.е. будет происходить колебательный процесс.

1.2.4. Преобразование Лапласа

Для решения дифференциальных линейных уравнений удобно использовать операторный метод, при котором функции времени по определенным правилам заменяются соответствующими им операторными изображениями; по ним проводят решение, а затем переходят от изображений к самим значениям.

Операторным изображением какой-либо функции времени f(t), которую называют оригиналом, является функция F(P) комплексной переменной P=C+j, связанная с ней преобразованием Лапласа:

; (1.2.12)

, (1.2.13)

где P - оператор Лапласа, - знак изображения по Лапласу, C - реальная часть,- мнимая часть.

Для получения изображения дифференциального уравнения в ТАУ чаще используют преобразование Карсона

, (1.2.14)

где К - знак преобразования Карсона, отличающийся от знака по Лапласу умножением его на оператор Р.

Соответствующие преобразования

(1.2.15)

вычислены и сведены в таблицы, которые следует использовать при анализе САР:

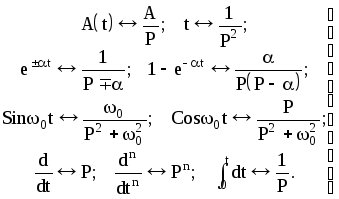(1.2.16)