Качество управления нелинейных систем.

Качество управления линейных систем характеризовалось временем регулирования t_p, перерегулированием , временем нарастания t_н, временем достижения максимума t_max, затуханием , числом колебаний за время регулирования n, периодом колебаний и т. д. Все показатели можно было определить прямым методом, т. е. по переходному процессу.

Аналогичный прием допускается для нелинейных систем. Однако, существуют некоторые особенности. Суть их в заключается в следующем:

Для линейных систем допускалось построить переходный процесс или реакцию на ступеньку, т. е. на 1(t). Все остальные переходные процессы имели такую же форму с масштабным коэффициентом к. Для нелинейных систем реакция на входное воздействие зависит от амплитуды воздействия. При малых амплитудах переходный процесс может затухать, а при больших расходиться и наоборот. Поэтому для нелинейных систем необходимо построить семейство переходных процессов для разных входных воздействий. При определении параметров, характеризующих качество, необходимо указать для какого воздействия они получены.

Анализ качества управления по логарифмическим характеристикам

Качественно выполнить анализ качества управления системы можно по логарифмическим характеристикам. Рассмотрим применение метода для частных случаев. Пусть исходное нелинейное звено имеет зону нечувствительности. Будем считать амплитуду внешнего воздействия А=х<а. При этом характеристика является линейной, поэтому логарифмическая характеристика системы, содержащая такую нелинейность, будет очень близка к логарифмической характеристики линейной части.

Пусть амплитуда внешнего воздействия уменьшается и становится х<a, при этом коэффициент гармонической линеаризации к_Г эквивалентной передаточной функции звена изменяется в соответствии со следующим рисунком.

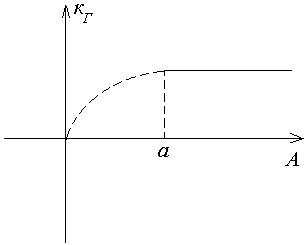
При А<а коэффициент уменьшается, следовательно уменьшается коэффициент передачи системы в целом и логарифмические характеристики L₁, L₂ и т. д. будут располагаться ниже. Из рисунка частота среза при уменьшении амплитуды входного воздействия начинает уменьшаться, а период колебаний увеличиваться. Иначе нелинейное звено с зоной нечувствительности приводит к уменьшению быстродействия всей системы при малых входных воздействиях.

Пусть нелинейное звено в системе имеет зону нечувствительности и зону насыщения. Будем считать, что амплитуда входного воздействия А=х на нелинейный элемент удовлетворяет условию ха. При этом характеристика имеет участок с постоянным наклоном и коэффициент к_нл= к_Г, тогда при таких условиях систему в целом можно считать линейной и логарифмические характеристики будут очень близки к логарифмическим характеристикам эквивалентной системы.

Б удем увеличивать амплитуду входного воздействия. При ха начинает сказываться нелинейность при этом коэффициент к_Г начинает уменьшаться в соответствии с графиком.

В результате коэффициент передачи всей системы уменьшится, поэтому при увеличении х логарифмические характеристики системы будут располагаться ниже L. Из логарифмической характеристики следует: при увеличении входного воздействия частота среза системы уменьшается, уменьшается быстродействие, уменьшается запас устойчивости , увеличивается период колебаний.

Из 2х рассмотренных примеров следует:

1. Нелинейное звено в системе затягивает переходный процесс

2. Звено с насыщением затягивает переходный процесс при больших воздействиях, а звено с зоной чувствительности при малых.

Сказанное иллюстрируется следующим рисунком.

Анализ качества управления нелинейной системы на основе гармонической линеаризации

Пусть нелинейная система сводится к виду.

Будем считать, что выполняется условие фильтра и допустима гармоническая линеаризация. Предположим, что процесс в системе затухает и затухание характеризуется коэффициентом  при частоте . Для затухающих колебаний условие фильтра сохраняется. В результате гармонической линеаризации звено F(z) сведем к линейному W_нл(р). Для большинства систем передаточные функции есть рациональная дробь вида

, тогда для разомкнутой системы 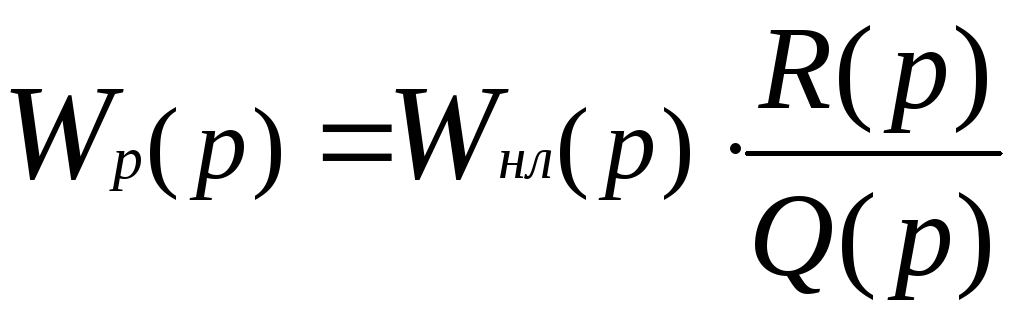(1)

для замкнутой системы (2)

Знаменатель выражения (2) определяет характеристический полином D_з(p) замкнутой системы D_з(p)=Q(p)+(к_Г+ к’_Гр/)R(p) (4)

Выполним для (4) преобразование Лапласа, заменяя р на s, где s=+j

D_з(+j)=Q(+j)+(к_Г+ к’_Г(+j)/)R(+j)

Коэффициенты к_Г и к’_Г являются функциями амплитуды колебаний, т. е. к_Г= к_Г(А), к’_Г= к’_Г(А)

D_з(+j)= Q(+j)+ к_Г(А) R(+j)+ к’_Г(A)(+j)/) R(+j) (5)

Выражение (5) является комплексным и после приведения подобных членов может быть приведено к виду D_з(+j)=X(,,A)+jY(,,A) (6)

Перейдем от характеристического уравнения к характеристическому уравнению D_з(+j)=0. Это возможно при X(,,A) (7)

Y(,,A)

Система (7) имеет 2 уравнения и 3 неизвестных параметра, поэтому решение может быть найдено в следующем виде =(А), =(А). Полученный результат совпадает с выводами предыдущего вопроса (иллюстрации те же). Конкретный вид аналогичной зависимости может быть получен при заданном характеристическом уравнении.

Анализ качества управления по косвенным признакам

Определение показателей качества по переходному процессу называют прямым методом. В ряде случаев переходный процесс можно не строить, а показатели качества получит косвенно.

Пусть нелинейная система исследовалась по Ляпунову и при этом получено

lim x(t)=0, где x(t) выходная координата. В этом случае переходный процесс в нелинейной системе предлагается сравнивать с переходным процессом в линейной системе, проходящей по экспоненте е^-t. Для экспоненты lim е^-t=0. Поэтому lim x(t) е^-t=0 (1). Значение  будем плавно изменять при это можно найти такое значение , изменение которого приводит к нарушению условия (1). Тогда  косвенно характеризует затухание в нелинейной системе x(t) и оно имеет тот же порядок, что и затухание в линейной системе. Для линейной системы было получено t_p=3/, значит время регулирования в нелинейной системе имеет тот же порядок. Здесь  есть степень устойчивости и определяется расстоянием от ближайшего левого корня до мнимой оси.