1.6.2. Корневой критерий устойчивости

Итак, условием затухания переходных процессов и устойчивости САУ является отрицательность вещественной части корней

_i<0 в_i=_i j. (1.6.9)

Если корни рассмотреть на комплексной плоскости (рис.1.6.2), то необходимым и достаточным условием устойчивости будет расположение корней в левой полуплоскости. Это классический критерий устойчивости.

1.6.3. Алгебраический критерий устойчивости

Вычисление корней характеристического уравнения затруднено. Поэтому были выведены критерии устойчивости, позволяющие судить об устойчивости системы непосредственно по коэффициентам характеристического уравнения без вычисления корней.

Характеристическое уравнение (1.2.10) можно представить в виде сомножителей

a₀(-₁)(-₂)...(-_i)...(-_n)=0, (1.6.10)

где _i- корни характеристического уравнения.

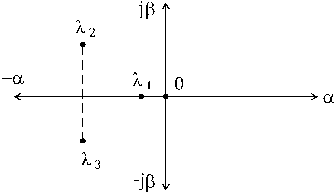
Рис. 1.6.2. Коневой критерий устойчивости

Для устойчивости системы _i<0, т.е._i=-_i.

При этом получим

a₁(+₁)(+₂)...(+_n)=0. (1.6.11)

При перемножении членов уравнения (1.6.11) коэффициенты перед в алгебраическом уравнении вида (1.6.6) будут положительными:

a₀>0; a₁>0;...a_n>0. (1.6.12)

Для случая с комплексными корнями это условие выполняется только для уравнений 2-го порядка.

Для САУ, описываемой уравнением 1 и 2 порядка, алгебраическим критерием устойчивости является положительность всех коэффициентов уравнения a_i>0. Для других САУ это условие является необходимым.

1.6.4. Критерий устойчивости Гурвица

Алгебраический критерий устойчивости работает только на САУ 1 и 2-го порядка.

Для САУ более высокого порядка применяется критерий устойчивости Гурвица.

Для устойчивости системы необходимо и достаточно, чтобы были положительными главные определители Гурвица, составленные из квадратной матрицы коэффициентов характеристического уравнения.

Правило составления определителей Гурвица следующее:

1. По диагонали матрицы от левого верхнего угла до правого нижнего угла записываются все коэффициенты характеристического уравнения САУ от a₁до a_n.

2. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента, а также если индекс его меньше нуля или больше n, на месте его пишется нуль.

3. Из матрицы выбираются диагональные миноры и они являются определителями Гурвица.

a1	a3	a5	.	. .	0	0
a0	a2	a4	.	. .	0	0
0	a1	a3	.	. .	0	0
0	a0	a2	.	. .	0	0	. (1.6.13)
. .	. .	. .	.	. .	.	.
0	0	0	.	. .	an-1	0
0	0	0	.	. .	an-2	an

Указанные определители Гурвица имеют вид:

... (1.6.14)

Пример. Рассмотрим устойчивость замкнутой системы (1.5.5) с передаточной функцией разомкнутой системы (рис.1.6.3).

.

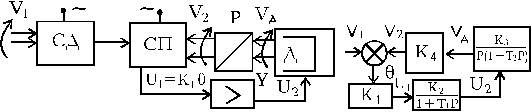
Рис.1.6.3. Система дистанционного слежения: СД - сельсин-датчик; СП - сельсин-приемник; Р - редуктор; Д - двигатель; У - усилитель

Характеристическое уравнение замкнутой системы имеет третий порядок

1+W(P)=0, T₁T₂P³+(T₁+T₂)P²+P+K=a₀P³+a₁P²+a₂P+a₃=0. (1.6.15)

Определитель Гурвица будет иметь вид:

(1.6.16)

или

. (1.6.17)

Для K=80, T₁=0,12c, T₂=0,05c условие (1.6.17) не выполняется - система неустойчива. Для данных T₁и T₂система устойчива при K=K_кр=28.