1.5.5. Построение логарифмических частотных характеристик сау

Применение логарифмических частотных характеристик имеет ряд преимуществ. Логарифмический масштаб позволяет наглядно изобразить их ход в большом диапазоне изменения частот и уменьшает кривизну настолько, что становится возможным представлять характеристики с малой погрешностью в виде асимптотических ломаных линий. Характеристики звеньев системы имеют простую стандартную форму в виде отрезков прямой линии. Характеристика системы получается как сумма характеристик звеньев простым графическим сложением их наклона по участкам. По логарифмическим характеристикам легко оценить устойчивость и качество системы, наглядно видно, как система реагирует на любые изменения своей структуры и параметров.

И самое важное преимущество метода логарифмических частотных характеристик состоит в том, что он, по сравнению с другими методами, наиболее разработан. Большое число разработанных таблиц, номограмм, шаблонов по расчету позволяет назвать этот метод инженерным.

Насколько просто построить ЛЧХ убедимся на примере построения их для разомкнутой следящей системы автоматической ориентации электрода относительно свариваемого стыка, описываемой передаточной функцией

, (1.5.5)

где К=80; T₁=0,12c; T₂=0,05c.

Отсюда

.(1.5.6)

Порядок построения ЛАЧХ по виду и параметрам (рис.1.5.5).

1. Устанавливаем масштабы для осей ординат L() и абсцисс lg().

Первая составляющая не зависит от частоты и проходит на уровне 20lgK = 201,92 = 38,4 дБ.

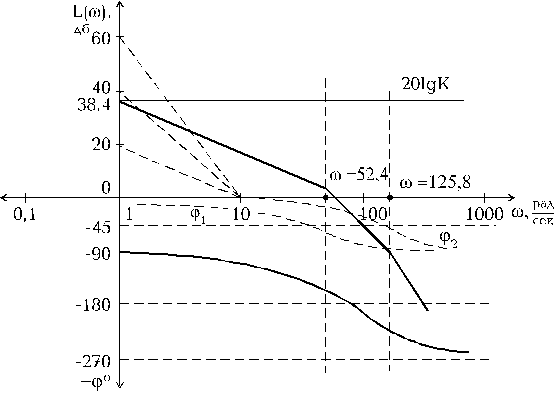
Рис.1.5.5. Построение логарифмических частотных характеристик САУ

2. Определяем частоты всех постоянных времени

₁=2/T₁=52,4 рад/сек,₂=2/T₂=125,8 рад/сек. Через отложенные на оси абсцисс частоты сопряжения проводятся вертикальные линии.

3. При =1 (lg=0) откладываем ординату 20lgК =38,4 дБ.

4. Через точку 20lgК, =1 проводим прямую с наклоном - 20 дБ/дек до пересечения с вертикалью наименьшей частоты сопряжения, т.е. до первой вертикали от оси ординат L(). Это есть первая (низкочастотная) асимптота ЛАЧХ. Для случая 20lg= 0 она превращается в горизонтальную линию.

5. Проведем вторую асимптоту от конца первой до пересечения с вертикалью второй по величине сопрягаемой частоты. Ее наклон меняется еще на -20 дБ/дек, т.е. составляет - 40 дБ/дек.

6. Строим еще одну асимптоту от конца второй с наклоном уже - 60 дБ/дек.

7. Если сомножитель числителя и знаменателя имеет исходную характеристику колебательного характера, то асимптотическая характеристика должна быть скорректирована в окрестности сопрягаемой частоты для оператора типа T₁T₂P²+T₂P+1.

Логарифмическая фазочастотная характеристика строится обычным методом при сложении по составляющим фаз звеньев графическим путем:

(1.5.7)

При сложных зависимостях кривые ЛАЧХ и ЛФЧХ легче рассчитать на персональной ЭВМ.

1.6. Устойчивость сау

1.6.1. Понятие об устойчивости и виды устойчивости

Основным динамическим свойством САУ является ее устойчивость. Устойчивостью называется свойство системы возвращаться в исходное или новое установившееся состояние после всякого выхода из него в результате внешнего воздействия (рис.1.6.1). Неустойчивые системы разрушаются, они неработоспособны. Поэтому актуальнейшей инженерной задачей является проверка САУ на устойчивость и обеспечение ее устойчивости.

Устойчивость системы необходимо исследовать в следующих случаях: при определении структуры САУ, при выборе параметров звеньев, при настройке и выборе допустимых пределов изменения параметров.

Устойчивость линейной системы не зависит от величины возмущения. Доказано Ляпуновым, что линейная динамическая системы, устойчивая при малых возмущениях, будет устойчивой и при больших возмущениях. Поэтому для суждения об устойчивости САУ достаточно определить устойчивость в "целом" по передаточной функции системы. Так как передаточная функция представляется в виде (1.2.8) и (1.2.17):

, (1.6.1)

где К - коэффициент; a₀, a₁,... a_n- коэффициенты полинома выходного параметра; b₀, b₁,... b_n- коэффициенты полинома входного воздействия;- оператор дифференцирования.

Отсюда видно, что математическая модель САУ представляется в виде параметрического и дифференциального уравнений:

(a₀Pⁿ+ a₁P^n-1+...+a_n-1P+a_n)Y(t)=(b₀P^m+b₁P^m-1+...+b_m-1P+b_m)X(t) (1.6.2)

или

(1.6.3)

Мы уже ознакомились с решением дифференциальных уравнений (1.2.8)...(1.2.11), т.е. Y(t)=Y_вын.+Y_св(t),

где Y_вын.- частное решение уравнения, определяющее вынужденное движение для производных равных нулю;

Y_св(t) - решение левой части уравнения, приравненное нулю (свободная составляющая).

Считают, что САУ устойчива, если свободная составляющая будет затухать, т.е.

. (1.6.4)

Свободная составляющая представляется в решении уравнения (1.6.3) следующим видом:

, (1.6.5)

где _i- корни характеристического уравнения, полученного из левой части уравнения (1.6.2) или (1.6.3):

a₀ⁿ+a₁^n-1+...+a_n-1+a_n=0. (1.6.6)

Решение характеристического уравнения зависит от его корней, которые в общем виде могут быть комплексными

_i =_i j_i. (1.6.7)

Рассмотрим лишь две составляющие процесса от пары сопряженных комплексных корней

Y_св(t)=c_ie^{(i+ji)t}+c_i+1e^{(i-ji)t}=, (1.6.8)

где c_i, c_i+1,- постоянные коэффициенты;

_i- частота колебаний;

_i- коэффициент затухания;

_i- фаза колебаний.

Анализ (1.6.8) показывает, что это синусоида с амплитудой, изменяющейся по экспоненте . Поэтому, если:

1) _i<0, e^itуменьшается при t, колебание затухает и САУ устойчива (рис.1.6.1,а,б);

2) _i>0, e^itувеличивается при t, колебание увеличивается и САУ неустойчивая (рис.1.6.1,д);

3) _i=0 - незатухающие колебания и САУ на границе устойчивости (рис.1.6.1,а);

4) _i=0 - процесс апериодический (рис.1.6.1,в).

Результаты анализа и виды устойчивости показаны на рис.1.6.1.

Рис.1.6.1. Переходные процессы устойчивых (а,б,в) и неустойчивых (г,д) САУ