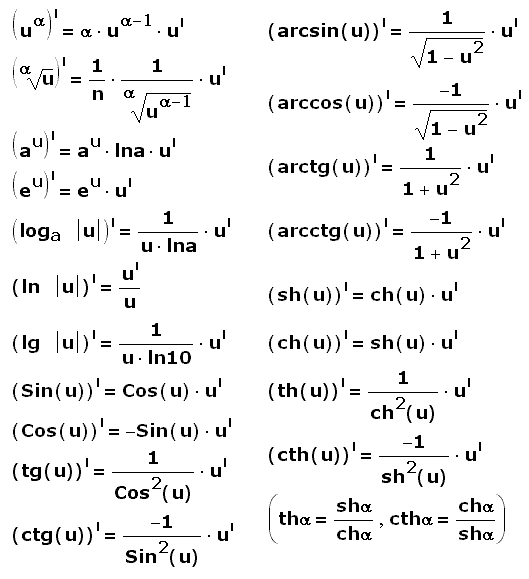- •I. Введение в анализ.
- •Предел функции в точке и на бесконечности. Геометрическая интерпретация. Теорема о единственности предела.
- •Бесконечно малые и бесконечно большие функции, их свойства
- •Теорема о связи функции с её пределом в точке
- •Алгебраические свойства пределов
- •Первый замечательный предел
- •Понятие предела последовательности. Теорема существования предела последовательности
- •Сравнение функций.
- •8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентности
- •9. Понятие непрерывной функции в точке. Свойства непрерывных в точке функций
- •Свойства Локальные
- •Глобальные
- •10.Односторонние пределы функции в точке. Точки разрыва и их классификация.
- •Односторонний предел по Гейне
- •11.Основные теоремы о непрерывных на отрезке функциях
- •11. Дифференциальное исчисление функций одной перемен-
- •Правила дифференцирования функций
- •Производная сложной, обратной, параметрически заданной функции
- •Понятие дифференциала функции и его геометрический смысл. Применение дифференциала к приближенным вычислениям
- •Основные теоремы о дифференцируемых функциях (т.Ролля, Лагранжа, Коши)
- •Производные и дифференциалы высших порядков
- •Правило Лопиталя раскрытия неопределенностей. Раскрытие показательных неопределенностей
- •Формула Тейлора с остаточным членом в форме Лагранжа и Пеано
- •Разложение основных функций по формуле Тейлора
- •Монотонные функции. Признаки возрастания (убывания) функции на интервале
- •Понятие экстремума функции в точке. Необходимое и достаточное условия экс тремума функции в точке
- •Исследование функций на экстремум с помощью высших производных
- •Наибольшее и наименьшее значения функции на отрезке
- •Выпуклость и вогнутость графика функции, точка перегиба. Необходимое и достаточное условия точки перегиба графика функции
- •Понятие асимптоты графика функции. Нахождение вертикальных и наклонных асимптот
- •Полное исследование функции и построение графика функции
- •III. Неопределенный интеграл.
- •Понятие первообразной и ее свойства. Теорема о множестве первообразных
- •30.Таблица неопределенных интегралов основных функций
- •Интегрирование по частям и заменой переменной в неопределенном интеграле
- •Интегрирование функций с квадратным трехчленом в знаменателе
- •Интегрирование рациональных дробей методом разложения на простые дроби
- •Рекуррентные формулы. Вычисление интеграла
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций. Универсальная подстановка. Некоторые частные случаи
- •1.4 Интегрирование тригонометрических функций.
- •37.Интегралы, содержащие квадратичную иррациональность, и их вычисление с помощью тригонометрических подстановок
- •IV. Определенный интеграл.
- •Понятие определенного интеграла, его геометрический смысл, свойства
- •Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница
- •Интегрирование по частям и заменой переменной в определенном интеграле
- •Для неопределённого интеграла
- •Для определённого
- •Несобственные интегралы I и п рода. Определение, свойства, теоремы сравнения
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •Несобственные интегралы II рода
- •Геометрический смысл несобственных интегралов II рода
- •Геометрические приложения определенного интеграла:
- •43. Физические приложения определенного интеграла (работа переменной силы при прямолинейном перемещении материальной точки, давление жидкости на пластинку).
- •V. Функции многих переменных.
- •44. Функции многих переменных (фмп). Область определения, предел в точке, непрерывность
- •2. Предел функции.
- •Понятие частной производной фмп. Правила дифференцирования
- •Дифференцирование сложной функции многих переменных. Формула для производной неявно заданной функции одной переменной
- •Касательная плоскость и нормаль к поверхности
- •Частный и полный дифференциалы фмп. Применение дифференциала к приближенным вычислениям
- •Частные производные высших порядков. Теорема о равенстве смешанных производных
- •Дифференциалы высших порядков
- •Формула Тейлора для функции двух переменных
- •Различные формы остаточного члена
- •Экстремумы фмп. Необходимое и достаточное условия экстремума фмп в точке
- •Постановка задач на экстремум. Нахождение наибольшего и наименьшего значений функции в замкнутой области
-
Производная сложной, обратной, параметрически заданной функции
Приведем правило по которому можно найти производную сложной функции y = f((t)).
Теорема 3 (дифференцирование сложной функции). Пусть функция x = (t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = (t). Тогда сложная функция y = f((t)) дифференцируема в точке t, причем справедлива формула
|
(f((t)))' = f'(x)'(t). |
(3) |
Доказательство. Зададим x = (t) отличное от нуля приращение t. Этому приращению отвечает приращение x = (t+ t)- (t) функции x = (t). Приращению x отвечает приращение y = f(x+ x)-f(x). Так как функция y = f(x) дифференцируема, то ее приращение y представимо в виде (1):
y =f'(x) x + ( x) x,
где lim x 0 ( x ) = 0. Поделив данное выражение на t 0, будем иметь:
y/ t=f'(x) x/ t+ ( x) x/ t.
Из дифференцируемости функции x = (t) в точке t вытекает, что
lim t 0 x/ t = '(t).Отметим, что из дифференцируемости функции x = (t) следует, что x 0 при t 0. Следовательно, lim t 0 ( x) =0. Таким образом, получим необходимую формулу (3).
Пример 5. Найти y', если y = 5cos x.
y' = 5cos x(-sin x)ln 5=-5cos x sin x ln 5.Для нахождения производной обратной функции существует следующее правило, а именно справедлива теорема
Теорема 4 (производная обратной функции). Пусть функция y = f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x. Пусть, кроме того, эта функция дифференцируема в точке x и f'(x) 0. Тогда в некоторой окрестности соответствующей точки y = f(x) определена обратная функция x = f-1(y), причем обратная функция дифференцируема в точке x = f-1(y) и для ее производной справедлива формула
(f-1(y))' = 1/f'(x).
Доказательство. Так как функция y = f(x) строго монотонна и непрерывна в некоторой окрестности точки x, то существует обратная функция x = f-1(y), которая является строго монотонной и непрерывной в некоторой окрестности точки y = f(x).
Пусть y 0 приращение для y, а x - соответствующее приращение обратной функции x = f-1(y). Тогда справедливо равенство
x/ y = 1/( y/ x).
Переходя к пределу в последнем равенстве при y 0 и учитывая, что в силу непрерывности обратной функции x 0, получим
lim y 0 x/ y = 1/ (lim x 0 y/ x).
То есть, x'(y) = 1/y'(x).
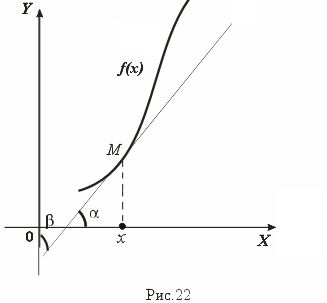
Доказанная теорема имеет простой геометрический смысл. Пусть M –точка графика функции f(x), (рис.22), производная f'(x) равна тангенсу угла наклона касательной, проходящей через M, к оси OX, а производная обратной функции (f-1(y))' в соответствующей точке y = f(x) равна тангенсу угла наклона той же самой касательной к оси OY. Так как углы наклона /2, то формула нахождения производной обратной функции выражает очевидный факт: tg = 1/tg .
Пример 6. Найти x'y, если y = 2x3+3x5+x Имеем y' = 6x2+15x4+1, тогда x'y = 1/y'x = 1/(6x2+15x4+1).
Пусть x = (t),y = (t), t [a,b] - достаточно гладкие функции. Тогда говорят, что функция задана параметрически. Примером параметрически заданной функции является уравнение окружности: x = acos t,y = asin t, t [0,2]. Рассмотрим вопрос о нахождении производных y = y(x) по переменной x.
В силу свойства инвариантности формы первого дифференциала следует, что y' = dy/dx, dy = '(t)dt, dx = '(t)dt. Поэтому
y'(x) = '(t)/'(t).
Используя формулу для второго дифференциала, получим
y(2)(x) = d(y'(x))/dx = ( '(t)/ '(t))'dt/ '(t)dt =
= ( ''(t) '(t)- ''(t) '(t))/( '(t))3.
Чтобы вычислить третью производную, запишем y'''(x) в следующем виде
y'''(x) = d(y''(x))/dx.
Пример 10. Функция задана параметрически
x = a(t-sin t), y = a(1-cos t).
Наити y''(x).
y't = asin t, x't = a(1-cos t).
Отсюда
y'(x) = (asin t)/(a(1-cos t)) = ctg (t/2), t 2 k.
y''(x) = d(ctg (t/2))/(a(1-cos t)) = -1/4sin4t/2. Пусть функция задана неявно уравнением F(x,y) = 0. Для нахождения производной функции, заданной неявно, нужно продифференцировать обе части уравнения, считая y = y(x) функцией от x, а затем из полученного уравнения найти производную y'. Чтобы найти производные высших порядков, нужно дифференцировать необходимое число раз уравнение F(x,y) = 0, и затем выразить нужную производную.
Пример 11. Найти y''(x), если :
x+y = ex-y. Дифференцируем данное уравнение по x, считая y функцией от x.
1+y'x(x) = ex-y(1-y'x(x)),откуда y'x = (ex-y-1)/(1+ex-y). Дифференцируя уравнение еще раз, получим
y''x(x) = ex-y(1-y'x(x))2-ex-yy''x(x), следовательно, y''x(x) = (1-y'x)2ex-y/(1+ex-y) = 4ex-y/(1+ex-y)3.
-
Таблица производных основных элементарных функций
(20 шт)