17. Исследование функций на экстремум с помощью высших производных

  Пусть в точке х = х₁ f(x₁) = 0 и f(x₁) существует и непрерывна в некоторой окрестности точки х₁.

  Теорема. Если f(x₁) = 0, то функция f(x) в точке х = х₁ имеет максимум, если f(x₁)<0 и минимум, если f(x₁)>0.

  Доказательство.

 Пусть f(x₁) = 0 и f(x₁)<0. Т.к. функция f(x) непрерывна, то f(x₁) будет отрицательной и в некоторой малой окрестности точки х₁.

Т.к. f(x) = (f(x)) < 0, то f(x) убывает на отрезке, содержащем точку х₁, но f(x₁)=0, т.е. f(x) > 0 при х<x₁ и f(x) < 0 при x>x₁. Это и означает, что при переходе через точку х = х₁ производная f(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.

Для случая минимума функции теорема доказывается аналогично.

Если f(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.

 

Выпуклость и вогнутость кривой. Точки перегиба.

  Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

 

 у

 

 

  На рисунке показана иллюстрация приведенного выше определения.

  Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).

 Доказательство. Пусть х₀  (a, b). Проведем касательную к кривой в этой точке.

  Уравнение кривой: y = f(x);

 Уравнение касательной:

Следует доказать, что .

 

По теореме Лагранжа для f(x) – f(x₀):  , x₀ < c < x.

 

По теореме Лагранжа для  

 

Пусть х > x₀ тогда x₀ < c₁ < c < x. Т.к. x – x₀ > 0 и c – x₀ > 0, и кроме того по условию

, следовательно, .

 

Пусть x < x₀ тогда x < c < c₁ < x₀ и x – x₀ < 0, c – x₀ < 0, т.к. по условию то

.

 

  Аналогично доказывается, что если f(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).

 

  Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

 Очевидно, что в точке перегиба касательная пересекает кривую.

 Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f(a) = 0 или f(a) не существует и при переходе через точку х = а f(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.

 Доказательство. 1) Пусть f(x) < 0 при х < a и f(x) > 0 при x > a. Тогда при

x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.

2)      Пусть f(x) > 0 при x < b и f(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.

25. Наибольшее и наименьшее значения функции на отрезке

 Решение многих задач практики приводит к отысканию наибольших или наименьших значений некоторой функции на некотором отрезке. Пусть, например, надо огородить проволокой данной длины  прямоугольный участок земли наибольшей площади. Если обозначить длину одной из сторон этого участка через , то длина другой стороны будет равна , а потому площадь участка равна . При этом  изменяется от  до  (при  и при  получаем «вырожденные» прямоугольники, одна из сторон которых имеет нулевую длину). Итак, надо найти значение x, при котором функция  при­нимает наибольшее значение на отрезке . Эту задачу можно решить элементарно,  записав выражение функции в  виде . Видим, что значение будет наибольшим, если . Выражение в этом случае равно . При  длина второй стороны тоже равна . Таким образом, наибольшую площадь среди прямоугольников  данного  периметра имеет квадрат.

Элементарные методы отыскания наибольших и наименьших значений функций применимы лишь для весьма узкого круга задач. Общий метод отыскания таких значений дает дифференциальное исчисление. Начнем с формулировки теоремы, гарантирующей существование таких значений.

Теорема 1. Если функция,  непрерывна на отрезке , то среди ее значений на этом отрезке есть наибольшее и наименьшее.

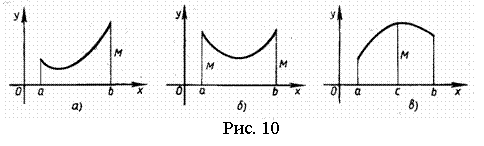
Теорема 1 дает лишь уверенность в существовании наибольших и наименьших значений непрерывной функции, но не указывает, как находить эти значения. Для наибольшего значения функции возможны два случая:

а) оно достигается на одном из концов отрезка  (рис. 10,а) или на обоих концах сразу (рис. 10,б).

б) оно достигается во внутренней точке  этого отрезка (рис. 10,в).

Во втором случае значение функции в точке  не меньше ее значений вблизи точки , и поэтому  - точка максимума (быть может, нестрогого) для . Но тогда в  либо функция  недифференцируема, либо ее производная равна нулю. Аналогично обстоит дело с наименьшим значением функции на отрезке .

Отсюда вытекает следующее правило отыскания наименьших и наибольших значений функции на отрезке:

Чтобы найти наименьшее и наибольшее значения непрерывной функции  на отрезке надо:

а) найти ее значения на концах, этого отрезка (т. е. числа  и );

б) найти ее значения в точках, где производная функции равна нулю;

в) найти ее значения в точках, где функция  не имеет производной;

г) из всех найденных значений выбрать наибольшее и наименьшее.

Подводя итог всему сказанному в этом пункте, замечаем, что задачи на наибольшие и наименьшие значения решаются по следующему плану:

1.  Выбирают одну из переменных (независимую переменную) и выражают через нее ту переменную, для которой ищется наибольшее или наименьшее значение. 2.  Находят промежуток изменения независимой переменной. 3.  Находят производную полученной в п.1 функции. 4.  Приравнивают производную нулю и находят корни получившегося уравнения. 5.  Находят точки, в которых функция не имеет производной. 6. Вычисляют значения функции на концах промежутка изменения независимой переменной и в точках, найденных в п.4 и 5, а потом выбирают из них наибольшее (соответственно наименьшее).

При этом для облегчения вычислений полезно иметь в виду следующие замечания:

1. Точка, в которой функция принимает наибольшее или наименьшее значение, не изменяется при следующих преобразованиях выражения, задающего функцию:

а) прибавлении постоянного слагаемого; б) умножении на отличное от нуля число (только при умножении на отрицательное число наибольшее значение переходит в наименьшее и обратно); в) возведении в степень с натуральным показателем, если функция неотрицательна.

2. Если положительная функция  принимает в точке а наибольшее (соответственно наименьшее) значение, то функции –   и  принимают в той же точке наименьшее (соответственно наибольшее) значение.